基于有限元技术的镍钛金属支架的优化设计

林 峰，刘祥坤，黄男男，高全超，李中华，姚天平，罗七一，黄嘉华

1 上海市医疗器械检测所，上海市，201321

2 上海微创医疗器械（集团）有限公司，上海市，201203

基于有限元技术的镍钛金属支架的优化设计

【作 者】林 峰1，刘祥坤2，黄男男2，高全超2，李中华2，姚天平1，罗七一2，黄嘉华1

1 上海市医疗器械检测所，上海市，201321

2 上海微创医疗器械（集团）有限公司，上海市，201203

利用有限元数值模拟方法分析了三种不同结构镍钛金属支架的力学性能及疲劳安全性。根据实际情况，提出合理的假设与简化条件，完成支架几何模型及有限元模型的创建、材料模型的选取及边界条件的设置。分析不同支架杆宽ω、棱角度θ对支架应变情况和疲劳安全性能的影响，为支架的优化设计提供有价值的参考。

镍钛金属支架；有限元分析；优化设计

目前，国内外支架市场前景广阔，对新支架的研究创新也在不断的进行。镍钛合金材料因其具有良好的机械性能和生物相容性，已被广泛地应用于该领域[1]。对于支架设计者来说，要想获得各方面性能优异的支架，必须经过一个从设计、加工到最后检验的过程，需要花费大量的时间与费用。

有限元分析技术能够直观的模拟出支架成型、压握进输送器、在人体血管内扩张等过程，可有效预测出不同过程中支架自身的变形、应力分布及血管内的疲劳安全性能。与一般不锈钢材料不同的是，镍钛合金材料具有独特的形状记忆效应和良好的超弹性，且镍钛金属支架的应变是其主要研究参数[2-3]。但支架在血管脉动和37 ℃体温的长期影响下力学性能下降,仍可能会发生疲劳破坏，这将导致一些严重的并发症,甚至直接威胁病人生命，Whitcher早在1997年就讨论了模拟结果对镍钛金属支架疲劳研究的意义[4-5]。基于有限元技术的支架分析结果，对其设计和优化具有较大的指导意义，不仅节省支架的研发时间，同时也提高临床安全性。本文介绍了基于有限元技术的镍钛金属支架优化设计方法，通过对比分析三种不同结构的支架分析结果，对支架设计提出指导意见。

1 有限元分析方法

1.1 支架材料属性模型

镍钛合金材料的关键特征是其超弹性，即在外力作用下因相变而产生远大于其弹性极限的应变，同时卸载后应变可自动回复的现象。在构建本构模型时，如何对这种高度非线性应力-应变行为进行合理描述，是保证有限元分析准确性的基础，也曾是众多研究者此前面对的难题[6]。本文的支架材料属性采用Abaqus软件中针对具有超弹性行为的记忆合金而开发的本构模型[7]。支架材料的应力-应变关系是通过对采用和实际工艺完全相同方法处理后的标准试件进行拉伸卸载实验后得到的。为验证镍钛合金材料模型的可靠性，在Abaqus中做单个单元的拉伸模拟，并将有限元模型得到的应力—应变曲线与实际测量的曲线作对比，结果显示两曲线十分吻合，如图1所示。由此说明Abauqs软件中形状记忆合金材料模型可以对镍钛合金复杂的应力—应变关系进行模拟。

图1中虚线是试验数据，黑色实线是拟合后得到的有限元分析时所使用的曲线。支架关键材料属性如表1（拉伸试验获得）所示。

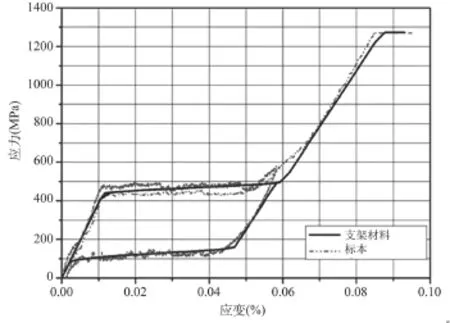
图1 支架材料应力—应变曲线Fig.1 Mechanical behavior of the Nitinol alloy

表1 支架材料属性表Tab.1 Material properties of Nitinol stent

1.2 有限元模型

本文分析的支架由镍钛合金管材切割而成，利用实体建模软件Solidworks建立的支架三维仿真模型如图2所示。支架的外径D0为6.1 mm，支架壁厚0.2 mm，长度L0为20 mm。采用三维实体单元C3D8I对支架几何模型进行离散化处理(网格化)，即可获得其有限元模型。如图2所示，支架单棱上符号分别代表：杆宽为ω、杆长为L、杆夹角为θ和壁厚为r。不同结构支架其单棱尺寸不一，具体尺寸见表2。

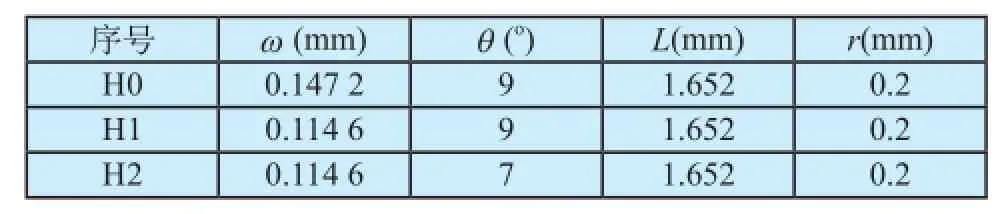
表2 支架单棱尺寸表Tab.2 Geometrical features of stents

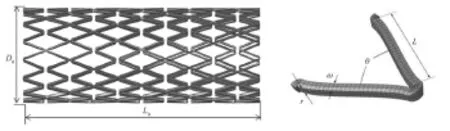
图2 支架几何模型图Fig.2 Finite element model of the Nitinol stent

为研究支架的整个使用过程，Lally C[8]建立了支架血管的简化模型。血管材料为超弹性材料模型，血管内径变化比值需满足血管顺应性的要求，本文中血管顺应性选取7%[9]，顺应性计算如式(1)。

其中，Dp1为p1压力下血管内径；Dp2为p2压力下血管内径；p1为低压值(舒张压)；p2为高压值(收缩压)。

1.3 分析过程及边界条件

镍钛金属支架具有其它材料支架所不具备的特殊性能，即可自扩张性。支架被压握进输送器后,经由大腿骨动脉或桡动脉输送到血管狭窄病变区，自行扩张到预定形状，支撑血管达到正常尺寸，从而达到治疗作用，手术结束后，支架长期留存在人体内发挥作用。因此，根据支架生产加工到介入人体的过程，按照三个不同结构支架不同压握、回弹及疲劳载荷情况条件，将分析过程分为以下三个步骤：(1)压握 模拟支架被压握过程，即利用压握工具将支架压到指定尺寸；(2)回弹 去除压握工具后，由于材料本身的特性，支架回弹到特定的形态；(3)疲劳分析 模拟支架在血管中，高压20 kPa与低压11 kPa交替循环变化过程中对支架的疲劳寿命影响[10-11]。

在模拟支架压握和压握回弹的过程中，利用一个圆柱形刚性管代替压握工具。对刚性管施加位移载荷，使支架从原始尺寸进行压握，一直到支架所要求的压握尺寸来模拟压握过程。然后去除刚性管，让支架自由回弹，来模拟支架的压握回弹过程。疲劳分析时，对血管内表面施加相当于平均生理血压的外载荷，来模拟支架在自身弹性以及血管压迫下的变化情况。

2 分析结果

2.1 压握后支架变形结果分析

支架的最大应变出现在压握进输送器后的状态，回弹过程则会释放大多数应变，因此支架压握后的应变分布情况是需要重点研究的。压握后的镍钛金属支架被固定在保护鞘内植入人体，此时支架的应变分布情况如图3所示。对比H0、H1和H2结构分析结果，可以看出，减小杆宽ω会增加支架压握应变；减小杆夹角θ角，支架在压握进输送器后，支架抗压能力增强，压握应变减小。

2.2 疲劳结果分析

支架在植入人体后与血管壁贴合，受到血管壁的作用力。在疲劳分析时，血管收缩和舒张对支架的影响，可通过对支架的外表面施加交替变化的作用力来模拟。支架疲劳性能的评判标准是根据Pelton等人提出的一种专门针对镍钛合金材料的研究结果[12]，如图4所示。图4中实线显示了302个样品经过107周期疲劳试验后得到的疲劳极限位置，反应了平均应力与交变应力的关系，若测试点分布在疲劳极限的曲线下方，说明支架在疲劳试验后，支架发生断裂的可能性不大；若测试点分布在曲线上方，则断裂极有可能发生，风险较大。此外，压应力对提高疲劳寿命是有利的[13]，所以，仅考虑拉应力对支架疲劳安全性能的影响。

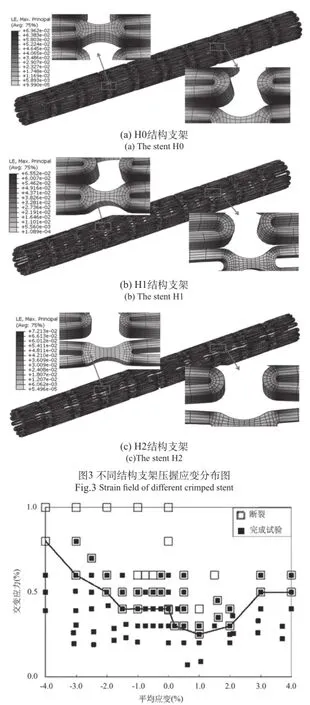
图4 Pelton疲劳图Fig.4 Fatigue diagram of Pelton

图5 不同结构支架疲劳图Fig.5 Alternating strain and mean strain of the different stent

在所有测试点的安全系数都大于1的情况下，其值越接近1，该点越靠近疲劳极限曲线，疲劳性能越差。因此，在有限元分析结果中，将把结构中距离疲劳线最近的测试点，即安全系数最小值，作为判断疲劳性能的重要参数。增加棱角度或是减小杆宽都会使支架的安全系数降低。支架平均应变和交变应变关系如图5所示，可以看出H0的疲劳图上测试点分布的位置在纵坐标方向相对最低，即疲劳安全性能最高。在整理分析结果时，通过导出支架的交变应变值，并计算出支架H0、H1和H2安全系数分别为6.51、5.01和5.44。结果表明，减小支架杆宽ω后，支架的疲劳性能明显降低；杆夹角θ减小时，支架的交变应变都会相应减小，一定程度上会提高支架的疲劳安全性能。

3 结论

本文利用有限元技术模拟了三种不同结构镍钛金属支架的整个使用过程，包括：压握、压握回弹和疲劳分析，通过这些过程分析支架的应变分布及其疲劳安全性能。3种支架变形过程都比较均匀，结果表明：支架被压握进输送器后，最大应变皆较小。对比H0、H1和H2结构分析结果，可以看出，减小杆宽ω会增加支架压握应变；减小杆夹角θ角，支架在压握进输送器后，支架抗压能力增强，压握应变减小。在各种工况都比较恶劣的情况下，三种不同结构支架的疲劳安全系数都大于1.00，处于安全范围。但减小支架杆宽ω后，支架的疲劳性能明显降低；杆夹角θ减小时，支架的交变应变都会相应减小，一定程度上会提高支架的疲劳安全性能。

可以看出，现有的有限元技术可以方便的对镍钛金属支架及其作用的生理环境进行模拟。通过对比分析最终结果，可以帮助设计人员较快的对其支架设计效果进行分析与评价，从而缩短设计周期，减少研发费用。

[1] Ted Feldman. Unique properties of self-expanding stents[J]. Catheteriz Cardiovasc Intervent , 2000, 49: 408-409.

[2] Stockel D, Pelton A, Duerig T. Self-expanding Nitionol stents: material and design considerations[J]. Eur Radiol, 2004, 14: 292-301.

[3] Duerig T, Pelton A, Stockel D. An overview of Nitinol medical applications. Mater Sci Eng, 1999, 149-160.

[4] Pelton AR, Schroeder V, Mitchell MR, et al. Fatigue and durability of Nitinol stents[J]. Mech Behav Biomed Mater, 2008,153-164.

[5] Whitcher FD. Simulations of in vivo loading condtions of nitinol vascular stent structures[J]. Comput Struct, 1997, 64:5-6.

[6] Petrini L, Dubini F, Dubini G, et al. Numerical analysis of vascular stents exploiting shape-memory-alloy behavior [C]. 16th AIMETA, 2003, 1-10.

[7] Abaqus Manual.Version 6.11 Dassault system[R]. [2011]. http:// www.simulia.com.

[8] Lally C, Dolan F, Prendergast PJ. Cardiovascular stent design and vessel stresses: a fi nite element analysis[J]. J Biomechanics, 2005, 38(8): 1574-1581.

[9] The British Standards Instiute. BS EN ISO 25539-1: 2009, Cardiovascular implants. Endovascular devices. Endovascular prostheses[S].

[10] The British standards Instiute. BS EN ISO 25539-2:2009, Cardiovascular implants Endovascular devices: Vascular stents[S].

[11] American Society for Testing and Materials. ASTM F2477-07 Standard test methods for in vitro pulsatile durability testing of vascular stents[S]. 2007.

[12] Pelton AR, Gong XY, Duerig T. Fatigue testing of diamond-shaped specimens[C]. Proc Confe Mater Process Med Devices, 2003, 199-204.

[13] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002.

Optimization Based on Finite Element Technique of Nitinol Stent

【 Writers 】Lin Feng1, Liu Xiangkun2, Huang Nannan2, Gao Quanchao2, Li Zhonghua2, Yao Tianping1, Luo Qiyi2, Huang Jiahua1
1 Shanghai Testing and Inspection Institute for Medical Devices, Shanghai, 201321
2 Shanghai MicroPort Medical (Group) Co., Ltd. Shanghai, 201203

nitinol stent, fi nite element analysis, optimization

R318.0

A

10.3969/j.issn.1671-7104.2014.02.005

1671-7104(2014)02-0098-04

2014-02-28

上海市科学技术委员会课题（11441900600）

黄嘉华，所长，高级工程师，E-mail: hjh85725@aliyun.com

【 Abstract 】The fi nite element method was used for simulating the mechanical performance and fatigue safety of three different structures of Nitinol stent. According to the actual situation, after proposing reasonable assumptions and simpli fi cation, the geometry model and fi nite element model establishment, material mode selection and boundary condition setting are completed. The strain and fatigue life of different stent edges wide (ω) or strut angle (θ) are computed. The result can provide a valuable reference for the optimal design of stent.