道路交通事故回归分析与预测

裘晨璐 季君 许卉莹 道路交通安全公安部重点实验室 公安部交通管理科学研究所

道路交通事故回归分析与预测

裘晨璐 季君 许卉莹 道路交通安全公安部重点实验室 公安部交通管理科学研究所

根据多元线性回归分析基本原理，以道路交通事故数据为研究基础，结合城市GDP、人口数、汽车保有量、城市道路长度、公路客运量、公路货运量六项影响因素，采取逐步进入策略，建立道路交通事故次数多元线性回归分析数学模型；结合显著性检验原理，给出了各因素导致道路交通事故发生的显著性作用评估方法，为合理有效地进行道路交通事故分析和预测提供了科学依据。

多元线性回归 事故预测

一、引言

一直以来，中国是世界上交通事故死亡人数最多的国家之一，每年都由此造成大量的人员伤亡和巨大的财产损失。为了有效控制和减少我国道路交通事故的发生，保障道路交通安全，开展一系列的交通安全方面的统计分析研究十分必要。其中基于回归分析的预测技术开展对区域安全状况分析及发展趋势预测的研究就是道路安全研究的重要方面[1-3]。本文采用多元线性回归方法，开展对影响道路交通安全趋势的相关因素分析，包括国民生产总值（GDP）、人口总数、汽车保有量、城市道路长度、公路客运量和公路货运量等，找出其主要影响因素及其关联性，建立交通事故预测回归模型，实现对区域内交通安全状况分析并预测其未来的发展趋势，从而为有针对性地、科学有效地制定合理的交通安全对策提供科学依据，这对于制定交通安全管理目标、提高交通安全管理水平具有十分重要的意义。本文还提出了对模型进行回归方程的显著性检验和回归系数的显著性检验方法。

二、多元线性回归基本原理

道路交通是一个涉及到多因素的复杂系统，一般与当地的经济发展水平、客观环境及人类社会活动有密切关系。交通事故虽然具有随机特性，但从统计的角度看，一个地区在较长时域内发生的交通事故又具有一定的规律性，因此可以运用数理统计方法对交通事故总体状况进行研究，分析其发展趋势及规律，科学地对道路交通事故进行预测。道路交通事故预测是通过对交通事故的过去和现在状态的系统探讨，并考虑其相关因素的变化所做出的对交通事故未来状态的描述过程。预测方法有多种，本文选择回归分析预测法[4]来进行预测分析。

回归分析是确定两种或两种以上变量间相互依赖定量关系的一种统计分析方法。在回归分析中，把变量分为两类，一类是因变量，代表实际问题中所关心的一些指标，通常Y用来表示；而影响因变量取值的另一类变量称为自变量，用X1,X2,…Xp来表示。当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性还是非线性，分为线性回归分析和非线性回归分析。通常线性回归分析法是最基本的分析方法，遇到非线性回归问题可以通过变量变换，将非线性回归化为线性回归，然后用线性回归方法处理[4]。回归分析的一般步骤如下：

1. 收集资料：通过调查分析，确定待研究变量可能的相关因素，并收集和处理这些因素的相关统计资料；

2. 相关性分析：对待研究目标和其影响因素作定性分析，确定是否存在相关关系；

3. 建立回归模型：选取相关度高的因素作为自变量建立回归分析模型，根据最小二乘法估计参数，求出回归方程；

4. 检验模型：在运用回归方程进行预测之前，对回归方程和回归系数进行显著性检验；

5. 利用模型进行预测：利用模型进行预测，并讨论预测结果的置信度。

（一）回归方程式

自变量为多个的线性回归称之为多元线性回归。设变量Y与变量X1,X2,…Xp间有线性关系，则多元线性回归方程式为[4]，

其中，β0是截距项，βj(j=1,2,…,p)为回归系数，p是自变量的个数，ε代表误差项。在有些应用情况下，模型假设截距项β0为零。

（二）回归系数的估计

设(xi,1,xi,2,…,xi,p,yi),i=1,2,…,n,是(X1,X2,…,Xp,Y)的次独立观测值，令

则多元线性模型可表示为矩阵形式Y=Xβ+ε 。其中，β是未知的回归系数向量。最小二乘法通过最小化误差平方和Q(β)=(Y-Xβ)T(Y-Xβ)来求回归系数β的估计值。其他常见的估计方法有最大似然估计和矩估计。可以证明，回归系数β的最小二乘估计为从而可得经验回归方程和残差向量

（三）拟合优度检验

拟合优度是指所建立的回归模型对于数据来说，自变量能够解释因变量的程度。令yi代表yi的估计值，。模型的可决系数为模型的可决系数是一个取值范围在0和1之间的非负统计量。可决系数越大，说明模型的拟合优度越好。在多元回归分析中，调整可决系数剔出了自变量个数对拟合优度的影响，作为综合度量模型对观测值拟合优度的指标，可以有效地防止过拟合。

（四）显著性检验

显著性检验有两种，一种是回归方程的显著性检验；另一种是回归系数的显著性检验。

回归方程的显著性检验，即检验整个回归方程的显著性，或者说评价所有自变量与因变量的线性关系是否密切，一般用F检验法。对于给定的显著性水平α，假设成立时，模型的F统计量服从自由度为（p,n-p-1）的F分布，记为

回归系数的显著性检验，即检验回归模型中各个自变量是否具有显著性，一般用t检验法。给定显著性水平α，对于每一个回归系数βj，模型的t统计量服从自由度为n-p-1的t分布，记为。如果t大于临界值则认为α在水平下回归系数βj显著不为零，即自变量Xi对因变量的线性影响显著。

（五）预测模型结果

当多元线性回归方程经过检验是显著的，且其中每一个系数均显著时，可用此方程作预测。给定自变量将其带入经验回归方程得到估计值和一个置信度为1-α的预测区间，其中

三、建立道路交通事故次数回归分析模型

我国目前在交通安全管理上常采用的指标包括交通事故起数、受伤人数、死亡人数和直接经济损失，即交通事故四项指标。选择交通事故起数这一指标进行回归分析。以某市2005～2012年道路交通事故起数作为因变量，与同期该市的城市GDP、人口数、汽车保有量、城市道路长度、公路客运量、公路货运量共六项影响因素作相关分析，选取相关度高的因素作为自变量建立多元线性回归模型。该市2005～2012年相关数据见表1。

?

（一）相关性分析

回归分析是对具有因果关系的影响因素（自变量）和预测对象（因变量）所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时，建立的回归方程才有意义。进行相关分析，一般要求出相关关系，以相关系数的大小来判断自变量和因变量的相关程度。图1展现了道路交通事故起数与城市GDP、人口数、汽车保有量、城市道路长度、公路客运量、公路货运量之间的散点图。观察可得，事故起数和死亡人数与城市道路长度没有明确的线性关系，与其他各指标呈现明显的负相关关系。

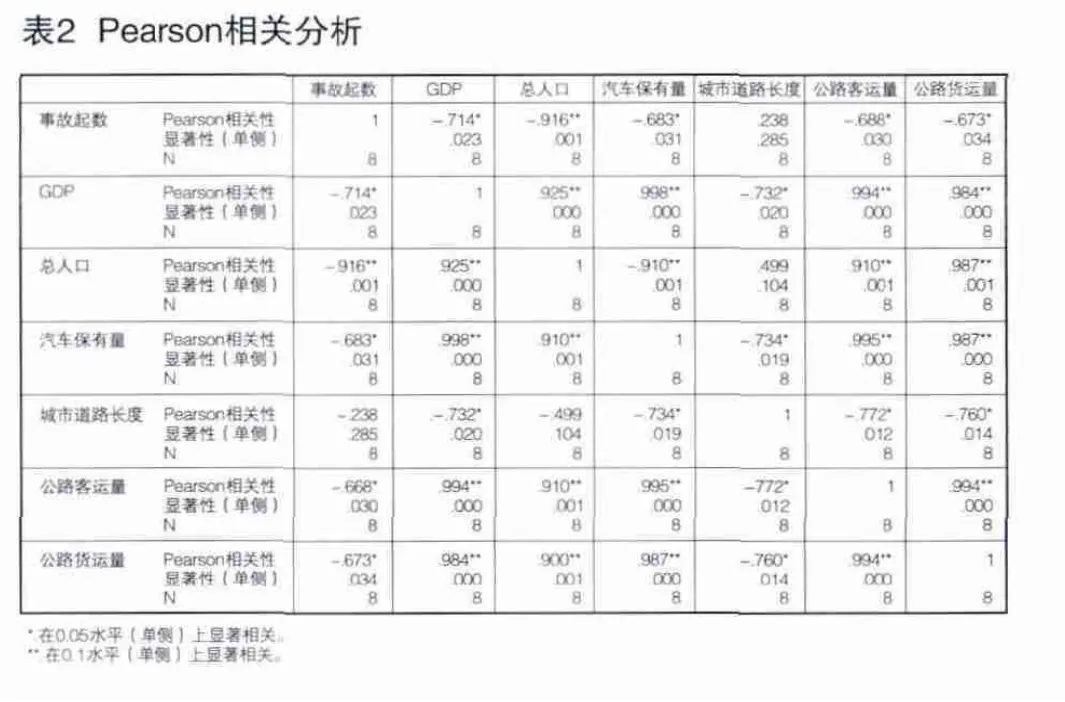
我们进一步对各个变量做Pearson相关分析。对于连续型数值变量，Pearson相关系数是一个介于-1与1之间的统计量，测量了变量之间的相关程度[5]。表2显示了事故起数与各指标之间的Pearson相关系数和对应的单边显著性水平。从表中可以看出，事故起数与人口数之间的相关系数为-0.916，它们在0.05显著性水平下显著负相关；事故起数与GDP、汽车保有量、公路客运量和公路货运量之间的相关系数分别为-0.714、-0.683、-0.688和-0.673，它们在0.05显著性水平下显著负相关。根据散点图和Pearson相关分析，初步将城市道路长度这个影响因素排除。

?

（二）回归方程的建立与求解

一般来讲，如果在一个回归方程中忽略了对因变量有显著影响的自变量，那么所建立的方程必然与实际有较大的偏离，但是如果自变量选的过多，特别是当方程中还有对因变量影响不大的自变量时，就会影响回归方程的拟合优度和预测精度。本文采用逐步回归策略来选择自变量。逐步回归策略按全部自变量对因变量的显著程度大小（贡献程度大小），由大到小地将自变量逐个引入回归方程，而对那些对因变量作用不显著的变量则不被引入回归方程。另外，己被引入回归方程的变量在引入新变量后也可能失去重要性，而需要从回归方程中剔除出去。引入一个变量或者从回归方程中剔除一个变量都称为逐步回归的一步，每一步都要进行F检验，以保证在引入新变量前回归方程中只含有对因变量影响显著的变量，而不显著的变量已被剔除。令y为道路交通事故起数，x1为城市GDP，x2为人口数、x3为汽车保有量，x4为公路客运量、x5为公路货运量。我们采用逐步回归策略，通过SPSS计算求解[5]，得出事故数量的回归方程为，

模型的调整可决系数 R2=0.993，这说明模型的拟合优度较好。由回归方程式可知，GDP与事故数量是负相关的，即随着GDP的增加，事故数呈下降趋势。相反，人口规模与事故数量是正相关的，即随着人口的增加，事故数呈上升趋势。

（三）显著性检验

用F检验法对上述回归方程进行显著性检验，经过计算得出回归方程的F统计量为54.721，在α=0.01水平下是显著的，即认为GDP和人口规模两个影响因素总体对交通事故起数的线性影响是显著的。用t检验法对单个回归系数进行显著性检验，经过计算得出回归系数的t统计量为5.365，在α=0.01水平下是显著的，即认为GDP对交通事故起数的线性影响是显著的；回归系数的 t统计量为-2.496，在α=0.05水平下是显著的，即认为人口规模对交通事故起数的线性影响也是显著的。因此，事故起数与GDP和人口数之间的线性关系显著，建立的上述多元线性回归模型是恰当的。经检验，回归方程及各回归系数都是显著的，给定自变量和置信水平，就可以根据回归方程预测出因变量的估计值和置信区间。

（四）计算并确定预测值

经检验，回归方程及各回归系数都是显著的，那么就可以利用回归模型计算预测值。若该市GDP按8%速度增长，2013年和2014年将分别达到8173.60亿元和8827.49亿元；若该市人口数按0.5%速度增长，2014年将达到472.42万人和474.78万人。根据式(1)中的多元回归分析模型，2013年道路交通事故起数的90%预测上限为2485起，即2013年发生2485起以上道路交通事故的可能性不超过10%；2014年交通事故死亡人数的预测上限为2422起，即2014年发生2422起以上道路交通事故的可能性不超过10%。

四、结语

本文通过建立多元线性回归模型，对某市的道路交通事故数据进行分析和预测。选取道路交通事故次数作为因变量，城市GDP、人口数、汽车保有量、城市道路长度、公路客运量、公路货运量作为自变量，进行多元线性回归分析。分析结果说明，交通事故次数与GDP之间的线性关系是显著的，随着GDP的增加，事故数呈下降趋势。根据结果建立了预测模型，且模型的拟合优度较好，通过了模型的显著性检验。多元线性回归模型是定量分析和预测道路交通事故发展趋势的有效手段之一，可广泛应用于道路交通事故的分析和预测中，科学地对道路交通事故进行预测，从而为科学交通管理提供技术支撑。

[1] 董玉波.道路交通事故多元线性回归模型及检验方法.中国人民公安大学学报(自然科学版), 2013年第2期.

[2] 房曰荣,沈斐敏.道路交通事故发展趋势分析与预测.中国安全生产科学技术,2012年第8卷第2期.

[3] 胡向阳, 姚慧芳.运用回归分析法研究足迹样本.警察技术,2002年03期.

[4] 薛毅,陈立萍. 统计建模与R软件.北京:清华大学出版社, 2007.

[5] 张文,张文彤, 邝春伟. SPSS统计分析基础教程.高等教育出版社,2011.