基于偏最小二乘回归的快速产能评估方法

2014-03-03王佩珊赵立强罗志锋李年银西南石油大学石油工程学院四川成都610500

石油天然气学报 2014年7期

王佩珊，赵立强，罗志锋，李年银（西南石油大学石油工程学院，四川成都 610500）

曾祥宇（中石油吐哈油田分公司开发部，新疆鄯善 838202）

柯建兴（中石油西部钻探公司吐哈钻井公司，新疆鄯善 838202）

库车坳陷西部作为塔里木盆地加快寻找大油气田的主攻地区［1］，是当下热门开发目标之一。区块内多数储层属于异常高压裂缝性储层，地质条件较为复杂，产能有效评估难度较大。目前油气田开发中常用的产能评估手段主要有2种：一是井下测试［2］，但在异常高压储层条件下直接下入井下测试工具风险大且耗时；二是数值模拟［3］，由于裂缝性储层渗流方式复杂，建立和求解数学物理模型难度大。

鉴于上述2种方法的局限性，从统计学角度出发，尝试利用数据挖掘技术直接分析现场数据，以期达到有效评估产能的目标。一种简单可行的方法是利用偏最小二乘法进行多元回归分析，建立产能与影响因素之间的经验模型。

偏最小二乘回归（partial least squares regression，PLSR）是一种多因变量对多自变量的回归建模方法。它集多元线性回归分析、典型相关分析和主成分分析于一体，能够实现对高维数据空间的降维处理［4］，并能有效地解决自变量间多重相关情况下的回归建模问题。同时，PLSR在处理小样本多元数据问题方面也具有明显优势。随着计算机科学技术的发展，PLSR在生物医学、环境工程等许多方面得到了广泛的应用［5～8］，但在石油勘探与开发领域中的应用报道较少［9，10］。

笔者以库车坳陷西部某异常高压裂缝性储层酸压井为例，提出了一种基于偏最小二乘回归和变量投影重要性分析的快速酸压产能评估方法。该方法可用于分析主控因素，预测增产潜力，指导选井选层以及优化施工参数。计算结果表明该方法精度高，实用性强。

1 基础参数相关性分析

库车西部A气藏属于低孔裂缝性砂岩干气气藏，埋深普遍在5000m以上，地层压力因数普遍超过1.5，属超深高压气藏；基质渗透率为0.01～0.1mD，孔隙度为6%～8%，属低孔低渗储层［1］。该区块正处于开发初期，样本资料不多，此处仅收集到了目标区块8口酸压井的地质及生产资料（见表1），正好可以用来检验该方法在处理小样本问题上的有效性。

表1 A气藏部分酸压井基础数据

针对储层具体情况，根据经验选取了10个酸压产能影响因素进行分析与预测，产能基本模型表述如下：

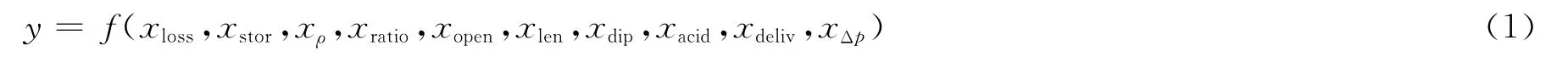
式中：为单井日产气量，m3；xloss为漏失量，m3；xstor为储能系数（hφSg），m；h为储层厚度，m；φ为孔隙度，1；Sg为含气饱和度，%；xρ为裂缝条密度，条/m；xratio为面缝率，%；xopen为张开度，mm；xlen为裂缝视长度，m；xdip为倾角，（°）；xacid为用酸强度，m3/m；xdeliv为排量，m3/min；xΔp为生产压差，MPa。

为了检验各个产能影响因素之间是否存在相关性，引入皮氏积矩相关系数来衡量2个随机变量之间线性相关程度的指标。相关系数计算公式为：

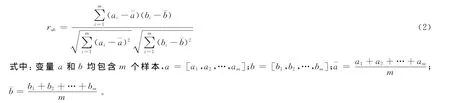
针对例中情况，a和b分别代表不同的影响因子，如xloss和xopen；m取值为样本数8。分别计算两因素之间的相关系数，r如表2所示。各变量间存在一定程度的线性相关性，相关系数绝对值最大为0.86，有8组相关系数在0.500以上，说明影响因素之间存在多重共线性关系。因此，考虑到偏最小二乘回归在消除线性相关影响方面的优势，利用其对这些数据进行分析具有针对性。

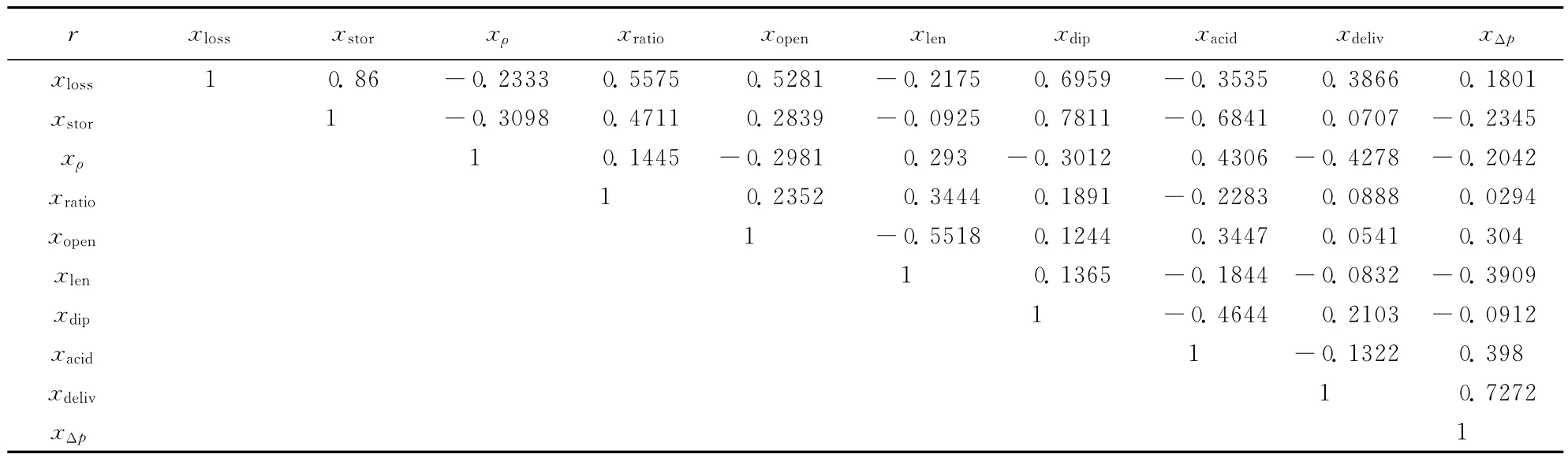
表2 各影响因素相关系数表

2 产能模型建立

分别在产能影响因素集合X＝｛x1，x2，…，xp｝n×p和产能集合Y＝｛y1，y2，…，yq｝n×q中依次提取主成分ti和ui，并要求：①ti和ui尽可能多地携带各自数据表中的变异信息，尽可能好地代表X和Y；②ti和ui的相关程度能够达到最大，ti对ui有最强的解释能力。最终提取出的h个主成分t1，t2，…，th对产能的解释性最强，且克服了各影响因素之间的多重相关性，剔除了噪声信息的干扰。通过实施产能集合Y对t1，t2，…，th的回归（h＜A，A为X的秩），最后表达成产能Y关于原始产能影响因素x1，x2，…，xp的回归方程。

在PLSR中，回归的产能影响因素数目从p降为h，由于h远小于样本数n，解决了小样本问题；且t1，t2，…，th之间相互独立，解决了多重相关性的问题。

利用偏最小二乘方法对表1中前6组数据进行处理，通过Matlab 7.12.0编程实现［11，12］。最终提取2个成分t1、t2，建立了异常高压低孔裂缝性砂岩气藏缝网酸压产能的多元线性回归的经验模型Ⅰ：

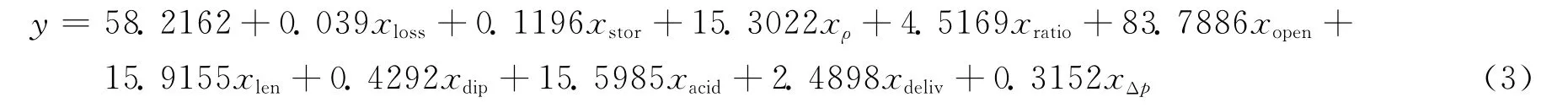
测定系数R2＝0.862697，说明拟合样本数据程度较高。

3 变量投影重要性分析

在产能模型基础上进行变量投影重要性分析，既可以定性分析各因素的影响程度，为后期增产措施提供指导；又可以在变量较多的情况下筛选自变量，简化模型，提高精度，方便现场使用。

变量投影重要性指标Ivip（variable importance in projection）［12］用以测度自变量对因变量的解释能力。其定义式为：

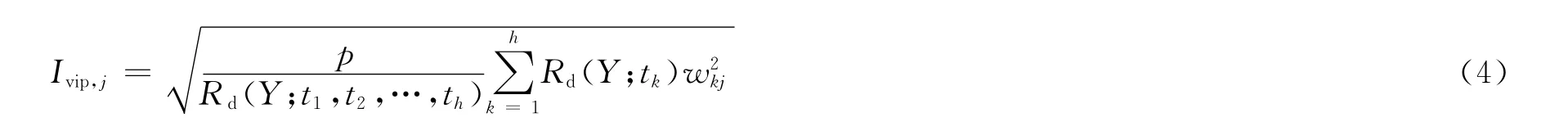
式中：Rd（Y；tk）和Rd（Y；t1，t2，…，th）分别是单个主成分tk对产能Y的解释能力和所有主成分t1，t2，…，th对Y的累计解释能力。对于p个自变量xj，如果它们在解释y时作用都相同，则所有Ivip，j均等于1；Ivip，j越大，则xj在解释y时就越重要。据此，可对各产能影响因素的相对重要程度进行比较，筛选出主控因素。表3为模型Ⅰ中10个影响因素的Ivip值。

由表3可看出，用酸强度对产能的影响最大，其次是漏失量；裂缝参数的Ivip值同样较高，说明天然裂缝性储层中裂缝参数对产能的影响不可忽视。排量、生产压差、储能系数、视长度和面缝率的Ivip值较小，说明它们对产能的解释程度均较小。由此，筛选出目标储层酸压井产能主控因素依次为用酸强度、钻井液漏失量、张开度、裂缝密度和倾角。

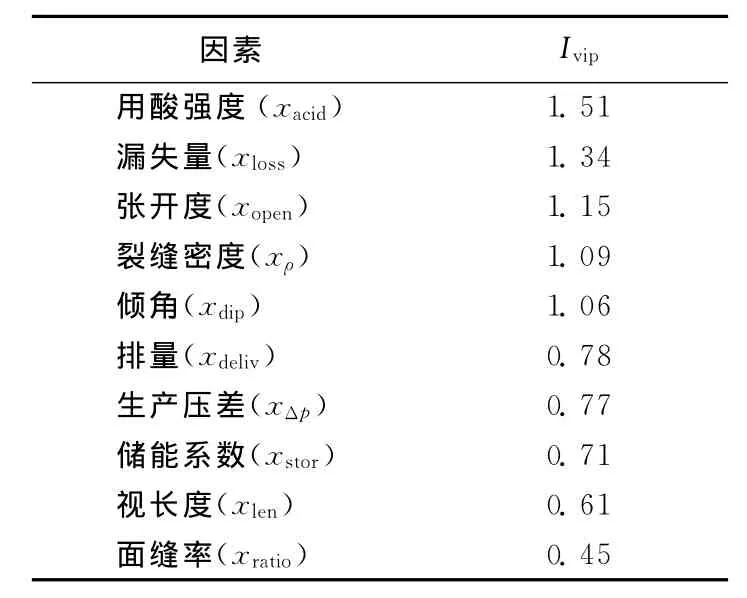
表3 模型Ⅰ中10个影响因素的Ivip值

4 基于主控因素的产能评估模型

由于模型Ⅰ中影响因素太多，计算烦琐，不方便现场快速使用，可考虑仅使用筛选出的主控因素回归得到简化模型。

依照产能建模方法，对于只考虑主控因素的数据组，通过提取2个成分t1、t2，建立了异常高压低孔裂缝性砂岩气藏酸压产能的多元线性回归的经验模型Ⅱ：

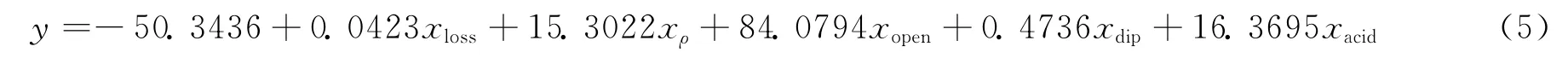
测定系数R2＝0.848796091，说明拟合样本数据程度较高。再次通过变量投影重要性分析，得到了模型Ⅱ中5个影响因素的Ivip值：用酸强度Ivip＝1.18，漏失量Ivip＝1.12；张开度Ivip＝0.96；倾角Ivip＝0.87；裂缝密度Ivip＝0.82。各因素对产能的解释能力差别不大，各自变量解释性均较强，该模型较为合理。