广义S变换在转子碰摩故障诊断中的应用

朱明，李志农，何旭平，邬冠华

（南昌航空大学 无损检测技术教育部重点实验室，江西 南昌330063）

式（4）中：k，p为调节因子，k＞0，p＞0.

对比式（4）和式（1）可知：当p＝k＝1时，广义S变换就退化为标准S变换，即广义S变换继承标准S变换的所有优点，且通过调节因子，增强广义S变换的自适应性，克服了标准S变换存在的不足.

碰摩是旋转机械的一种常见故障，是转子系统发生失稳的一个重要原因［1］.国内外学者对转子碰摩故障诊断也进行了广泛的研究，提出了一些有效的方法 .其中，最典型的是利用小波变换的良好时频局部化特性来分析转子碰摩故障特征.文献［2-3］用小波尺度谱和相位谱对碰摩故障的仿真数据和试验数据进行分析，结果表明小波尺度谱和相位谱在碰摩故障数据的分析方面具有明显的优势.文献［4］利用谐波小波变换对含定子-转子摩擦的裂纹转子滑动轴承系统的振动进行了详细研究.文献［5］用小波时频等高图来诊断质量慢变转子系统的碰摩故障，取得了比较好的效果.然而，在小波变换中，处理非平稳信号时，合适的基函数选择是非常重要的，一旦选择，在分析信号时，基函数就不允许更改，缺乏自适应性.而且小波分解结果只与分析频率有关，与信号本身无关.另外，其基本小波函数还必须满足容许性条件，这些不足或多或少制约了小波变换的应用.因此，需要寻求新的有效的时频分析方法.S变换（S-transform）是继小波变换后新出现的一种时频分析方法，它吸取了短时Fourier变换和小波变换的所有优点，又弥补了各自的不足［6］.S变换既是一种无损变换，又是一种线性变换，时频分辨率与信号本身直接关联.然而，由于S变换中采用的窗函数仍是固定的，缺乏自适应性.为克服此不足，文献［7-9］在标准S变换的尺度因子的基础上，通过引入调节因子，使得窗函数宽度能根据分析信号的频率变化而自适应地调整，这种改进的S变换，称为广义S变换.本文将广义S变换引入到转子碰摩故障诊断中，分析了具有不同严重程度的碰摩故障的振动特性，并进行了实验验证.

1 广义S变换

设x（t）∈L2（R），L2（R）为能量有限函数空间，则信号x（t）的一维S变换定义为

式（1）中：f为频率；τ为时移因子；w（τ，f）为一高斯窗函数；i为虚数单位.相应地，S 变换的逆变换为

由式（1）可知：窗函数的宽度与频率成反比，因而，可以根据信号的频率变化自适应地调节窗函数的宽度，从而得到合适的时频分辨率.因此，标准S变换与小波变换类似，也具有多分辨率特性.然而，标准S变换具有小波变换所不具有的独特性质，如小波变换的分解尺度与信号频率无关，只与分析频率有关，缺乏明显的物理意义.标准S变换与该信号的Fourier变换直接关联，这样，保证了该变换的无损性.这些独特的优势，使得标准S变换比小波变换具有更强的非平稳信号的处理能力.

由式（1）还可知，S变换中的基本小波函数仍是固定的，缺乏自适应性.为此，文献［7-9］通过引入调节参数对标准S变换进行延拓，给出广义S变换（GST），其表达式为

式（4）中：k，p为调节因子，k＞0，p＞0.

对比式（4）和式（1）可知：当p＝k＝1时，广义S变换就退化为标准S变换，即广义S变换继承标准S变换的所有优点，且通过调节因子，增强广义S变换的自适应性，克服了标准S变换存在的不足.

利用傅里叶变换和卷积定理与式（3）推理过程［9-10］，类似可得

式（5）中：X（α＋f）为信号x（t）的傅里叶变换并平移频率α.

式（6）中：j代表时间，j＝0，1，2，…，N-1；n代表频率，n＝0，1，2，…，N-1.

特别地，当n＝0时的离散广义S变换定义为

由式（7）可见：离散形式的广义S变换可以用快速Fourier变换算法和卷积定理来实现，具体计算步骤见文献［10-11］.

2 时频分布的仿真分析

考虑如下仿真信号

图1 信号x（t）的时域波形Fig.1 Time-domain waveform of signal x（t）

由图2，3，4可知：不论是小波变换、标准S变换，还是广义S变换，都有多分辨率分析特性，能明显地反映出信号的两个线性调频部分，具有比较好的时频分辨率.然而，对比这三者的结果发现，它们之间仍有差别.

对比图2与图3可知：广义S变换的时频分辨率明显高于小波变换，尤其是在高频部分 .与广义S变换相比，小波变换对非平稳信号的处理能力是建立在选择合适的小波基的基础上，但到目前为止，如何合理地选择小波基函数是非常困难的，且在理论上也没有给出选择的原则和判断的标准 .另外，小波基函数一经选择，在分析过程中就不能更换，缺乏自适应性.而且，小波分解结果只与分析频率有关，而与信号自身频率没有任何关系.广义S变换不仅吸收了小波变换的所有优点，而且通过调节参数，大大增强了对信号本身分析处理的自适应性，可以灵活调节窗函数的宽度，以达到分析信号时，能获得最佳的时频分辨率.因此，广义S变换比小波变换具有明显的优势.

图2 信号x（t）的广义S变换Fig.2 Generalized S-transformation of signal x（t）

图3 信号x（t）的小波变换Fig.3 Wavelet transform of signal x（t）

图4 信号x（t）的标准S变换 Fig.4 Standard S-transformation of signal x（t）

对比广义S变换和标准S变换发现，两种方法都具有和小波变换类似的多分辨率分析的思想.从图2与图4中可以明显地看出，当频率逐渐增大时，标准S变换的高频部分的分辨率远不及广义S变换.这主要是因为标准S变换中的基本小波函数缺乏自适应性造成的，而广义S变换具有良好的自适应性，获得了比标准变换更高的时频分辨率.因此，广义S变换具有更好的实用性和灵活性.

3 实验验证与分析

为了进一步验证广义S变换的有效性，将利用广义S变换对双盘转子的碰摩试验数据进行分析.图5为转子实验台［3］.图5中：转子由电动机驱动，轴承为滑动轴承，用非接触式电涡流传感器测量垂直与水平方向的振动.

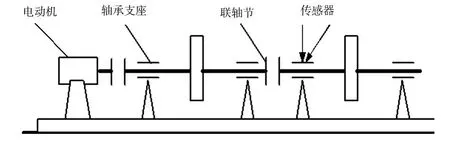
图5 试验台简图Fig.5 Test bench schematic

图6 定子结构示意图Fig.6 Schematic diagram of the stator

为了能更好地模拟出实际碰摩的过程，专门设计了一个有可能产生全周碰摩的定子.转子径向碰摩故障通过图6的装置来模拟，通过置换不同内径的定子，可以模拟不同程度的碰摩故障［3］.在该实验中，转速为3 000 r·min-1，采样频率为1.6 k Hz，采样点数是512.利用传感器获得的两种不同的碰摩程度下的振动信号及其相应的频谱图，分别如图7，8所示.广义S变换的时频分布，如图9所示.为了比较，在此也相应地给出了无碰摩的振动波形、频谱图和广义S变换的时频分布.

由图8（a）可知：无碰摩时只存在1X，不存在其他倍频信息.从图8（b）可知：轻微碰摩故障的频谱图上主要显示了信号的1X和2X谐波分量，而其他谐波分量，包括那些高阶整数倍频谐波分量，相对于1X和2X频谐波分量，在频谱图上都显得很小.由图8（c）可知：严重碰摩产生的冲击在转子振动信号中激发了丰富的频率分量，这些频率分量的幅值也很大.很明显，在频谱图中，并不能反映出信号频率随时间变化的特点.

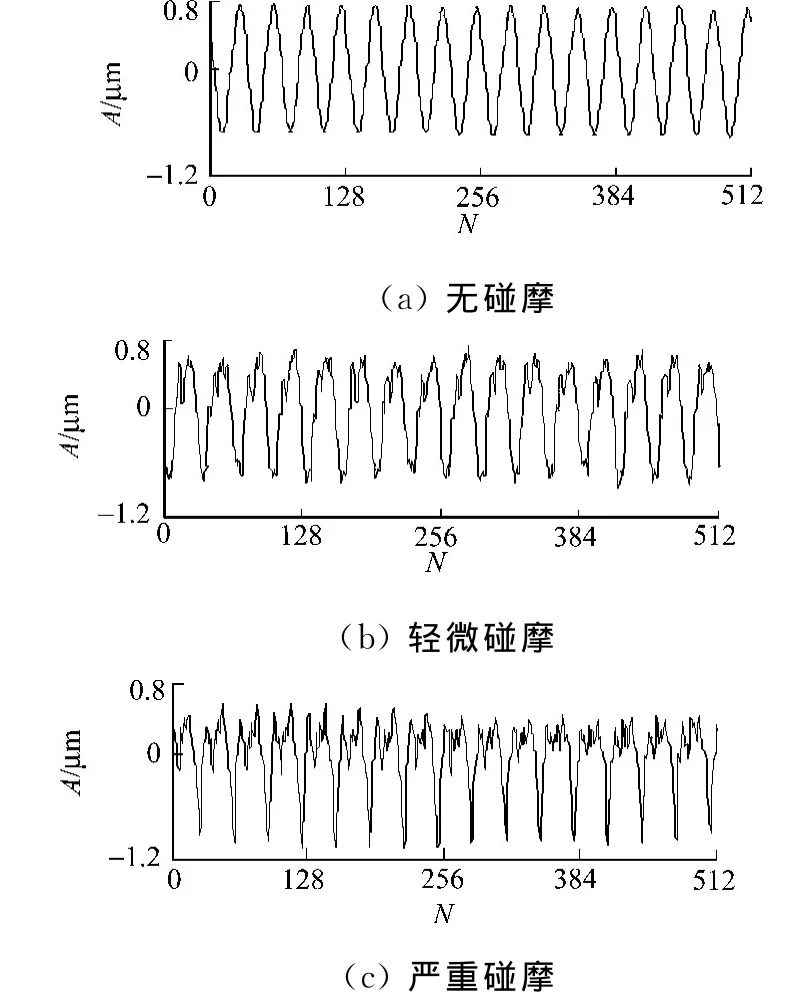
图7 碰摩故障试验振动信号Fig.7 Rub-impact fault test vibration signal

图8 碰摩故障试验振动信号的频谱图Fig.8 Rub-impact fault test vibration signal spectrum

从图9（a）可知：无碰摩时的广义S变换只存在1X，且幅值是连续不变的.由图9（b）可知：信号的1X和2X分量反映明显，基本上比较稳定，而其他高阶分量与1X和2X分量相比较，明显非常微弱，高阶频率分量都是周期性地被激发.对比图9（b）和图9（c）可知：严重碰摩产生的频率成分明显比轻微碰摩更丰富，不仅1X，2X频率成分持续存在，而且3X分量持续存在，且幅值比较稳定，更高阶次的频率成份反映也比轻微碰摩更明显，并且较有规律地间断地出现.

图9 转子碰摩的广义S变换Fig.9 Generalized S-transformation of rotor rub-impact

因此，利用所提出的方法能很好地反映碰摩故障的严重程度，揭示碰摩故障特征.当发生轻微碰摩时，只有一些低阶频率成分持续存在，高阶分量非常微弱.随着碰摩程度的增加，除了低阶频率外，更高的频率成分也会逐渐有规律地间断地出现，并且幅值明显增大.

4 结论

广义S变换是一种新的时频分析方法，该方法通过引入两个调节参数k和p，可以灵活地调节窗函数的宽度，从而能够获得最佳的时频分辨率 .基于广义S变换在处理非平稳信号的独特优势，将广义S变换引入到转子碰摩故障诊断中，提出基于广义S变换的转子碰摩故障诊断方法，分析了具有不同严重程度的转子碰摩故障的振动特性，并进行了仿真和实验验证.

仿真结果表明：广义S变换具有良好的自适应性，在处理非平稳信号时明显优于小波变换和标准S变换.实验结果进一步验证了该方法的有效性，广义S变换能够准确地反映出转子系统无碰摩、轻微碰摩和严重碰摩的振动特征，揭示碰摩故障数据的频率结构，从而有效地提取出了碰摩故障信号的谐波特征，区分转子碰摩故障的不同严重程度.

文中的研究为转子碰摩故障诊断提供了一种有效的方法，同时，对转子系统其他类型故障的分析提供了很好的借鉴作用.

［1］ 卢文秀.旋转机械碰摩的动力学特征与故障诊断［D］.北京：清华大学，2002：1-6.

［2］ 彭志科，何永勇，卢青，等.用小波时频分析方法研究发电机碰摩故障特征［J］.中国电机工程学报，2003，23（5）：75-79.

［3］ 褚福磊，彭志科，冯志鹏，等.机械故障诊断中的现代信号处理方法［M］.北京：科学出版社，2009：31-58.

［4］ WAN Fang-yi，XU Qing-yu，LI Song-tao.Vibration analysis of cracked rotor sliding bearing system with rotor-stator rubbing by harmonic wavelet transform［J］.Journal of Sound and Vibration，2004，271（3／4／5）：507-518.

［5］ 李小彭，姚红良，李鹤，等.质量慢变转子系统的碰摩故障小波分析［J］.中国机械工程，2006，17（14）：1528-1531.

［6］ STOCKWELL R G，MANSINHA L，LOWE R P.Localization of the complex spectrum：The S transform［J］.IEEE Transactions on Signal Processing，1996，44（4）：998-1001.

［7］ PINNEGAR C R，MANSINHA L.The S-transform with windows of arbitrary and varying shape［J］.Geophysics，2003，68（1）：318-385.

［8］ PINNEGAR C R，MANSINHA L.Time-local spectral analysis for non-stationary time series：The S-transform for noisy signals［J］.Fluctuation and Noise Letters，2003，3（3）：357-364.

［9］ 高静怀，陈文超，李幼铭，等.广义S变换与薄互层地震响应分析［J］.地球物理学报，2003，46（4）：512-532.

［10］ 全惠敏.电能质量相关信号的S变换检测算法及应用研究［D］.湖南：湖南大学，2010：15-17.

［11］ 马见青.广义S变换、TT变换及其在地震资料处理中的应用研究［D］.西安：长安大学，2010：18-21.