类锂Zn27+离子的能量和量子数亏损

刘 鑫，王治文

(1河北科技师范学院物理系，河北秦皇岛，066004;2辽宁师范大学物理与电子技术学院)

关于高离化原子的结构和性质的研究在天体物理、激光物理和等离子物理等领域起着重要作用，使得关于高离化原子的结构和性质的研究成为当今国际原子物理的前沿之一［1］。但是目前关于这方面的实验数据少之又少，而且仅有的一些实验数据的精度也难尽人意。在很多情况下还必须依靠准确可靠的理论预言。

近年来，全实加关联(FCPC)方法［2］已被成功地拓展到核电荷较高的体系［3～7］，并与单通道量子亏损(QDT)理论相结合，实现了对这些离子高激发态能量的可靠预言和全能域的理论研究，都取得了令人满意的结果。本研究旨在用FCPC方法研究具有更高核电荷的Z=30的类锂离子1s2nl(l=s，p;2≤n≤9)态的电离势、激发能以及跃迁能。并且得到该Rydberg系列的量子数亏损，实现了对该离子高激发态(n≥10)能量的可靠预言。

1 理论方法

FCPC方法的详细描述可参考文献［2］。它采用平方可积的Slater型基函数系，对于1s2nl组态的三电子体系采用如下形式的有别于传统CI的变分波函数:

其中，A是反对称化算符，等号右边第1项是预先确定好的1s2－原子实波函数与单电子Slater轨道线性组合的乘积，描述原子实中的电子关联和价电子效应;第2项类似于传统的CI展开，描述三电子体系中原子实的弛豫以及其他可能的电子关联效应。Φ1s1s和Φn(i)，l(i)的具体表达式参见文献［2］。(1)式中的线性参数通过求解体系的久期方程确定，非线性参数则在寻求体系能量极值的过程中加以优化。在此过程中得到体系非相对论能量E0，同时体系的FCPC波函数得以确定。

相对论效应和质量极化效应用一级微扰论计算:

其中，H′表示微扰算符，包括质量极化效应以及相对论效应:电子动能的相对论修正、Darwin项、电子接触项、轨道－轨道相互作用。这些算符的表达式可参见文献［2］。ΔE1是来自单粒子微扰算符(包括电子动能修正和Darwin项)的一阶能量修正，ΔE2是来自双粒子微扰算符(包括电子接触项、轨道－轨道相互作用项)的贡献。于是三电子体系的总能量为

为了得到更为精确的结果还计及QED效应。在计算体系的电离势(体系总能量与原子实总能量之差)时，可以认为原子实的QED效应相抵消，于是仅需考虑价电子的QED修正。为此，引入有效核电核，将文献［7］中关于类氢原子的QED效应的表达式用于本计算。该修正包含2个部分:对组态能量重心的修正和对精细结构劈裂的修正，具体形式可参见文献［7］。

库仑势的单电子Dirac方程的能量本征值(不包括静质能)为［7］:

其中，k=j+1/2(j是氢原子的总角动量)。仅考虑α2Z4阶的贡献，EDirac约化为:

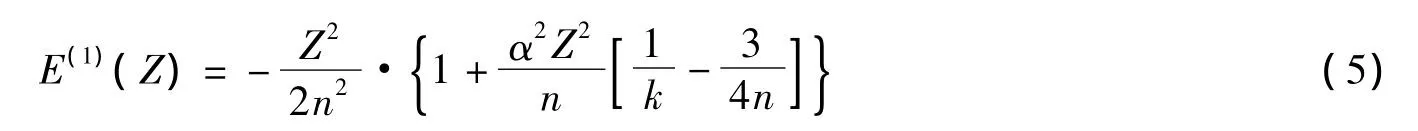
由于在(2)式的计算中，得到的体系nl电子的能量正是仅考虑到α2Z4阶的相对论修正的结果，所以，利用如下的表达式定义有效核电荷:

利用确定的Zeff，可以估算nl电子的ΔEQDT，也可以给出能量的高阶相对论修正:

Zn27+离子1s2nl态的电离势由三电子体系能量与原子实能量之差给出:

上式中等号右边最后一项是QED效应对组态能量重心的修正。

由此可以得到体系的激发能:

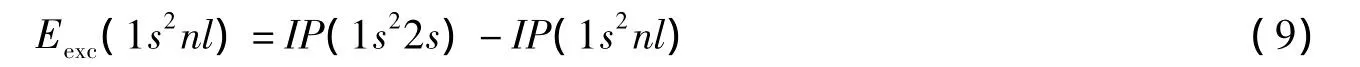
类锂体系1s2nl各态之间的跃迁能由两态电离能之差确定。

根据QDT［8］，能量为En的原子体系的量子数亏损μn与En有如下关系:

其中，n是主量子数，能量En由FCPC方法计算得到。对于高激发态，量子数亏损是随能量缓慢变化的函数，并在体系能量趋于电离阈时趋近于常数，因此可将其按能量做如下展开:

其中，μ0是电离阈处的量子亏损，h1和h2为待定系数。它们由FCPC方法得到的体系低激发态(n≤9)能量和(10)式得到的μn通过迭代方法确定。将确定好的量子亏损作为输入，根据(10)式就可以预言任意高激发态能量。

2 结果与讨论

对于1s2－原子实波函数，用7个分波共222项基函数展开。三电子波函数中价电子效应部分分别选取了9项和10项，描述其他可能的关联效应和原子实弛豫效应的CI波函数分别选取了13个分波和17个分波，项数从688到1060不等。在求能量过程中，数值收敛相当好，从而保证了计算中所用的波函数足够准确。

由(8)式得到Zn27+离子的1s2nl(l=s，p;2≤n≤9)组态的电离势与已有的实验数据［9］已并列于表1中。从表1中可以看到，对于Zn27+离子的2个Rydberg系列，随着主量子数n增大，电离势减小。即越靠近于电离阈，电离势越小。本研究的计算结果与现有的实验数据符合得很好。注意到对于1s2nl(l=s，p;3≤n≤9)组态的电离势没有相关的实验数据，希望这些可靠的理论结果能为试验工作和相关领域的研究提供有益的参考。1s2np态的激发能(相应于能级重心的能量)如表2所示。迄今只有1s22p的实验数据，可以看到二者符合得很好。Zn27+离子1s22s－1s2np(2≤n≤9)的跃迁能的计算结果和已有的实验数据结果如表3所示。希望这些理论结果能对试验工作者进行更加精确的测量提供帮助。

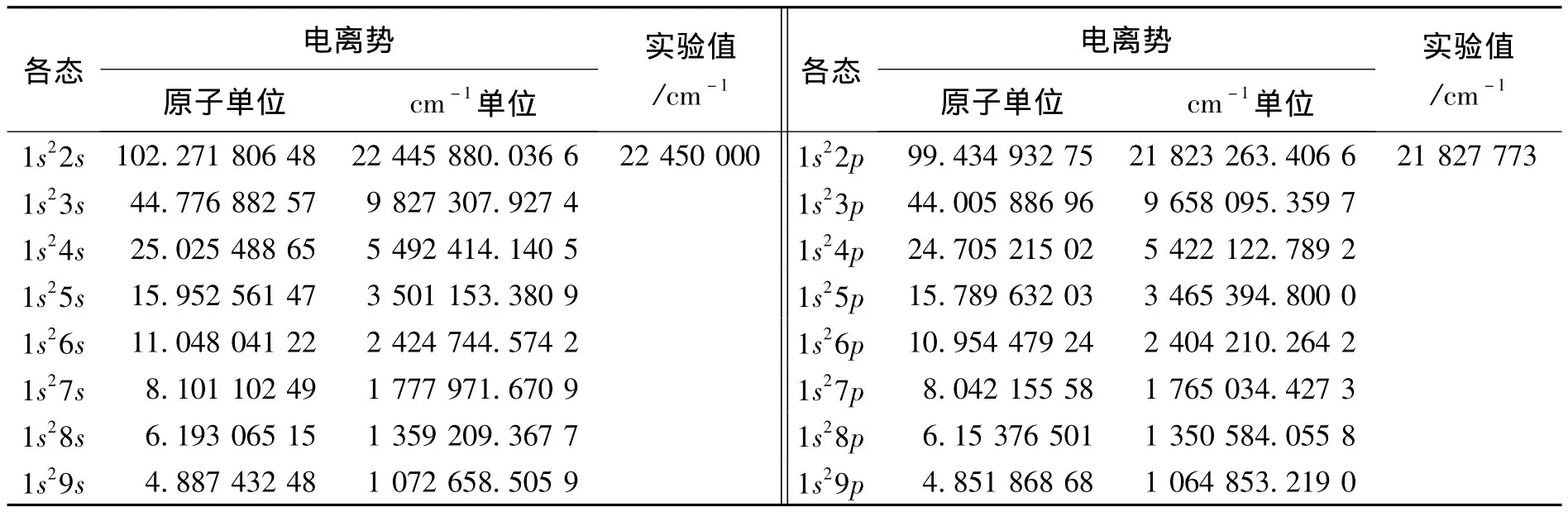
表1 Zn27+离子1s2nl(l=s，p)态的电离势

表2 Zn27+离子1s2np态的激发能

表3 Zn27+离子各态间的跃迁能

量子数亏损按能量展开(如(11)式所示)的待定系数如表4所示。通过迭代方法求解(10)和(11)式，得到Zn27+离子1s2np(6≤n≤9)态的能量，其结果与用FCPC方法得到的从头算结果如表5所示。从中可以看出二者的结果非常接近，相对误差一般不超过万分之一。这表明，本研究确定的Zn27+离子的这个Rydberg系列的量子数亏损是准确可靠的，据此可以准确可靠地预言这些Rydberg系列的任一高激发态(n＞9)的能量。

表4 1s2np态量子数亏损的能量展开系数

表5 FCPC方法与半经验方法得到的1s2np(n≥6)能量结果

3 结 论

利用FCPC方法计算了类Zn27+离子1s2np组态(n≤9)的电离势、激发能和跃迁能。在得到的这些能量的基础上，根据单通道量子亏损理论确定了该离子的1s2np Rydberg序列的非相对论量子数亏损。用这些量子数亏损作为输入，利用半经验方法相当好地重复了上述关于较低激发态能量的FCPC计算结果，从而确保了用本研究得到的Rydberg序列的量子数亏损预言该离子在第一电离阈以下的任意激发态能量的准确性和可靠性。

［1］ Fang T，Canizares C R.Probing Cosmology with the X-Ray Forest［J］.J Astrophys，2000，15(2):532-539.

［2］ Gillaspy J D.Highly charged ions［J］.J Phys B，2001，34:93-130.

［3］ 李金英，王治文.原子结构中求解Hartree-Fock方程的几种方法及其比较［J］.大学物理，2011，30(12):21-25.

［4］ 胡木宏，王楠，王治文，等.Co24+1s2nd(3≤n≤9)态的激发能和精细结构［J］.辽宁师范大学学报:自然科学版，2010，33(4):436-438.

［5］ 蔡娟，于伟威，张楠.原子核体积效应对类锂离子体系激发态能级结构的影响［J］.辽宁师范大学学报:自然科学版，2014，37(3):342-345.

［6］ 刘鑫.类锂钒离子1s2nd－1s2nf的振子强度［J］.河北科技师范学院学报，2010，24(1):5-7.

［7］ Wang Z W，Liu Y，Hu M H，et al.Transition energy and dipole oscillator strength for 1s22p－1s2nd of Cr21+ion［J］.Chin Phys，2008，17(8):2 909-2 913.

［8］ Bethe H A，Salpeter E E.Quantum Mechanics of One-and Two-electron Atoms［M］.Berlin Heidelberg New York:Springer，1977.

［9］ Sugar J，Corliss C.Atomic energy levels of the ion period elements:Potassium through Nickel［J］.Phys Chem Ref Data，1985，14(2):357-371.

(责任编辑:石瑞珍)