基于电阻法的钢桥疲劳裂纹检测方法研究
2014-03-01袁周致远吉伯海傅中秋
袁周致远,吉伯海,傅中秋,刘 荣,程 苗
(河海大学 土木与交通学院,江苏 南京210098)
近年来,交通基础建设得到迅猛发展,各地兴建了大量的大跨度钢桥,但钢材的自身特点在车辆荷载的反复作用下容易产生疲劳损伤。常用的探伤的方法主要有超声波探伤、磁粉探伤及射线探伤。超声波探伤对粗糙、形状不规则、小、薄或非均质材料难以检测。磁粉探伤只能针对表面或近表面的裂纹。射线探伤由于其器材费用高、对人体有伤害、且检测速度慢、携带不方便,不易发现小裂纹而不适用于桥梁钢面板的检测。
目前,电阻法[1]探伤已经初步在许多领域应用起来,但更多地仅限于金属构件的损伤检测[2-4]、评定[5]及预测金属材料疲劳寿命[6-7],对于钢桥面板疲劳裂纹检测尚未研究和应用。笔者提出了基于电阻变化规律[8]来检测钢桥面板疲劳裂纹的方法,在理论与有限元分析基础上,对测量影响因素及测点布置[9-11]方式进行的研究分析,通过U肋部位疲劳裂纹试验验证,并计算出检测部位有效损伤率及断面损伤面积,给出3种适合实际裂纹检测的方法。
1 电阻法检测原理
假设钢板的标准电阻值为R0,实测电阻值为R1,则断面损伤率D按式(1)计算:
(1)
对于电阻法检测裂纹而言,其断面损伤率D按式(2)计算:
(2)
式中:A0为断面面积;A1为损伤面积。
根据断面损伤面积A1和测点有效分布宽度b可推算裂纹的等效深度[12]h:
(3)
断面损伤面积是针对每个测点而言的,如图1。在水平钢板上施加电流时,电流有一定的有效分布宽度b,其值的大小与两电极之间的距离L有关,L越小,b值就越小。因此在合理的测点布置情况下,测点之间的距离B就可以作为有效分布宽度b的值。
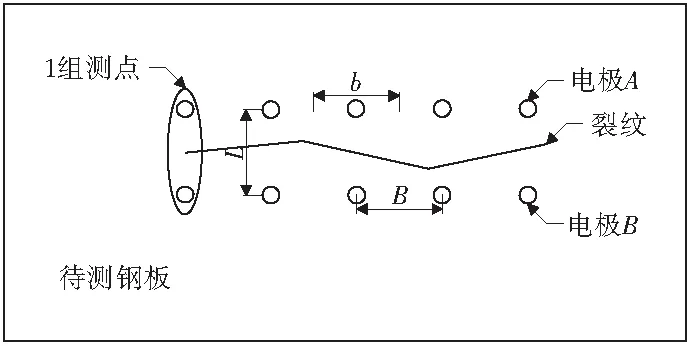
图1 有效分布宽度示意Fig.1 Effective distribution width
2 电阻法检测影响因素分析
2.1 板 宽
板宽影响着电阻计算的边界条件。图2(a)表明:在同一电极间距下,板宽达到一定时,电阻值逐渐趋于平稳,该平稳点可以当作测点的有效分布宽度。不同电极间距对比看出电极间距越小,其趋于平稳的板宽越小。减小测点间距,能够沿裂纹方向布置更多的测点,提高检测的准确性。
2.2 电极间距
保持板宽不变,建立电极间距与测点电阻值之间关系,如图2(b)。板宽越小,电阻值对电极间距的变化敏感性大;板宽越大,电阻值的变化幅度就越小。对于钢桥面板来说,其板宽相对于电极间距,可以当作无穷大,即每组测点的边界条件近乎是一致的。因此,在对隐蔽裂纹进行初步探查时,增大电极间距对于探测裂纹的灵敏度无多大影响。


图2 电阻变化规律Fig.2 Variation of electrical resistance
2.3 裂纹附近测点有限元分析结果
有限元实体模型的尺寸为600 mm × 600 mm × 14 mm的平钢板,中间设一短裂缝,如图3。沿x轴方向每隔50 mm分别布置11个测点。得到11组电阻值,绘制成折线图,见图4。
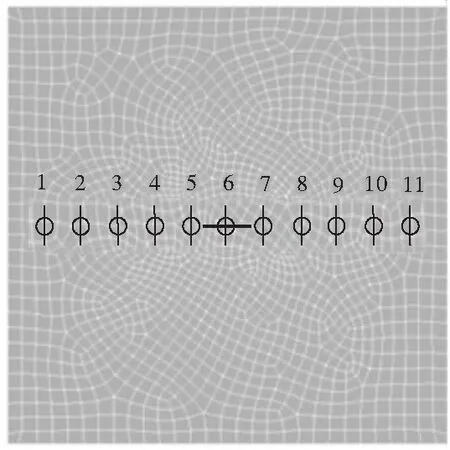
图3 带裂纹平板有限元模型和测点布置情况Fig.3 Finite element model of deck with the crack and layout of measurement points
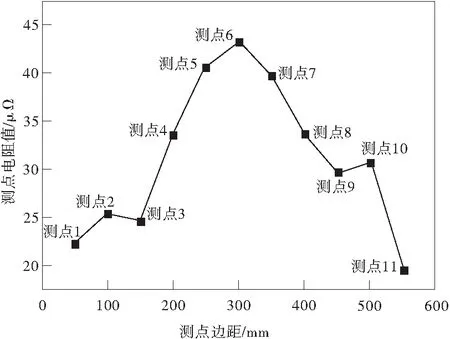
图4 裂纹附近测点阻值变化规律Fig.4 Changing law of electrical resistance near the crack
从图4看出,位于裂纹附近的电阻值比其它测点电阻值大,曲线呈现明显的单峰。由此可以判断曲线峰值附近对应的部位存在缺陷或裂纹。从图4中曲线趋势来看,裂纹存在于测点4~测点8之间。位于裂纹远处的测点,如测点1~测点3,测点9~测点11的电阻值大小受单元划分及邻近测点电流干扰存在正常波动。
笔者针对电极间距分别为100,200 mm做了电阻值计算分析对比,如图5。电极间距越大,曲线峰值越不明显,裂纹判断的准确度也会降低;但曲线峰值对应的测点边距近似一致。因此,大电极间距只能够用于初步扫查,确定裂纹初步位置,小电极间距用于准确定位和确定裂纹起始点。

图5 不同电极间距下裂纹附近测点阻值变化规律对比Fig.5 Comparison of changing rule of electrical resistance near the crack with different electrode spacings
3 裂纹分布结果判断
改变测点布置方式,以裂纹中心为圆心,电极间距为直径,依次布置11个测点,如图6。

图6 环形电极有限元模型及测点布置Fig.6 Finite element model of annular electrode and layout of measurment points
绘制似“雷达图”,如图7。其中测点6的电阻值最大,测点1电阻值最小。从实际测点布置与裂纹开裂方向来看,测点6对应的方向近似为裂纹方向,通过寻找测点最大值可以判断裂纹方向。增加测点数量,能够提高准确度。

图7 环形电极测点电阻值变化规律Fig.7 Changing law of annular electrode resistance at measurement points
4 电阻法裂纹检测方法应用
4.1 测点设计
测点设计主要包括两方面的内容:①开裂部位检测的测点设计;②裂纹走向的测点设计。前者的作用是检测是否存在裂纹,后者的作用是判断裂纹的走向。
1)表面可见裂纹。由于其已经被发现,故可以直接在裂纹附近布置测点。对于1组探头测量而言,可采用逐点测量法(图8),即沿着裂纹方向布置的测点逐个测量。对于多组探头,可采用跳点测量法(图9),即先测量相隔1或2个测点上的电阻值,然后再回过来测量剩余点处的电阻值。

图8 逐点测量法示意Fig.8 Point by point method

图9 跳点测量法示意Fig.9 Jump point method
2)隐蔽裂纹。首先增大探头间距,提高检测范围,待发现电阻变化后,采用逐步逼近法,减小探头之间距离,提高检测精度(图10)。检测到裂纹后,采用环形测点法(图11)进行裂纹走向判定。测点最大阻值所对应的方向可近似作为裂纹开裂方向。沿着预判方向继续测查,直到每个方向测点电阻值近似相等,将预判方向依次连接,即可当作裂纹延伸走向。
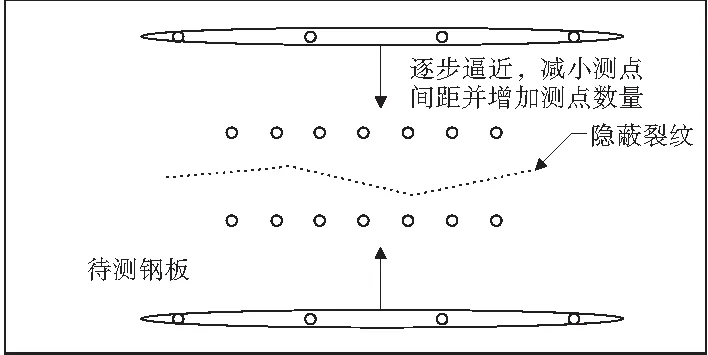
图10 逐步逼近法测量示意Fig.10 Stepwise approximation method
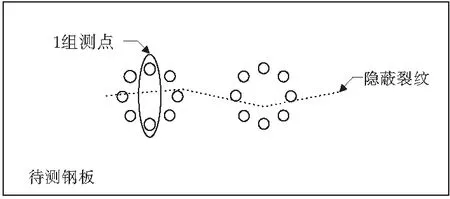
图11 裂纹走向测点布置Fig.11 Crack trend and layout of measurement points
4.2 试验试件及装置
本验证试验采用的双臂电桥型号为QJ84A。试件材料为Q345钢材,模拟钢桥面板与U肋连接部位。该试件已经过疲劳试验,在面板和U肋连接处产生沿U肋纵向的裂缝,如图12。
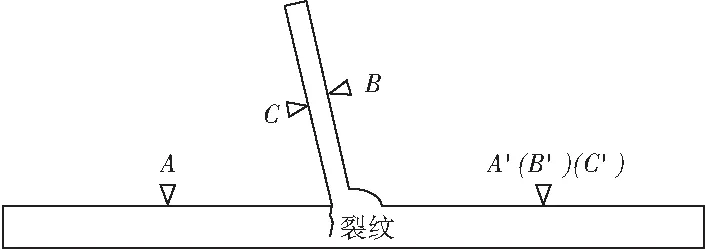
图12 试件断面Fig.12 Fracture of specimen
4.3 检测结果分析
双臂电桥装置分别在U肋两侧(A、A′)、U肋外面(B、B′)、U肋内面(C、C′)布置。实测钢板沿程电阻值数据如表1,沿程电阻变化如图13。

表1 钢板沿程实测电阻值

图13 钢板电阻沿程变化Fig.13 Electrical resistance of specimen
除去该异常点,可以看到其他测点电阻值的变化规律,如图14。U肋两侧电阻值随着测点边距增大,曲线逐渐向上延伸。在测点边距25.5 cm处电阻值达到最大。这说明沿着U肋纵向,裂纹深度增大,截面损伤严重。

图14 去除异常点后实测电阻变化规律Fig.14 Electrical resistance of specimen removing abnormal point
在U肋外面测点和U肋内面测点的电阻值,存在小幅波动,曲线峰值不明显。考虑焊缝尺寸不均匀及测量误差,相对于U肋两侧,可以认为U肋和顶板连接处不存在疲劳裂纹。这也符合实际钢板疲劳裂纹开裂变化情况。
由式(1)、式(3)对U肋两侧分别计算截面损伤率D和裂纹等效深度h,结果如表2。

表2 截面损伤率和裂纹等效深度计算结果
试件实际厚度为1.4 cm。试件切割后通过断面观察疲劳裂纹,在测点边距2.3 cm处几乎不存在疲劳裂纹,把该处的阻值作为标准阻值。在测点边距为25.5 cm处钢板疲劳裂纹计算深度为1.32 cm,符合实际近乎裂透的情况,并有一定的铁锈。因此在该测点的U肋实测电阻值相对于其他测点阻值异常,并且很大。
5 结 论
1)电极间距越小则检测精度越高。在实际钢桥面板疲劳裂纹检测中,测点的边界条件可以认为近乎一致,电极间距的大小对实测值的变化影响较小。因此大电极间距适合裂纹位置的初步判断,小电极间距适合裂纹的精确定位。
2)对裂纹附近测点进行设计,建立裂纹分布结果的判断方法并提出逐点测量法、跳点测量法、环形测点法3种测量方法,用于检测裂纹开裂部位及判断裂纹延伸方向。
3)对存在疲劳裂纹的试件进行测量,得到测点沿程变化情况。计算所得的断面损伤率和裂纹等效深度符合钢板实际裂纹深度情况,验证电阻法检测钢桥疲劳裂纹方法具有较好的精度。
[1] 郑庆华,童悦.双臂电桥测低电阻[J].物理与工程,2009,19(1):36-38.
Zheng Qinghua,Tong Yue.Low resistance measurement by double bridge [J].Physic and Engineering,2009,19(1): 36-38.
[2] 唐文强.双臂电桥测量低电阻中接线问题[J].仪器仪表用户,2005,12(5):105-106.
Tang Wenqiang.Wiring question in double armed electric bridge measure low resistance [J].Instrumentation Customer, 2005,12(5):105-106.
[3] 孙斌祥,郭乙木.考虑电阻率变化的电阻法预测金属材料剩余寿命[J].工程设计,2001(2):81-84.
Sun Binxiang,Guo Yimu.Estimation of remaining life of metallic materials by electrical resistance method considering variable resistivity [J].Engineering Design, 2001(2): 81-84.
[4] 黄丹,许平聪,郭乙木.金属疲劳剩余寿命预测模型的一种探索[J].实验力学,2003,18(1):113-117.
Huang Dan,Xu Pingcong,Guo Yimu.A research on the estimation of remaining service life for metals in fatigue [J].Journal of Experimental Mechanics, 2003,18(1): 113-117.
[5] 袁立方.基于电阻法的30Cr1Mo1V汽轮机转子蠕变寿命研究[D].长沙:长沙理工大学,2007.
Yuan Lifang.Study of Creep Life of Steam Turbine Rotor Steel 30Cr1Mo1V Based on Electrical Resistance Method [D].Changsha: Changsha University of Science & Technology, 2007.
[6] 马宝钿,杜百平,朱维斗,等.电阻法检测疲劳损伤及预测修复效果探讨[J].理化检验:物理分册,2002,38(11):493-495.
Ma Baotian, Du Baiping, Zhu Weidou, et al.Fatigue damage evaluation and repairing effect prediction by electrical resistance measurements [J].Physical Testing and Chemical Analysis Part A: Physical Testing, 2002, 38(11): 493-495.
[7] 黄丹,章青,郭乙木.电阻法检测金属构件损伤及预测疲劳寿命[J].无损检测,2008,30(4):213-215.
Huang Dan,Zhang Qing,Guo Yimu.Damage measurement and fatigue life prediction for metallic components by electrical resistance method[J].Nondestructive Testing, 2008, 30(4): 213-215.
[8] 马宝钿,杜百平,朱维斗,等.从电阻变异规律分析疲劳损伤件中温热等静压效果[J].测试技术学报,2002,16(增刊1):337-340.
Ma Baotian,Du Baiping,Zhu Weidou,et al.HIP effect on fatigue damaged specimens by electric resistance variation [J].Journal of Test and Measurement Technology, 2002, 16(S1): 337-340.
[9] Todoroki A,Omagari K,Shimamura Y,et al.Matrix crack detection of CFRP using electrical resistance change with integrated surface probes[J].Composites Science and Technology,2006,66:1539-1545.
[10] Todoroki A,Tanaka M,Shimamura Y.Electrical resistance change method for monitoring delaminations of CFRP laminates [J].Composites Science and Technology, 2005, 65: 37-46.
[11] Jie Wen,Zhen Haixia,Choy F.Damage detection of carbon fiber reinforced polymer composites via electrical resistance measurement [J].Composites:Part B, 2011, 42: 77-86.
[12] 王苗苗,曾燕屏,王习术,等.航空用超高强度钢疲劳裂纹表面长度与内部长度之间的关系[J].航空材料学报,2009,29(3):102-106.
Wang Miaomiao, Zeng Yanping, Wang Xishu, et al.Relationship between surface length and inside length of fatigue crack in ultra-high strength steel [J].Journal of Aeronautical Materials, 2009, 29(3):102-106.
