基于矩阵对数累积量的极化合成孔径雷达数据去噪方法

刘坤，马文萍，刘红英，王爽

(西安电子科技大学 智能感知与图像理解教育部重点实验室 智能感知与计算国际联合研究中心，陕西西安710071)

0 引言

近些年，随着成像雷达技术的不断发展，越来越多的对地观测合成孔径雷达(SAR)系统具备了多极化或全极化成像能力。2014年4月和5月欧州太空局(ESA)与日本宇航局(JAXA)接连发射了两颗具备全极化成像能力的新一代雷达卫星Sentinel-1A与ALOS-2/PALSAR-2，以全面提升自身的极化SAR(PolSAR)对地遥感能力。美国、加拿大等遥感强国也在按计划逐步推进各自的PolSAR 技术发展与空、天基PolSAR 平台的更新换代，PolSAR 领域的发展日新月异。与单极化SAR 类似，斑点噪声抑制同样是PolSAR 数据处理的关键。相干斑噪声不仅影响PolSAR 图像的视觉效果，更给大数据背景下Pol-SAR 图像的智能理解、解译带来了困难。

经过近20 多年的不断发展，PolSAR 去噪已经有了许多成熟的方法。如由Lee 滤波发展出来的精致极化Lee 滤波［1］、Sigma 滤波［2］、IDAN 滤波［3］等。其中精致极化Lee 滤波因其可靠稳定且对后续的分割、分类影响正面应用最为广泛。近期随着一些新的图像分析方法和数学工具的发展，又涌现出许多PolSAR 去噪新方法。例如基于双边滤波的方法［4］等。其中在基于图像的去噪算法中非局部方法［5］异军突起并已逐步应用于单、多极化SAR 去噪领域。其中PPB 算法［6］利用贝叶斯定理将非局部方法应用于单极化SAR 当中，去噪效果得到本领域研究者的公认，并且在简单假设相干矩阵仅有主对角线元素的前提下将该方法推广到了PolSAR 去噪当中［7］。而以复Whisart 分布模型的统计分析为基础的Pretest 算法［8］在滤波中更是利用到了相干矩阵的全部元素，作为极化滤波方法更为合理，效果也更加优秀。非局部方法作为一种空域去噪方法，同质区域选取以及相似性计算是关键。其相对于传统“局部”方法能取得更好去噪效果的原因在于该方法是面向图像块的去噪方法，这种基于图像块的计算可以更好地利用图像的结构信息，从而在图像结构和细节信息的保持方面有突出的表现。对于PolSAR 数据来说，地物特性通常也体现为图像上的结构和细节信息，因此该方法也适合于处理PolSAR 数据。

Anfinsen 等在复数域的梅林变换的基础上对PolSAR 数据进行了统计分析，并在复矩阵对数累积量的基础上提出了PolSAR 数据Goodness-of-Fit(GoF)检测方法［9］。GoF 检测可以通过假设检验来分析PolSAR 数据的两个样本集是否符合相同参数的Wishart 分布。但是该方法要求用来测试的样本集包含足够大的样本数量，并且理论上应该是同一散射点的多次独立观测。Anfinsen 等［9］在模拟数据上验证了该理论，并在真实数据上采用手工选取同质图像块进行了简单的验证，上述工作表明该统计方法适用于分析PolSAR 数据，但是还未将其真正应用于PolSAR 数据去噪或地物分类中。

对于PolSAR 数据，多视处理是常用的去噪策略。多视处理的一个重要假设就是同一数据点的各子视图像可视为同一散射点的多次不同观测。受此启发本文结合非局部方法和Anfinsen 的理论［9］提出了一种基于复矩阵对数累积量的PolSAR 数据非局部去噪方法。该方法利用非局部策略选择同质区域，然后根据同质区域数据点的子视数据集，基于复矩阵的对数累积量以GoF 方法计算同质区域的相似度，并以此为依据计算滤波权值。在非局部思想下进行的同质区域选取保留了非局部方法对图像结构保持较好的优点，而在子视数据集基础上计算相似度则结合了PolSAR 数据的散射特性。该方法将PolSAR 数据散射特性和图像结构特性相结合，将基于复矩阵对数累积量的GoF 检测方法成功应用到了PolSAR 数据处理中。该方法的优点在于同质区域选取和滤波系数的计算均是针对相干矩阵进行的，相对于仅使用主对角线上的元素或SPAN 图像，其对极化数据的处理更具合理性。

1 基于PolSAR 复相干矩阵对数累积量的相似度计算

1.1 基于PolSAR 数据的矩阵对数累积量的计算

雷达目标的变极化效应可以用一个复二维矩阵的形式来表示，称为极化散射矩阵或Sinclair 矩阵，用矩阵S 来表示［10］:

式中:h 和v 分别表示水平和垂直极化。散射矩阵也可用其矢量形式表示为散射矢量:

满足完全发展的相干斑的条件时，散射矢量服从复高斯分布，其多视图像的协方差矩阵C 为

式中:L 为视数;上标H 表示复共轭转秩。

设d×d 复矩阵C 的概率密度函数为fC(C).

函数g(C)的梅林变换定义为

式中:Ω+表示埃尔米特正定矩阵锥。fC(C)的梅林变换定义为

当φC(s)存在时:

第v 阶对数矩阵(MLM)为

第v 阶矩阵对数累积量(MLC)为

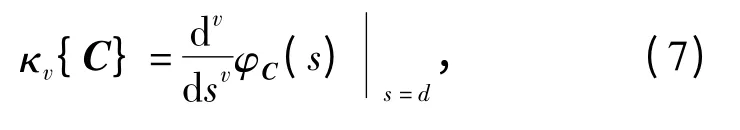
式中:

MLC 可由MLM 按照下式计算得出:

PolSAR 数据中，一个数据点的n 个子视数据可视为n 个独立同分布的复矩阵Ci，该数据点的MLM以及MLC 可以如下计算得出。

第v 阶MLM:

第1 ～vp阶MLM 构成vp阶MLM 向量:

MLC:

将〈μv{C}〉简记为〈μv〉，按照(9)式可得第v 阶MLC 为

第1 ～vp阶MLC 构成vp阶MLC 向量:

1.2 基于GoF 检测的统计检验值计算

Anfinsen 等基于GoF 检测经推导得到了检测两个样本集是否符合同一分布的统计检验值Qp的计算方式［9］:

式中:〈κ〉1与〈κ〉2分别为来自两组样本的MLC;K为向量

的协方差矩阵，

这里给出vp=8 时K4的表达式:记k=〈κ〉2，则

式中:

2 结合非局部均值的去噪算法

2.1 基于非局部均值的同质区域选取

非局部均值方法通过两个图像块之间所有对应数据点的相似程度总和来衡量图像块中心像素的相似程度。图像中每一个像素点的滤波结果由搜索窗内同质区域中所有像素点按照与待滤波点的相似程度加权得到。本文采用Pretest 方法［3］中的阈值方法来选取同质区域。为了保证滤波结果能够保持图像的结构特征，同质区域选取是在空域多视平均过后的图像上进行的。任意两个图像块之间可计算统计检测值:

式中:d 为相干矩阵的阶数;w 为一个图像块中的点数;Xi与Yi分别为两个图像块对应位置处的相干矩阵。如图1所示。

图1 非局部方法选取同质区域示意图Fig.1 Homogeneous region selected using non-local method

阈值可以通过下式进行估计:

对搜索窗内所有非待滤波点计算ln H，当

时将该点记入待滤波点的同质区域参与滤波。

2.2 计算同质点与待滤波点的相似度并加权去噪

非局部方法中两点之间的相似度也是通过两点所在图像块之间的相似度进行计算的。而对于未经过多视处理的PolSAR 数据而言，两个点对应的两组子视数据集同样可以很好地反应出相似程度。

包含n 个子视数据的数据点的MLM 可利用其各子视C 矩阵Ci(i=1，…，n)按照(10)式的计算方法计算得出。这样其MLC 可按照(12)式的计算方法计算得出。数据点1 和2 的相似程度可以由Qp反映出来，Qp按照(14)式计算得出。

滤波权值为

式中:α ＞0 为常数，用于调整滤波效果。

本文算法步骤如下:

步骤1 对全图数据求所需要的行列式等后续计算需要的变量。

1)计算空域多视平均并选择K 矩阵的阶数vp.本文中选用vp=4.

2)计算子视数据以及多视数据的C 矩阵的行列式。

3)由子视数据行列式按照(10)式计算2vp阶MLM 向量，按照(12)式和(13)式计算2vp阶MLC向量并按照(16)式计算vp阶K 矩阵。本文中使用(17)式计算4 阶K 矩阵。

步骤2 对一个待滤波点进行滤波。

1)对待滤波点选择同质区域。按照(23)式选取合理的阈值ln Ht. 由空域多视平均结果在搜索窗内按照(22)式计算搜索窗内所有点与待滤波点的统计检验值ln H，并按照(24)式选择该待滤波点的同质区域。

2)计算同质点的滤波权值。由同质区域中所有点的MLC 向量以及待滤波点处的K 矩阵按照(14)式计算Qp，并按照(25)式计算滤波权值ω.

3)对待滤波点加权滤波。该待滤波点C 矩阵滤波结果为

式中:m 为同质区域中的数据点数。

步骤3 循环下一待滤波点，按照步骤2 进行滤波。

本算法的运算复杂性主要由Pretest 方法选取同质区域的运算复杂性决定，在文献［3］中有该方法的快速算法，按照该快速算法如将(22)式中的计算视为一步，M×N 的图像在窗口大小为f 时Pretest去噪方法的计算规模可降低至O(M×N×f2). 采用该快速方法后本文算法的时间复杂度与此相同。

3 去噪效果对比分析

大多数成像雷达的方位分辨率高于距离分辨率，因此尽管两个方向都可进行多视处理，但一般都选在方位向。目前学术研究中常用的公开PolSAR数据有很多，大多数都是在频域经过多视处理之后的多视复数据。加拿大的机载全极化SAR 系统Convair-580 公开发布的数据距离分辨率约为4 m，方位分辨率约为0.4 m，在对其进行处理前通常先在方位向进行空域的10 视平均，较合适用来测试本算法的实际效果并与其他方法进行对比。

这里使用两组真实的Convair-580 获取的数据进行实验，其中第一组Ottawa 数据是2001年6月26日获得的渥太华地区数据(见图2)，多视处理前数据大小为222×3 429(距离向×方位向)，取其中222×3 420 大小的数据作为实验数据，10 视处理后大小为222×342. 另一组NRCAN 数据来源于加拿大自然资源部(NRCAN)网站(见图3)，因其数据头不全，仅知数据获取于2000年6月20日，具体地点位置并不清楚。其数据大小为1 024×11 000(距离向×方位向)，本文截取其中256×2 560(距离向×方位向)大小的数据作为实验之用，10 视处理后大小为256×256. 选取的区域中有市区、道路、不同类型植被，并且有成对的电线塔架作为大目标以及道路上的车辆作为点目标，十分适于用来主观评价去噪效果好坏。

图2 Ottawa 数据去噪效果对比Fig.2 Comparison of different filters on Ottawa dataset

图3 NRCAN 数据去噪效果对比Fig.3 Comparison of different filters on NRCAN dataset

等效视数(ENL)是评价SAR 数据区域平滑程度的常用指标，其定义为标准差与均值之比。ENL数值越大表示用于计算ENL 区域的平滑效果越好。本文在去噪后的SPAN 数据上计算ENL，并在计算ENL 时为了实验结果更加客观，选择了不同位置的多个同质区块。

在评价去噪算法时只考虑同质区域的平滑效果是不够的，通常在追求同质区域更加平滑、受相干斑影响更小的同时还需要图像的结构信息、细节等有更小的失真。2012年Mittal 等提出了无参考图像的空域评价指标(BRISQUE)［11］，文献［12］将该指标用于PolSAR 图像相干斑抑制效果评价。BRISQUE 可以在空域评价图像的质量，该指标是通过计算图像局部正规化亮度系数的统计信息来评价图像的失真度的，其优点在于无需参考图像，非常适合像SAR 斑点噪声抑制这样没有真实参考图像的问题。因此，本文选择该指标对Pauli 伪彩图进行评价。BRISQUE 的数值在0 ～100 之间，结果越小表示图像的质量越好。BRISQUE 的计算公式如下:

式中:ξ 表示尺度;σ 表示方差;Γ(·)表示Gamma 函数;ψ=σ

本文实验在Intel Core i3 CPU(3.2 GHz)，4G RAM 的环境下进行。实验所用软件为Matlab R2013a 以及PolSARPro 4.2.0. 对比算法包括均值方法(Boxcar)，窗口大小为5;精致极化Lee 滤波［1］，窗口大小为7;Sigma 滤波［2］，Sigma 值为0.9，目标窗口为3，滤波窗口为9;Pretest［8］滤波，窗口大小为3，搜索窗大小为9，阈值ln Ht为-120. 前面3 组对比算法均使用欧洲太空局的PolSAR Pro 软件实现。本文算法中非局部窗口大小为3，搜索窗大小为9，阈值ln Ht为-120，滤波权值计算式中系数α 为2.

两组数据的去噪结果如图2和图3所示。在每组数据的原图中标出了用于测试ENL 值的图块A和图块B. 各种去噪算法的噪声抑制性能以ENL 和BRISQUE 作为标准整理在表1中。

表1 噪声抑制效果对比Tab.1 Comparison of speckle filtering effects of different methods in terms of ENL and BRISQUE

从对比实验可以看出，本文方法在抑制噪声的同时，很好地保持了图像的结构和细节信息。Sigma滤波、Pretest 滤波以及本文方法对同质区域的平滑效果较好，总体大致相当。本文方法与Pretest 方法相比具有相当的同质区域平滑能力，并且图像失真更小。在图像比较复杂的区域，如NRCAN 右下部分以及Ottawa 数据左上部分的城区(住宅区)，都可直观看出本文方法在细节和结构信息保持方面较Sigma 滤波、Pretest 滤波更具优势，其中Sigma 滤波存在“过平滑”的问题。这一点在BRISQUE 值上得到了体现。在两个数据集上本文方法去噪结果的BRISQUE 值比其他方法都要低出许多。而ENL 所体现出来的同质区域的平滑效果则说明了本文方法中相似度计算以及滤波权值计算的合理性。

本文方法对目标特性的保持也较好，例如NRCAN 图像中由左中到右上排成一列的电线塔架区域，由滤波结果可以看出本文方法的去噪结果相比原始图像的失真最小。而观察图中的小目标，例如NRCAN 数据中央部分相互交叉的两条道路上的车辆等，本文去噪结果中这些点目标也得到了很好的保持。另外本文方法对两个数据集中道路边缘的信息保持得也很好，边缘明确并且道路并未被膨胀或腐蚀。以上这些都表明本文方法能够在有效抑制噪声的同时，可以更好地保持图像的结构信息以及细节信息。

PolSAR 去噪算法的另一个关键指标就是对极化相关性保持的能力。为了检测本文算法是否能保持数据的极化相关性，在NRCAN 数据中选取了A、B、C 3 个区域，分别位于植被、电线塔架以及居民区，代表3类典型地物(如图4，因区域较小故用红色实心方块标示)。在原始数据以及本文方法去噪结果数据中分别计算这3 个区域散射矩阵的平均值，并绘制同极化、交叉极化特征图，如图5和图6所示。图5、图6中相同子序号的图像对应同一图块去噪前后的对应同极化或交叉极化特征。对比可见，本文算法去噪前后对各类地物都能很好地保持极化相关性。

图4 用于测试极化特征的图块位置Fig.4 Patches used to test the polarization signature

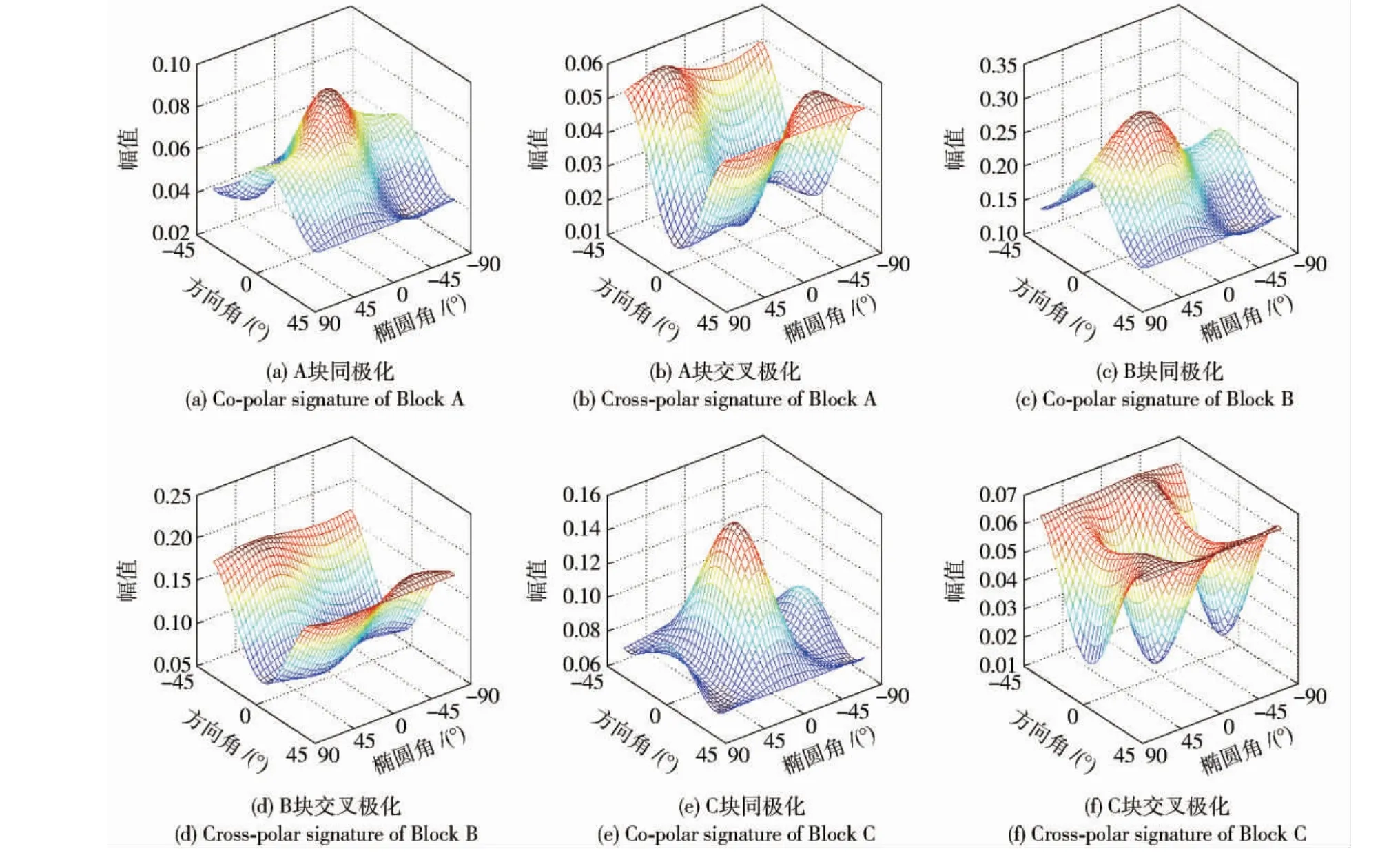
图5 去噪前的同极化与交叉极化特征图Fig.5 The polarization signatures before filtering by the proposed method

4 结论

PolSAR 数据相干矩阵对数累积量的计算方法自2011年提出以来一直是PolSAR 数据处理领域的一个新亮点，但理论研究较多，而在噪声抑制、分割、分类、目标检测识别等应用方向却少有突破。本文将该理论和非局部去噪思想相结合，提出了一种新的PolSAR 去噪算法。新方法使用了相干矩阵的行列式来选择同质区域以及计算相似度，相对于仅使用主对角线上的元素或SPAN 图像更具合理性。本文提出的方法首次直接将复矩阵对数累积量应用于PolSAR 斑点噪声抑制中，文中从噪声平滑、图像保真、极化信息保持三方面对比了新方法与其他Pol-SAR 去噪方法的性能，展现了该方法的特性与优点。本文方法为将PolSAR 数据相干矩阵对数累积量的计算理论进一步应用到PolSAR 数据处理的更多应用提供了参考。

图6 去噪后的同极化与交叉极化特征图Fig.6 The polarization signatures after filtering by the proposed method

References)

［1］ Lee J S，Grunes M R，Grandi G. Polarimetric SARspeckle filtering and its implication for classification［J］.IEEE Transactions on Geoscience and Remote Sensing，1999，37(5):2363 -2373.

［2］ Lee J S，Wen J H，Ainsworth T L，et al. Improvedsigma filter for speckle filtering of SAR imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，47(1):202 -213.

［3］ Vasile G，Trouvé E，Lee J S，et al. Intensity-driven adaptiveneighborhood technique for polarimetric and interferometric SAR parameters estimation［J］. IEEE Transactions on Geoscience and Remote Sensing，2006，44(6):1609 -1621.

［4］ 王爽，于佳平，刘坤. 基于双边滤波的极化SAR 相干斑抑制［J］.雷达学报，2014，3(1):35 -44.WANG Shuang，YU Jia-ping，LIU Kun. Polarimetric SAR speckle reduction based on bilateral filtering［J］.Journal of Radars，2014，3(1):35 -44.(in Chinese)

［5］ Buades A，Coll B，Morel J M. A non-local algorithm for image denoising［C］∥CVPR 2005. San Diego，CA:IEEE，2005:60-65.

［6］ Deledalle C A，Denis L，Tupin F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，18(12):2661 -2672.

［7］ Deledalle C A，Tupin F，Denis L. Polarimetric SAR estimation based on non-local means［C］∥IGARSS 2010. Honolulu，HI:IEEE，2010:2515 -2518.

［8］ Jiong C，Yilun C，Wentao A. Nonlocal filtering for polarimetric SAR data:a pretest approach［J］. IEEE Transactions on Geoscience and Remote Sensing，2011，49(5):1744 -1754.

［9］ Anfinsen S N，Doulgeris A P，Eltoft T. Goodness-of-Fit tests for multilook polarimetric radar data based on the mellin transform［J］. IEEE Transactions on Geoscience and Remote Sensing，2011，49(7):2764 -2781.

［10］ Lee J S. Polarimetric radar imaging［M］. New York:Taylor ＆Francis Group，2009:63 -68.

［11］ Mittal A，Moorthy A K，Bovik A C. No-reference image quality assessment in the spatial domain［J］.IEEE Transactions on Image Processing，2012，21(12):4695 -4708.

［12］ Torres L，Sant’Anna S J S，da Costa Freitas C，et al. Specklereduction in polarimetric SAR imagery with stochastic distances and nonlocal means［J］.Pattern Recognition，2014，47(1):141-157.