自行高炮行进间射击炮口响应特性研究

0 引言

射击线稳定性作为影响自行高炮射击精度的主要原因，在行进间射击过程中受到多种因素的影响。一方面，连续射击载荷作用于火炮身管底部，使后坐部分在一定范围内浮动，后坐力通过摇架，炮塔传递至车体、悬架、轮胎和路面。另一方面，路面不平度激励通过轮胎、悬架、车体传递至炮塔、摇架、炮箱、带炮口制退器的身管。这两种激励使车体与身管在多个自由度上产生振动并相互耦合，影响自行高炮行进间射击线稳定性。另外，在强冲击载荷及路面随机激励条件下，火炮身管柔性、滚珠座圈的接触碰撞等结构非线性因素使身管和底盘的振动特性更为复杂。文献［1 -2］的研究表明，身管柔性和高低机齿弧的接触碰撞在火炮射击时均会对炮口响应产生影响。文献［3］利用Kane-Houston 方法对自行火炮行进间射击建模进行了较为系统研究;文献［4］在自行火炮动力学模型中加入了油气悬挂模型，使计算结果更接近实际;文献［5］通过随机振动理论，提出了路面随机激励下自行火炮随机响应的计算方法。以上研究均未考虑结构非线性的影响。文献［6 -7］分别利用模态展开法描述构件变形和建立自行火炮渐开线直齿轮-齿弧精确三维接触模型，研究了火炮射击时身管柔性和齿轮-齿弧接触等结构非线性对炮口振动的影响。但仅对大口径火炮停止状态下射击时炮口扰动进行了研究。

本文以轮式某自行高炮为研究对象，建立了某自行高炮行进间发射动力学模型，综合考虑了刚柔耦合、大规模接触碰撞因素，研究了轮式自行高炮行进间射击时，行驶速度，路面条件，发射载荷以及结构非线性因素对炮口扰动的影响规律。

1 行进间发射动力学模型

1.1 轮式自行高炮拓扑结构

自行高炮主要包含行驶机构和火力部分，并以上下座圈相连接。行驶机构由轮胎、悬架、车体、动力总成和转向机构等部件组成，8 个车轮通过悬架与车体连接，其中左前、左二、右前、右二悬架为麦弗逊悬架，左三、左后、右三、右后悬架采用油气悬架，其他部件质量及转动惯量通过计算等效至车体。

火力部分由炮塔、摇架、炮箱、带炮口制退器的身管等组成，炮塔与上座圈、车体与下座圈采用固定连接，上、下座圈与201 个滚珠定义接触碰撞关系，使炮塔可绕回转中心转动。耳轴和轴承分别与摇架、炮塔固定连接，摇架通过耳轴安装定位在炮塔上并通过旋转副定义二者之间的转动关系，起落部分可绕耳轴轴线转动，同时建立高低机主齿轮与摇架齿弧的接触碰撞。身管为弹性体，取前80 阶模态坐标描述其弹性变形，炮口制退器与身管通过前端界面节点刚性连接，身管与炮箱通过后端界面节点固定连接且与摇架之间定义滑移副，并在相应位置建立弹性元件模拟复进簧，当连续射击载荷作用于身管时，后坐部分在一定范围内浮动。全炮含244 个刚体和1 个弹性体，9 个滑移铰、1 个旋转铰、5 个固结铰。整个系统共有1 264 个运动自由度和80 个变形自由度。利用铰描述各部件之间的连接关系，包括运动副、接触碰撞、弹性元件、力元等，用hi(i=1，2，…，432)表示，其中hr、ht、hf分别表示旋转铰、滑移铰和固结铰。全炮拓扑结构如图1所示。

图1 自行高炮行进间射击拓扑结构Fig.1 Topology of antiaircraft gun firing on the move

1.2 路面不平度模型

路面不平度是自行高炮行驶时影响射击线稳定性的主要因素，可通过路面功率谱密度描述其统计特性，国家标准GB7031—2005 中对路面不平度功率谱采用(1)式拟合［8］:

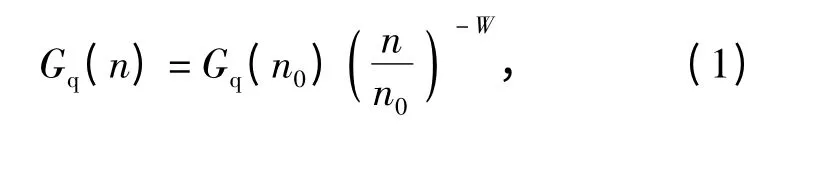
式中:n 为空间频率有效频带中的某一空间频率;n0为参考空间频率，n0=0.1 m-1;Gq(n0)为参考空间频率n0下的路面功率谱密度值;W 为频率指数，决定了功率谱密度的频率结构，W=2.

试验证明路面不平度是平稳的、各态历经、均值为0 的高斯过程，可通过谐波叠加法对路面不平度进行重构。谐波叠加法以离散谱逼近目标随机过程的随机模型，将随机路面不平度假设为多个含有随机相位的三角函数叠加，理论严密，简单直观，适用于任意随机路面的模拟，具有良好的适应性和高精度。当自行高炮以车速u 在空间频率为n 的路面上行驶时，可根据时间与空间频率转换关系f =un 将空间频率n1＜n ＜n2范围内的路面功率谱密度Gq(n)转换为时间频率f1＜f ＜f2内的路面功率谱密度

将f(f1≤f≤f2)划分为N 个区间，用每个区间的中心频率fi(i=1，2，…，N)处的谱密度值Gq(fi)代替Gq(f)在整个小区间内的值，则可以在时间域内用三角级数模拟随机路面不平度

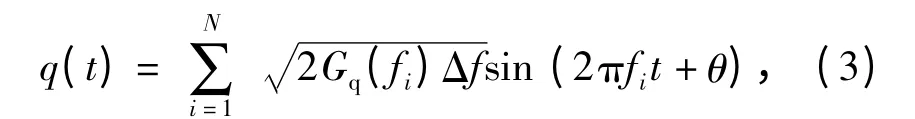
式中:θ 为［0，2π］的随机数。

将(3)式转换为空间域内谐波叠加式)

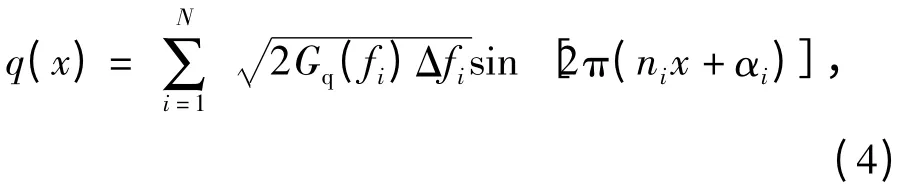
式中:αi为［0，1］的随机数;x 为路面在X 方向上的长度。

运用上述模型，结合自行高炮实际行驶工况，利用Matlab 数学工具编写路面谱程序，重构了符合我国道路分级标准的B、C、D 级路面，对长150 m，宽6 m的自行火炮行驶道路进行模拟，路面高程随距离L 变化如图2所示(取前20 m)。

1.3 柔性身管模型

为了得到身管模态参数，利用Hypermesh 建立身管有限元模型。针对身管的结构特点，利用8 节点六面体等参单元对身管进行有限元离散，通过模态综合方法获得身管自由状态下的模态参数，在ADAMS 中通过界面节点与炮箱、炮口制退器连接，从而确定其边界条件。身管有限元模型共有15 962 个节点，12 674 个单元，图3为身管第1、3、5、7 阶振型。

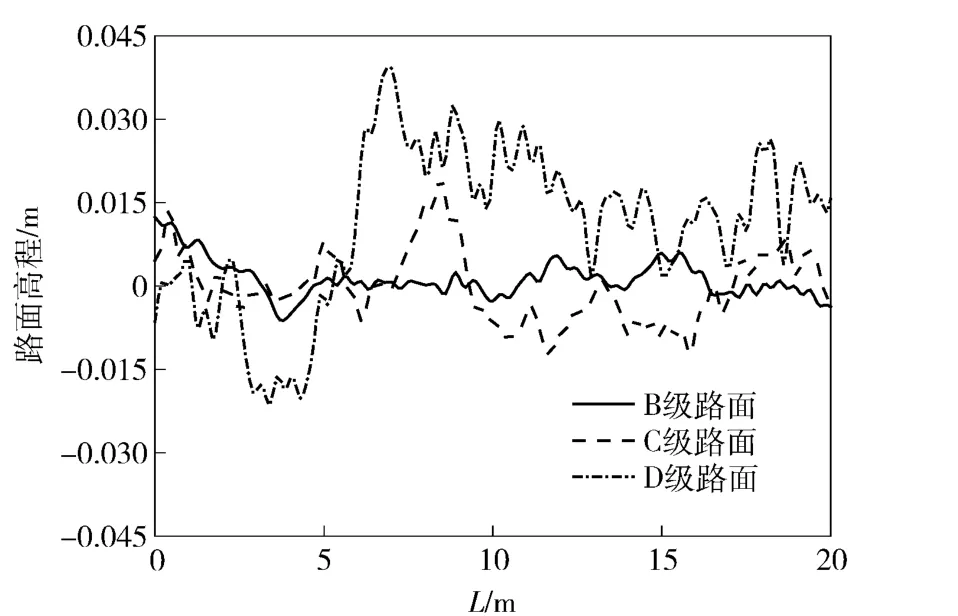
图2 路面不平度曲线Fig.2 Curves of road irregularities

图3 柔性身管各阶振型Fig.3 Vibration mode of flexible barrel

对于实际工程有意义的模态大多为低频部分，根据各阶模态质量在总模态质量中所占的份额和各阶模态惯矩在总模态惯矩中所占的份额大小来决定该阶模态的取舍。将截取的身管80 阶模态集作为主模态，其中前10 阶固有振动频率如表1所示。

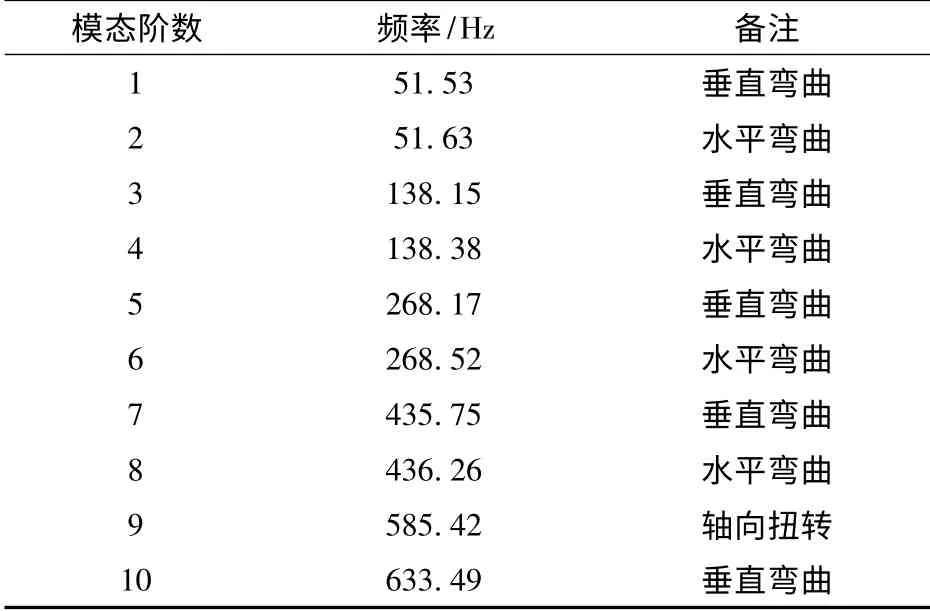
表1 身管前10 阶模态频率Tab.1 The first 10 order modal frequencies of barrel

1.4 滚珠座圈接触碰撞模型

轮式自行高炮的滚珠座圈作为回转/支承机构，赋予火力部分方向射角并支撑火力部分重量。火炮射击时，强冲击载荷通过轴承上座圈、滚珠、下座圈之间的接触碰撞传递至车体，引起车体在多个自由度上的振动响应。

滚珠轴承依靠内外滚道和滚珠的相互接触来支承载荷，接触力F 可根据Hertz 理论F=kδ1.5计算得到，其中k 是接触刚度系数，δ 是变形量。内、外滚道与滚珠的接触刚度［9］为

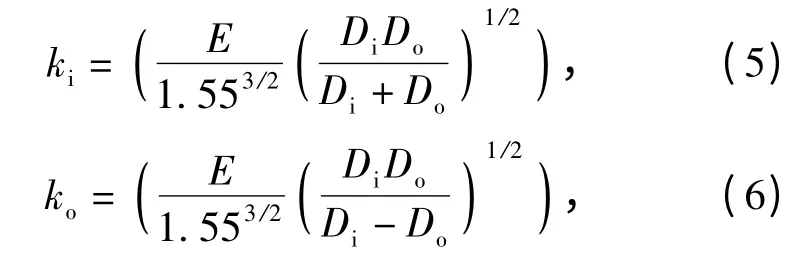
式中:E 为座圈材料的杨氏模量;Di、Do分别为内、外滚道直径。

滚珠与滚珠的接触刚度直接由Hertz 公式估算:

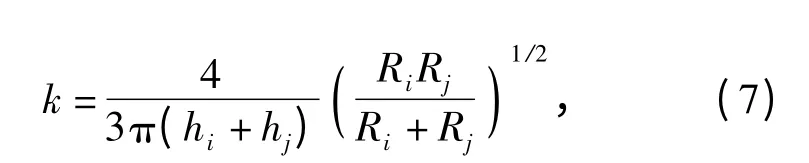
式中:Rl(l=i，j)为滚珠半径;为材料的泊松比，El为滚珠材料的杨氏模量。

自行高炮座圈滚珠数量较多，接触/碰撞定义工作繁琐复杂，为了方便处理滚珠与上下座圈的大规模接触问题，在ADAMS 环境下通过二次开发，编译宏命令程序完成滚珠的编号、装配定位、刚体定义和接触参数定义等工作。

如图4所示，建模时可通过程序生成的对话框，对滚珠座圈大规模接触模型进行直观、快速的定义和修改。通过运行宏命令，建立201 个滚珠与上、下座圈大规模接触模型并定义滚珠与滚珠以及滚珠与上、下座圈之间的接触/碰撞关系。

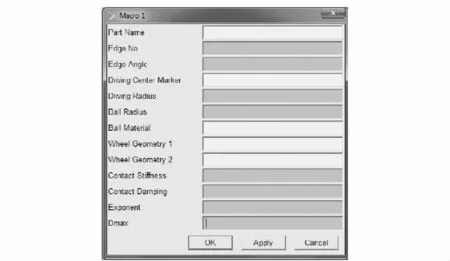
图4 滚珠与上、下座圈接触模型定义界面Fig.4 Defined interface of ball and bearing contact model

2 数值计算与分析

2.1 模型验证

为验证发射动力学模型的正确性，设定某轮式自行高炮置于刚性水平路面并处于制动状态，车轮与地面无相对滚动(停止状态)，并将计算结果与试验测试结果对比。试验采用电涡流位移传感器，测试射击时炮口制退器后方200 mm 处身管上测点的高低方向位移，表2为0°射角、正装药、10 连发射击时，计算所得的测点高低方向位移和试验测试值对比。

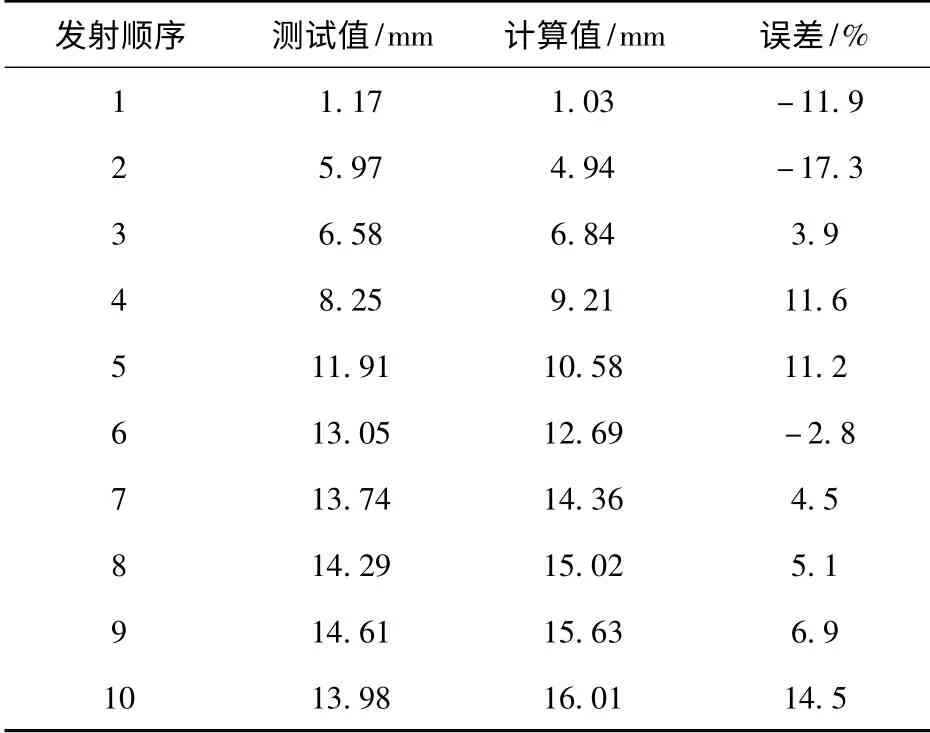
表2 10 连发射击载荷作用下测点高低角位移计算与测试值对比Tab.2 Comparison between calculated and test vertical displacements under 10 bursts-of-launch load

通过对比发现，测点高低方向位移计算结果与实际测试数据基本一致，说明轮式自行高炮在刚性水平地面、0°射角条件下的发射动力学模型具有一定准确性，为进一步分析不同行驶工况和射击工况对炮口响应特性的影响提供了依据。

2.2 行驶工况的影响

为分析不同路面条件和行驶速度对炮口响应的影响，结合实际工况，应用建立的自行高炮行进间发射动力学模型，计算其在B、C、D 级路面上以15 km/h和30 km/h 时速行进间射击时的炮口动态响应。针对自行高炮启动、加速并完成射击的整个12 s 过程，设置相应计算时间，计算步长为0.1 ms.动力学计算开始前对自行高炮进行静平衡分析，获得其静平衡位置。经多次试算发现，动力学计算开始后3 s 内自行高炮处于加速阶段，为充分考虑不同行驶工况对炮口扰动的影响，自行高炮需要在相应等级的起伏路面上保持匀速行驶一段时间后实施射击，故射击载荷于第8 s 开始加载，整个10 连发射击过程持续0.6 s，分析仅针对自行高炮达到匀速行驶状态后，行进间射击时的炮口响应。

图5和图6分别为自行高炮15 km/h 和30 km/h时速下，以0°射角进行10 连发射击的炮口高低角位移曲线。计算结果表明，相同行驶速度下，随着路面不平度增大，炮口扰动明显增大。同一路面上，行驶速度的提高也会使炮口扰动呈现增大趋势。

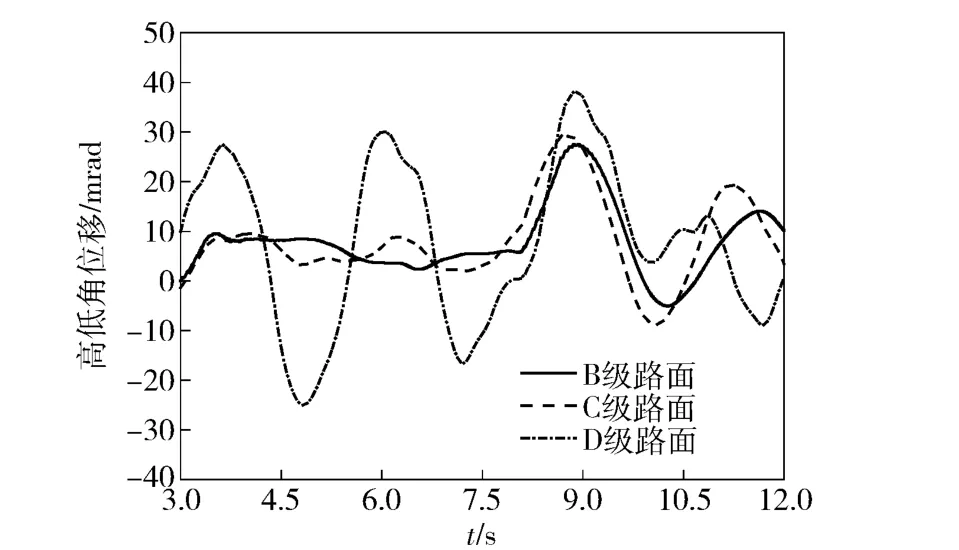
图5 15 km/h 时速行进间射击炮口高低角位移Fig.5 Elevation angles of muzzle firing on the move at 15 km/h

图6 30 km/h 时速行进间射击炮口高低角位移Fig.6 Elevation angles of muzzle firing on the move at 30 km/h

表3为各行驶工况下，10 连发射击后的炮口最大高低角位移。自行高炮在B 级路面上以15 km/h时速行驶并实施射击时的炮口最大高低角位移为27.52 mrad，而在C、D 级路面上行驶时，炮口最大高低角位移达到28.85 mrad 和38.17 mrad，分别增大了4.83%和38.69%.在相同路面条件下，行驶速度的提高会使炮口响应增大，自行高炮在B 级路面上行驶速度从15 km/h 提高至30 km/h，射击时的炮口最大高低角位移增大了25.47%.

表3 不同行驶条件下炮口最大高低角位移Tab.3 Maximum angular displacements of muzzle at different driving conditions

2.3 射击工况的影响

自行高炮射击工况复杂多样，针对典型射击工况，利用建立的自行高炮行进间发射动力学模型，分别计算5、10 连发射击条件下，以0°、45°、80° 3 种射角行进间射击时的炮口动态响应，连续射击载荷于自行高炮行驶至第8 s 时开始加载。图7和图8为自行高炮以15 km/h 时速在B 级路面上实施行进间射击时，不同射击工况下的炮口高低角位移随时间变化曲线。

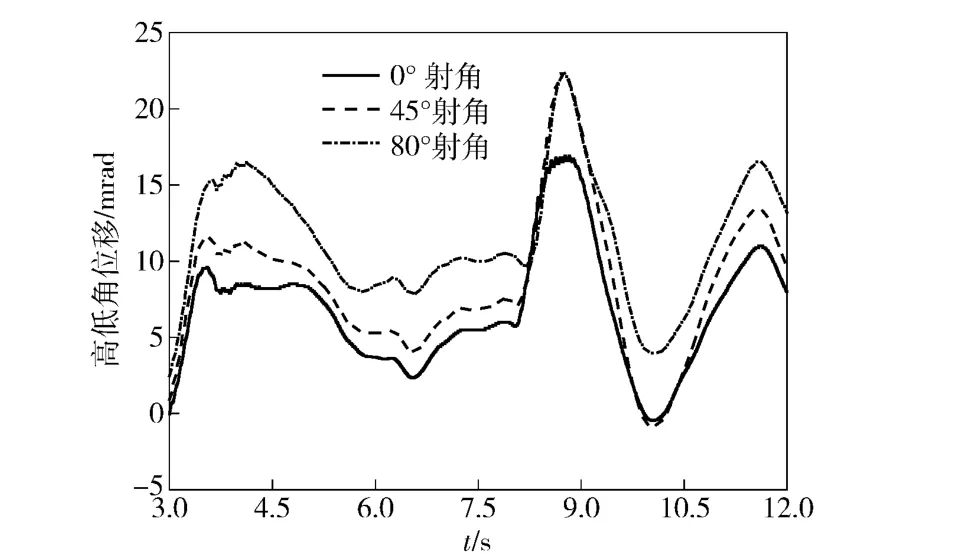
图7 行进间5 连发射击炮口高低角位移Fig.7 Elevation angles of muzzle firing on the move under 5 bursts-of-launch load

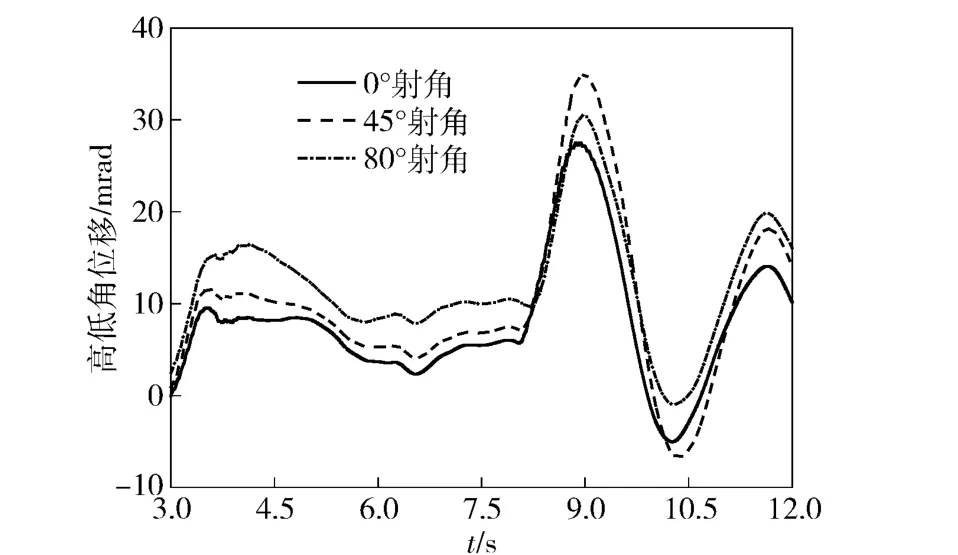
图8 行进间10 连发射击炮口高低角位移Fig.8 Elevation angles of muzzle firing on the move under 10 bursts-of-launch load

计算结果表明，随着射角增大，射击开始前的炮口扰动相应变大。自行高炮行驶至第8 s 开始射击时，0°射角炮口高低角位移为5.84 mrad，而以45°和80°射角射击时，炮口高低角起始位移为7.29 mrad和10.35 mrad，分别增大了22.4%和77.2%.

表4为每一发弹丸出炮口瞬间的炮口高低角位移。从表4可以发现，射击开始后，连续射击载荷作用下，不同射击工况的炮口响应变化明显不同，5 连发射击时，0°和45°射角下的炮口响应持续增大，其中0°射角时的炮口响应变化最为剧烈，每发相比前一发增大的平均值为1.33 mrad，而45°射角时仅为0.82 mrad.80°射角时，炮口响应则保持在一定范围内，稳定性较好。10 连发射击时，从第6 发开始，3 种射角下的炮口响应均呈增大趋势，但仍以0°射角时的炮口响应增大最为明显。

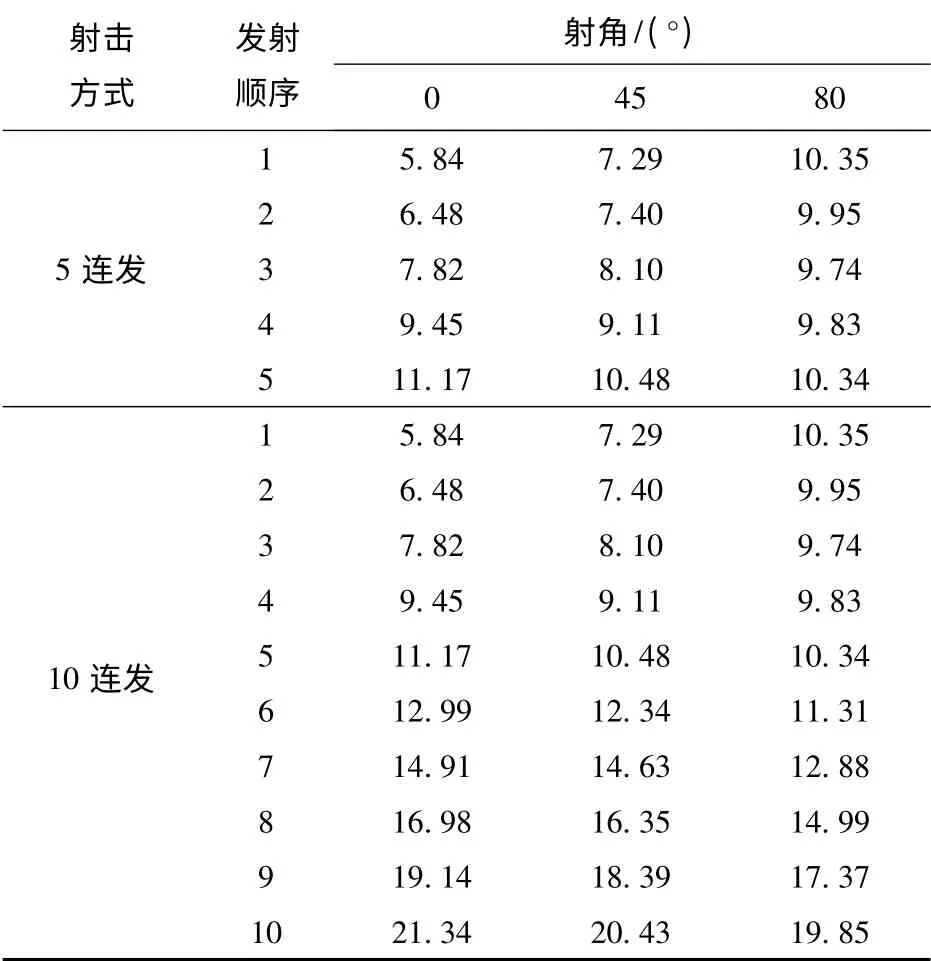
表4 不同射击方式下炮口高低角位移Tab.4 Angular displacements of muzzle at different launch modes mrad

综上所述，当射角增大，炮口扰动减小。这主要是由于随着射角增大，射击载荷对于车体的翻转力矩减小，车体稳定性变好。由此可见，行进间射击时不同射角和射击方式会对炮口响应产生不同程度的影响。

3 结论

本文应用多体系统动力学、车辆地面力学和火炮发射动力学，综合考虑了刚柔耦合和接触碰撞两种结构非线性因素，建立了轮式自行火炮行进间发射动力学模型，综合分析了行驶工况、射击工况对行进间射击时炮口扰动的影响。数值计算结果表明:

1)随着行驶速度的提高和路面不平度增大，轮式自行高炮射击时的炮口扰动增大，在B、C、D 3 种等级路面上，行驶速度从15 km/h 提高至30 km/h时，炮口最大高低角位移分别增大了25.47%、23.54%和11.92%.

2)相比小射角工况，大射角工况下的炮口扰动受车速和路面条件的影响更为明显，但在连续射击时，炮口扰动要小于小射角工况。

本研究为掌握轮式自行高炮行进间射击时炮口响应规律提供了参考依据。

References)

［1］ 闵建平，陈运生，杨国来.身管柔性对炮口扰动的影响［J］.火炮发射与控制学报，2000(2):28 -31.MIN Jian-ping，CHEN Yun-sheng，YANG Guo-lai.Impaction of flexible tube on muzzle vibration［J］.Journal of Gun Launch ＆Control，2000(2):28 -21.(in Chinese)

［2］ 曾晋春，杨国来，王晓锋.考虑轴承接触/碰撞的某火炮动力学数值仿真［J］.火炮发射与控制学报，2010(3):30 -33.ZENG Jin-chun，YANG Guo-lai，WANG Xiao-feng.Dynamicsnumerical simulation for a certain gun in consideration of contact/impact among parts in traverse bearing［J］.Journal of Gun Launch＆Control，2010(3):30 -33.(in Chinese)

［3］ 冯长根，温波，李才葆.自行火炮行进间射击动力学研究［J］.兵工学报，2002，23(4):457 -461.FENG Chang-gen，WEN Bo，LI Cai-bao.Dynamic analysis of a self-propelled gun firing on the move［J］.Acta Armamentarii，2002，23(4):457 -461.(in Chinese)

［4］ 程刚，张相炎，董志强，等.轮式自行高炮行进间射击稳定性仿真研究［J］.兵工学报，2010，31(2):149 -153.CHENG Gang，ZHANG Xiang-yan，DONG Zhi-qiang，et al.Simulation research on the stability of firing on the move for wheeled self-propelled anti-aircraft gun［J］.Acta Armamentarii，2010，31(2):149 -153.(in Chinese)

［5］ 闵建平，谭俊杰，李剑锋.行进间射击时的动力学研究［J］.振动与冲击，2003，22(4):88 -90.MIN Jian-ping，TAN Jun-jie，LI Jian-feng.Impaction of flexible tube on muzzle vibration［J］.Journal of Vibration and Shock，2003，22(4):88 -90.(in Chinese)

［6］ 吴参，王维锐，陈颖，等.三维路面谱的仿真建模与验证［J］.浙江大学学报:工学版，2009，43(10):1935 -1938.WU Can，WANG Wei-rui，CHEN Ying，et al.Simulation and validation of three dimensional road surface spectrum［J］.Journal of Zhejiang University:Engineering Science，2009，43 (10):1935 -1938.(in Chinese)

［7］ 曾晋春，杨国来，王晓锋.计及齿轮-齿弧接触的火炮动力学分析［J］.弹道学报，2008，20(2):81 -84.ZENG Jin-chun，YANG Guo-lai，WANG Xiao-feng.Dynamics analysis for gun with consideration of contact between arc and gear［J］.Journal of Ballistics，2008，20(2):81 -84.(in Chinese)

［8］ GB/T 7013—2005 机械振动道路路面谱测量数据报告［S］.北京:中国标准出版社，2005:37 -63.GB/T 7013—2005 Mechanical vibration-road surface profiles reporting of measured data［S］.Beijing:Standards Press of China，2005:37 -63.(in Chinese)

［9］ 冈本纯三.球轴承的设计［M］.黄志强，罗继伟，译.北京:机械工业出版社，2003:32207.J Yunzo Okamoto.Ball bearing design［M］.HUANG Zhi-qiang，LUO Ji-wei，translated.Beijing:China Machine Press，2003:32207.(in Chinese)