基于直线稀疏光流场的微小型无人机姿态信息估计方法研究

关震宇，李杰，杨欢，徐蓓蓓，刘畅

(北京理工大学 机电学院，北京100081)

0 引言

微小型无人飞行器(MAV)并不是常规飞行器的简单缩小，由于受到体积和载荷重量等方面的限制，其在结构设计、气动设计、动力系统和导航控制方法等方面与传统飞行器存在较多不同。尺寸的微小化对飞行器姿态测量系统的设计提出了挑战，传统的高精度、低漂移的陀螺由于体积和重量的原因并不适合微小型飞行器使用，而基于微机电技术开发的微陀螺和微加速度计等器件受限于现有的精度、稳定性、温漂等因素制约，在长期使用时会产生较大的积累误差［1］。由于上述传统器件的局限性，需要探索一种新型的微小型飞行器姿态信息估计方法对传统方法进行替代和补充。

早期飞机并没有复杂的传感系统，飞行员对于飞机姿态的获取直观地来源于其视野中地平线位置的变化;由于任务使命的关系，MAV 通常携带有摄像设备进行侦察和航拍作业，在侦察相机的视场中，地平线又是自然界最明显的标志物，因此借助地平线位置来测量飞行器姿态就成为了一种可行的思路。目前关于地平线的各种提取方法已经相当成熟，可以分为基于边缘特征的地平线提取［2-3］、基于区域统计特征的地平线提取［3-4］和基于机器学习的地平线提取［5］;在使用地平线信息进行姿态角计算方面，同样开展了大量的研究工作。参考文献［6 -7］通过地平线与图像水平线夹角进行飞行器滚转角估计，参考文献［8 -9］使用分割后天地各自的质心位置来估算滚转角，并使用天地分割线两侧面积的变化来估计飞行器的俯仰角，参考文献［3］也采用了类似的方法来估计俯仰角，但天地线两侧面积比例会由于滚转角的变化而发生较大的变动，因此会对俯仰角的估计带来不小的估计误差，参考文献［10］具体指出了这一点问题，并提出上述方法甚至可能会造成严重的飞行事故。参考文献［11］使用了摄像机模型对俯仰角和滚转角的计算进行了理论推导，提出了一种基于直线模型的俯仰角和滚转角的计算方法，但不足之处在于该方法需要预先对所使用摄像机进行标定获取其内参数矩阵，而且从其仿真结果来看该方法测量精度不高。除此之外，上述所有方法都只能计算飞行器的俯仰角和滚转角，对于飞行器俯仰角速度、滚转角速度和偏航角速度等重要姿态参数或无法直接测量，或需要通过差分运算进行估计，在实际使用中存在一定的局限性。参考文献［12］针对上述局限提出了一种基于光流的滚转角速度和俯仰角速度提取方法，但该方法需要计算图像全局光流场，由于全局光流场的计算量较大，因此该方法在实时应用方面存在问题。参考文献［13］总结了基于视觉的无人飞行器姿态估计方法，指出基于光流的估计方法可以实现俯仰、滚转和偏航3 个通道姿态信息的估计。

为了克服上述不足，本文提出了一种图像中的直线稀疏光流场计算方法，并在此基础上提出了基于直线稀疏光流场的飞行器姿态信息估计方法。该方法可以用于无法安装微机电陀螺的微小型飞行器进行姿态信息获取，也可以通过与传统导航手段进行融合，辅助飞行器进行导航控制。该方法不依赖计算图像的全局光流，仅需要计算地平线附近的稀疏光流，从而降低了算法计算量。经过理论推导与仿真分析，该方法可以有效地对飞行器俯仰角速度、滚转角速度和偏航角速度等姿态信息进行估计，并在飞行器角速度较低的情况下具有较高的精度。

1 直线稀疏光流场的定义与提取算法

光流的概念最早由Gibson 于1950年提出，是指图像中模式运动的速度。光流场是一种二维(2D)的瞬时速度场，其中2D 速度矢量是景物中可见的三维速度矢量在成像表面的投影［14］。光流计算是由Horn 等［14］首先提出，之后出现了一系列的有关全局光流计算方法［15-18］。全局光流理论上可以估计出图像上每一个像素点的光流矢量值，其不足之处在于需要大量的迭代计算来获取，算法时间效率不高，且易受到图像局部噪声的影响。为了解决上述问题，稀疏光流场的概念应运而生。目前文献中常涉及的稀疏光流场主要指角点的稀疏光流场，其获取方法首先使用基于特征的方法对相邻两幅图像进行角点匹配，随后使用匹配角点的运动矢量来近似替代其光流矢量。这种计算方法相较于全局光流计算具有运算速度快、对噪声不敏感等优点，其缺点是仅能获得图像中局部(角点处)的光流信息，但因为角点作为图像中重要的特征，它的局部光流也含有重要信息，因此稀疏光流场在图像识别、运动检测、目标提取等方面具有广泛应用。

所谓直线稀疏光流场，就是在角点稀疏光流场基础上提出的一种图像稀疏光流场，它是指相邻两帧图像中共线点的光流矢量的集合，如图1所示。与角点稀疏光流场不同的是，直线稀疏光流场是通过提取两帧图像中相匹配的直线，并通过计算直线上每一个点的运动矢量而获得的。因为图像中的边缘信息常用直线描述，因此直线稀疏光流场就特别适合描述图像中边缘的变化。

图1 直线稀疏光流场定义Fig.1 Sparse line-optical flow field

直线稀疏光流场的计算方法如下:

设摄像机几何模型为透视模型，建立OXYZ 空间坐标系，oxy 为图像坐标系，o 为摄像机光心，光轴与Z 轴重合，图像坐标系原点设为在OXY 坐标系(0，0，f)处，其中f 为焦距，x 轴和y 轴分别与X 轴和Y 轴平行，如图2所示。

在成像平面上，Li+1和Li是空间一条直线在成像平面的连续两帧投影，p 是空间一点P 在成像平面上的投影。对于直线Li上一点pi，其在直线Li+1对应点计为pi+1.

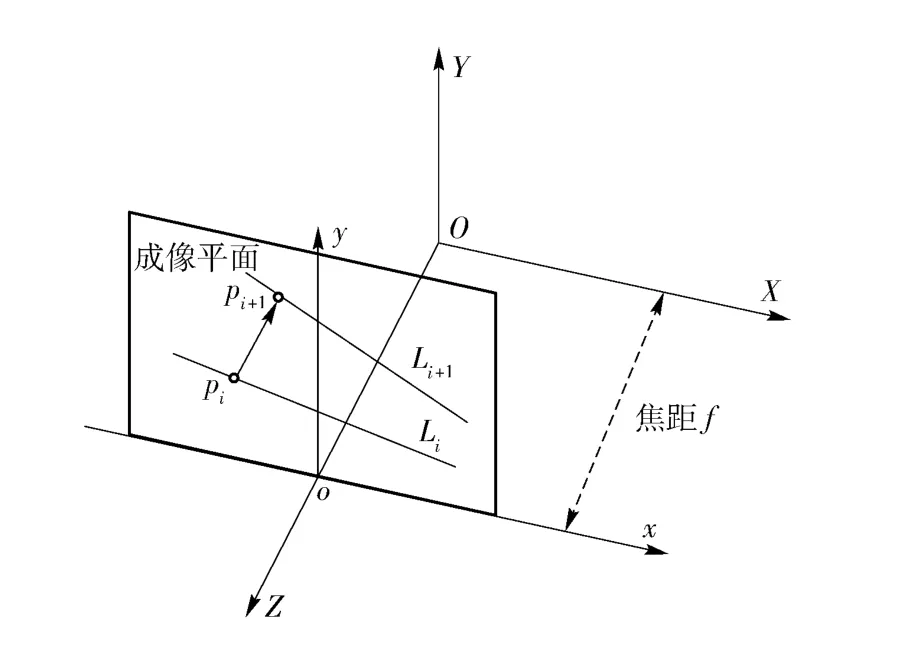
图2 摄像机透视投影模型Fig.2 Camera perspective projection model

不失一般性，设f=1，对于该摄像机模型有

对空间一点P=(X，Y，Z)T，其在成像平面投影p=(x，y)T，点P 在空间的运动满足如下运动方程:

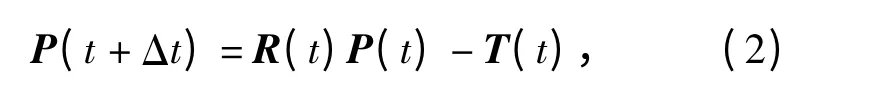
式中:矩阵R 和矩阵T 分别描述点P 的旋转运动和平移运动;Δt 为两帧图像间的时间间隔，当Δt 很小时，可对(2)式作如下近似:

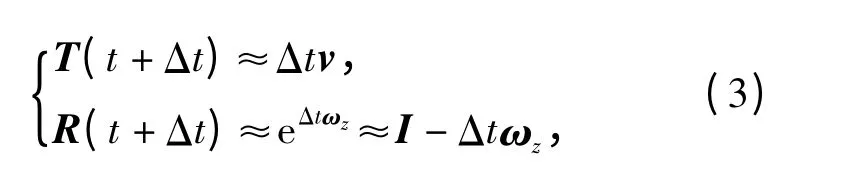
式中:v = (v1，v2，v3)T，ωz分别表征P 点的平移速度矢量和绕光轴逆时针方向的旋转角速度矩阵，将其代入(2)式，得

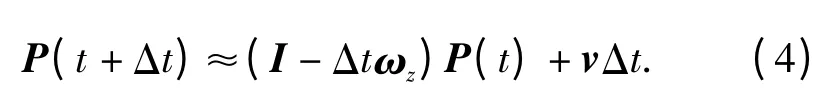
经整理，即可得

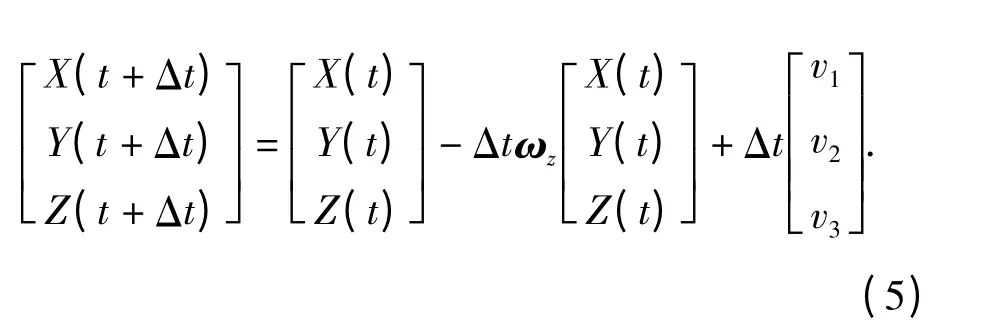
展开(5)式最后一行，得

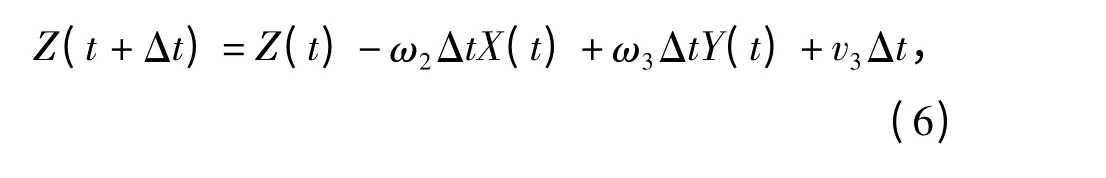
则

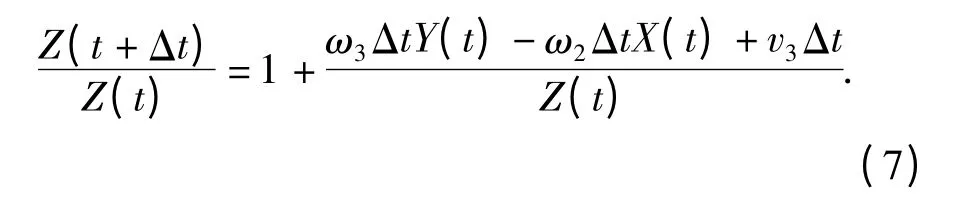
当点P 沿光轴的运动相比于点P 到光心的距离非常小时，即满足

时，有

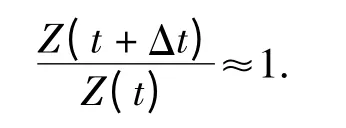
此时，对(5)式两边同除Z(t)，

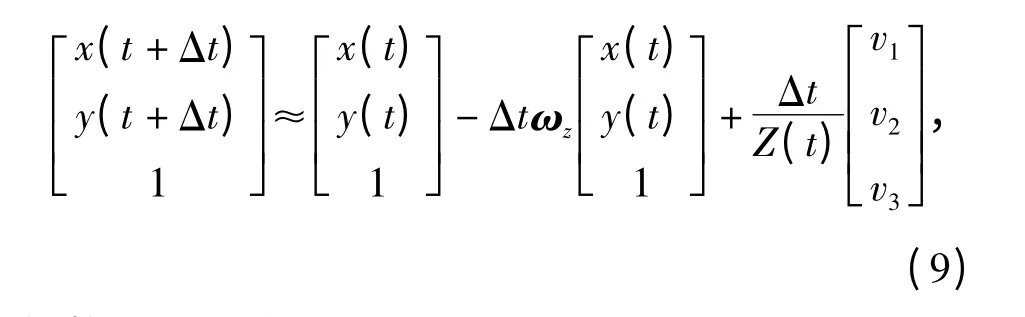
经整理，即可得

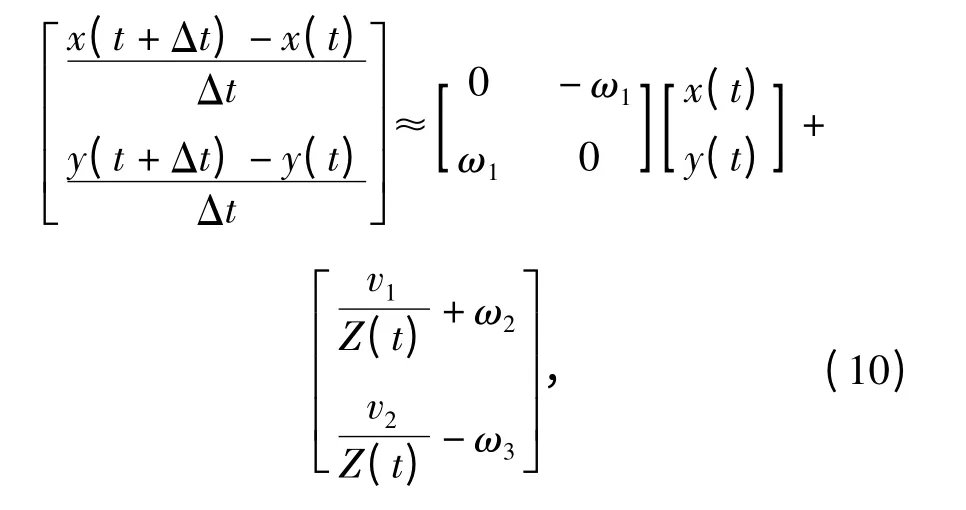
则有

式中:w(x，y，t)表示图像上p 点在t 时刻的二维运动速度，即时变图像的光流，这样就建立了图像上点位移场与光流场之间的关系。

在图像坐标系下，设直线Li和Li+1的直线方程分别为

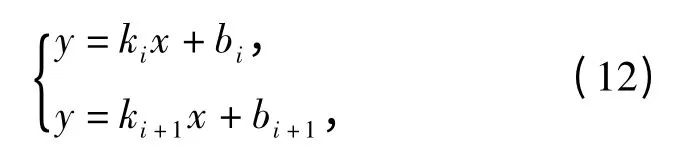
式中:ki、bi、ki+1、bi+1分别为直线Li、Li+1的斜截式直线方程参数。点pi和点pi+1的坐标分别为(xi，yi)，(xi+1，yi+1).

点pi处图像灰度满足光流恒等式为

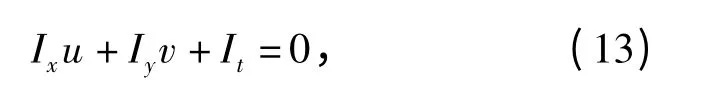
式中:Ix、Iy、It分别是图像上(xi，yi)点处的灰度值在x、y、t 3 个方向上的差分值。

对于连续的第i 帧和第i +1 帧图像，点pi的稀疏光流场为

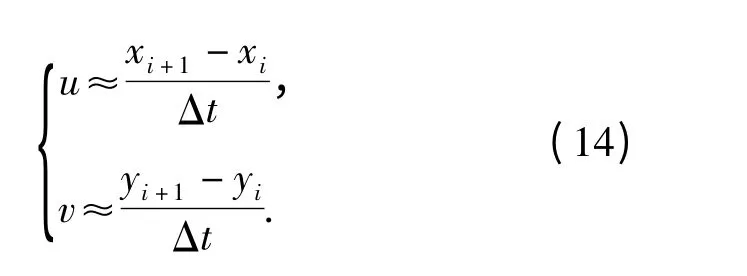
联立(12)式、(13)式、(14)式，得

式中:除(xi+1，yi+1)坐标外，其余均为已知。求解(15)式并代入(14)式即可求取点(xi，yi)处的光流矢量:

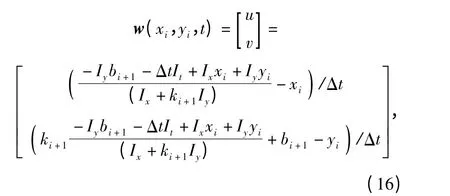
遍历直线Li上的点，即可计算出对应的直线稀疏光流场。

2 基于直线稀疏光流场的飞行器姿态测量

在无人机航拍图像中，地平线往往是最明显的标志物，在图像经过地平线提取算法处理后，地平线更是可以成为视野中唯一的直线，因此特别适合使用直线稀疏光流场对于其运动进行分析。本文将使用地平线附近的稀疏光流场作为例子说明基于直线稀疏光流场的飞行器姿态测量方法。

在图2模型的基础上建立地平线的投影关系模型，如图3所示，建立大地坐标系OwXwYwZw，机体坐标系OXYZ，图像坐标系oxy，大地坐标系是以地平线上一点Ow为原点建立的右手系，取竖直向上方向为Yw轴，地平线方向为Xw轴;摄像机与机体头部固定连接，以摄像机光心O 为原点建立右手系OXYZ，其中Z 轴与光轴重合，取竖直向下方向为Y轴。在焦平面建立图像坐标系oxy，以图像中心为原点o，x 轴和y 轴分别与OXYZ 坐标系的X 轴和Y轴平行。

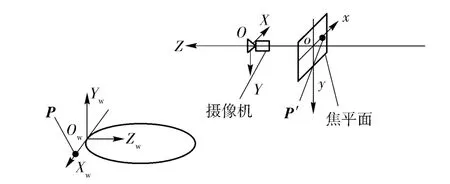
图3 地平线投影模型Fig.3 Horizon projection model

以坐标系OXYZ 为惯性参考系，在地平线上任取一点P，设其在OXYZ 坐标系下坐标为P(X，Y，Z)，其在焦平面上的对应点为p'(x，y，z)，则点P(X，Y，Z)的运动方程可描述为

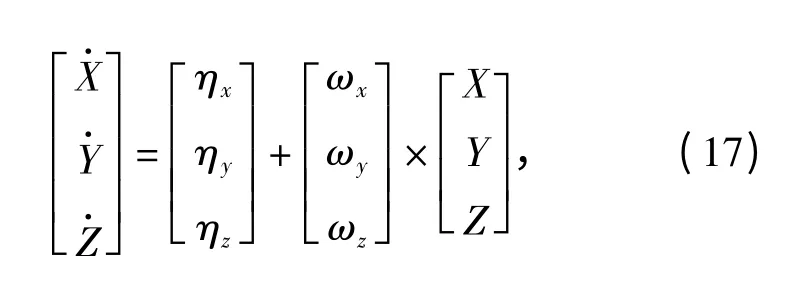
式中:ηx、ηy、ηz是点P 的平移运动参数;ωx、ωy、ωz是飞行器滚转角速度。分别表征俯仰角速度、偏航角速度和滚转角速度。

将(1)式代入(17)式，得

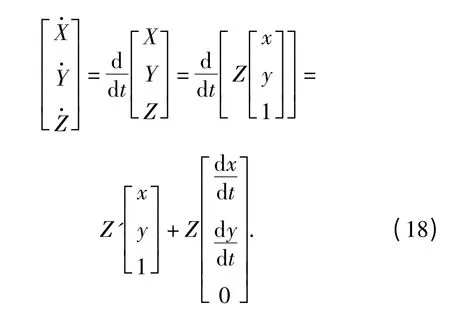
由于地平线距离很远，因此在本模型中，可认为(8)式中条件可以得到满足，这样由(11)式可得

将(19)式代入(18)式，得

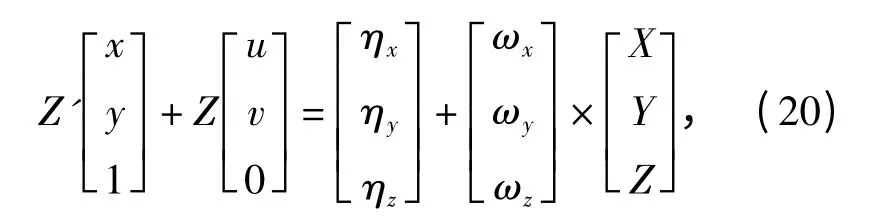
对(20)式整理得

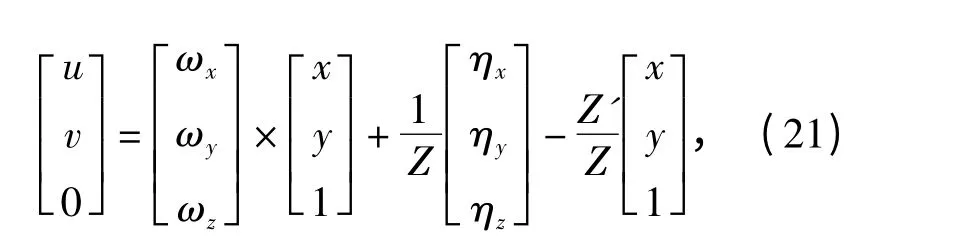
消去Z'得

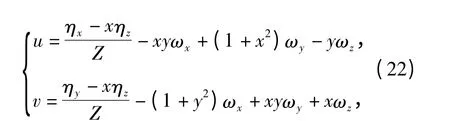
即可建立光流场与图像运动之间的关系。

因为点P 在地平线上，而地平线距离观察点的距离可近似为无穷远，因此可以近似看作Z→∞，因此消去(22)式中含Z 项，即可得

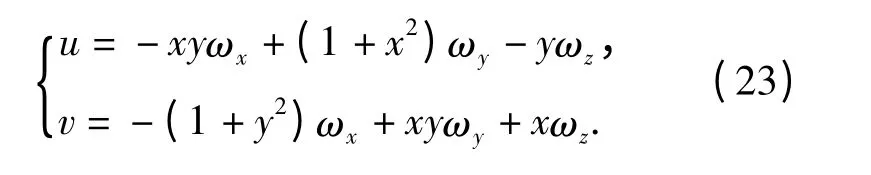
(23)式是一个关于ωx、ωy、ωz的线性方程组，只要获取不少于地平线上不少于3 个点的光流矢量值，即可解算出飞行器的3 个角速度。

特别说明的是，本文虽然以地平线作为研究对象说明基于直线稀疏光流场的飞行器姿态测量方法，但是本方法并不局限于地平线存在的情况，只要无人机摄像机视场中存在典型直线特征(如机场跑道、道路、楼宇等)，本方法同样适用。

3 仿真与实验

3.1 直线稀疏光流场计算仿真

使用连续两帧测试图像对于直线稀疏光流场的计算进行仿真，测试图像如图4所示，大小为416×240 像素，黑白图像。两帧图像帧间为0.04 s，首先使用Sobel 算子对两幅图像进行边缘提取，如图5所示。

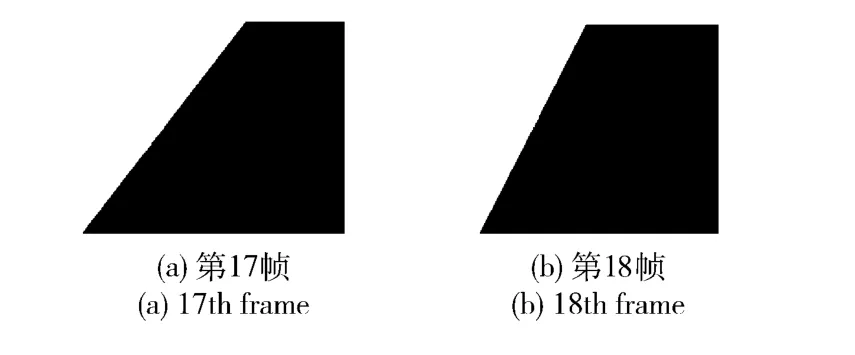
图4 连续两帧测试图像Fig.4 Two consecutive images

对第17 帧和第18 帧图像使用第2 节中直线稀疏光流场提取算法计算直线稀疏光流场，(16)式中Ix、Iy、It的计算采用如下差分格式:

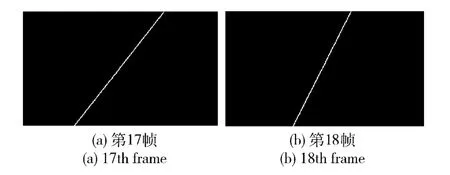
图5 测试图像边缘提取的结果Fig.5 Edge extraction of test images

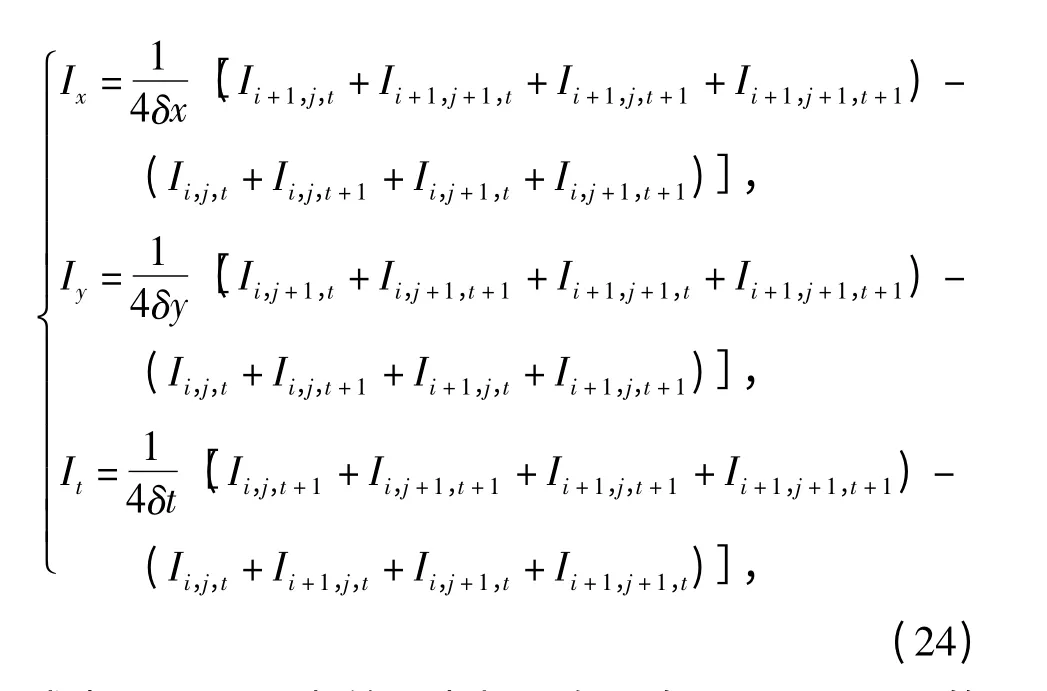
式中:δx、δy、δt 为差分步长。在配备Intel i7 CPU 的计算机上，使用MatLab2012 平台进行数值仿真，计算出的直线光流场如图6所示，耗时0.223 6 s. 由于没有该图像的标准光流场可以对比，使用Horn 方法在同样平台上计算第17 和18 帧全局光流场，耗时3.704 4 s，如图7所示。

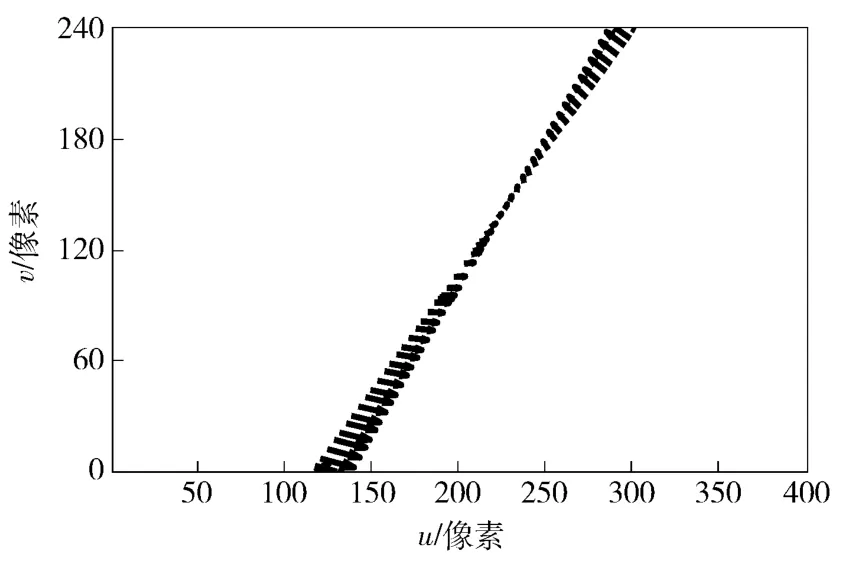
图6 直线稀疏光流场提取算法获得的稀疏光流场Fig.6 Sparse line-optical flow field calculated by the proposed method

由上述仿真结果可以看出，直线稀疏光流场与Horn 算法一样，都可以精确描述图像中边缘附近的运动情况。由于没有该序列图像的标准光流场，使用参考文献［15］中的光流场误差测量算法对该算法相对于Horn 算法的进行误差测量，从而评估该算法。使用本算法计算出的直线稀疏光流场与Horn算法计算出的全局光流场相比，取其边缘附近对应点的光流值，并按照(25)式计算各个点的角误差，

图7 采用Horn 算法计算的全局光流场Fig.7 Global optical flow field calculated by Horn algorithm

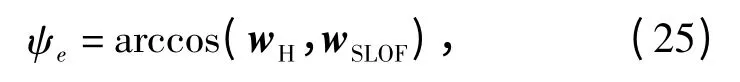
式中:wH为Horn 算法计算的光流矢量;wSLOF为本算法计算的光流矢量。

计算本算法得到光流场相对于Horn 算法得到的光流场的相对平均角误差(RAAE)和相对标准差(RSTD)，见表1.

表1 本算法相对于Horn 算法获取的光流场误差Tab.1 RAAE and RSTD errors of globe optical flow field calculated by the proposed method

从上述误差分析结果来看，使用直线稀疏光流场提取算法获取的光流场在图像边缘附近的精度与Horn 算法获得的较为接近，平均误差为4.733 9° ±2.875 2°，因此可以替代后者对图像中直线特征的边缘区域进行光流分析;同时，由于使用本方法的时间开销要远远小于Horn 算法，耗时仅相当于后者的6%，因此本算法更适合诸如无人飞行器视觉导航等对于算法实时性要求较高的场合应用。

3.2 基于直线稀疏光流场的姿态提取实验

为了验证直线稀疏光流场的姿态提取算法，使用无人机搭载摄像机进行航拍实验，同时利用机载导航设备记录姿态信息。机载导航设备使用ADIS16405 陀螺测量飞行器实时的角速度信息，其动态响应范围为±300°/s，采样率为100 Hz，三轴陀螺仪的角速度测量误差为±0.05°，加速度计量程±18 g，测量误差±9 mg. 航拍摄像机采用1/3 in 的CCD 摄像机，视场角是30°，摄像机有效像素1 024×768.

对航拍图像序列离线计算其直线稀疏光流场，估计飞行器的姿态信息，并与机载导航设备获取的姿态信息进行比较，验证算法的可行性。

首先对航拍图像进行地平线提取，提取算法采用Sobel 边缘提取复合旋转投影算法提取地平线［2］，在此不再赘述。部分帧地平线提取结果如图8所示。

图8 第36 帧和第37 帧地平线提取结果Fig.8 Horizons extracted in 36th frame and 37th frame

依据直线稀疏光流场提取算法，可得两帧之间的直线光流场如图8所示，用时0.328 7 s.

图9为使用本文方法获取的直线稀疏光流场。为了对比，同时使用Horn 算法计算两帧图像间的全局光流场，耗时4.713 s，光流场如图10所示。由上述仿真结果可以看出，使用直线稀疏光流场提取算法获取的图像地平线光流相较于使用Horn 方法计算而得到的全局光流，更不易受到诸如地面水体反射、空中云雾等噪声的影响，因此可以更准确地估计出图像中直线部分的光流信息，同时相比Horn 方法具有更快的计算速度。

图9 使用直线稀疏光流提取得到的稀疏光流场Fig.9 Sparse line-optical flow field calculated by the proposed method

获取图像的直线稀疏光流场后，利用(23)式即可完成飞行器俯仰角速度、滚转角速度和偏航角速度的解算。对100 帧航拍图像使用上述方法进行计算，并对比机载导航系统角速度陀螺的输出，如图11～图13所示。

图10 使用Horn 方法计算的图像全局光流场Fig.10 Global optical flow field calculated by Horn algorithm

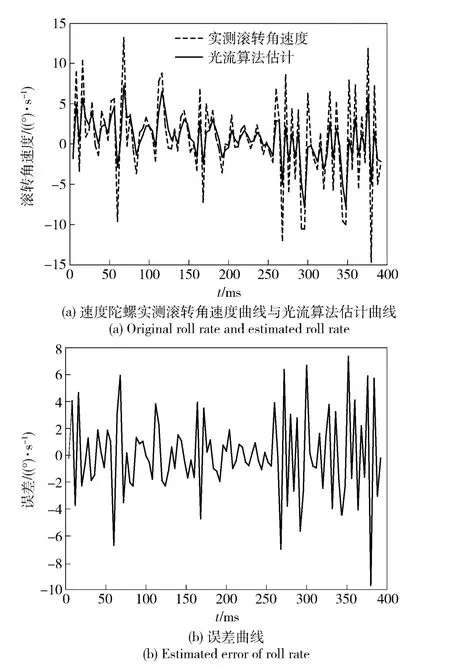
图11 使用稀疏光流场进行的滚转角速度估计及其估计误差曲线Fig.11 Roll rate and its errors estimated with sparse optical flow field

结合图11～图13可看出，使用稀疏光流场可以用来估计俯仰、偏航、滚转三通道的飞行器角速度信息，其最大估计误差除滚转通道小于±10°/s 外，其余两通道最大估计误差均小于±5°/s. 还可发现，稀疏光流场估计姿态角的精度与该通道的角速度正相关，在角速度比较小的情况下，使用稀疏光流场还是可以获得较高的估计精度，而当飞行器角速度增大时，估计误差随即增大。

造成这种估计误差较大的一个因素是图像信息的采样率要低于角速度陀螺的采样率，本飞行实验采用的陀螺采样率达到100 Hz，而使用航拍图像的图像帧率只有25 帧/s，由于光流估计的数据采样率不足，从而带来了一定的估计误差;另一个因素是本文中只使用了地平线一条直线计算其附近的稀疏光流场，带来了一定的估计误差，理论上在进行合理的直线匹配之后，本算法可以获取视场中多条典型直线特征附近的稀疏光流场，利用多条直线的稀疏光流场进行姿态角估计将提高本算法的估计精度。

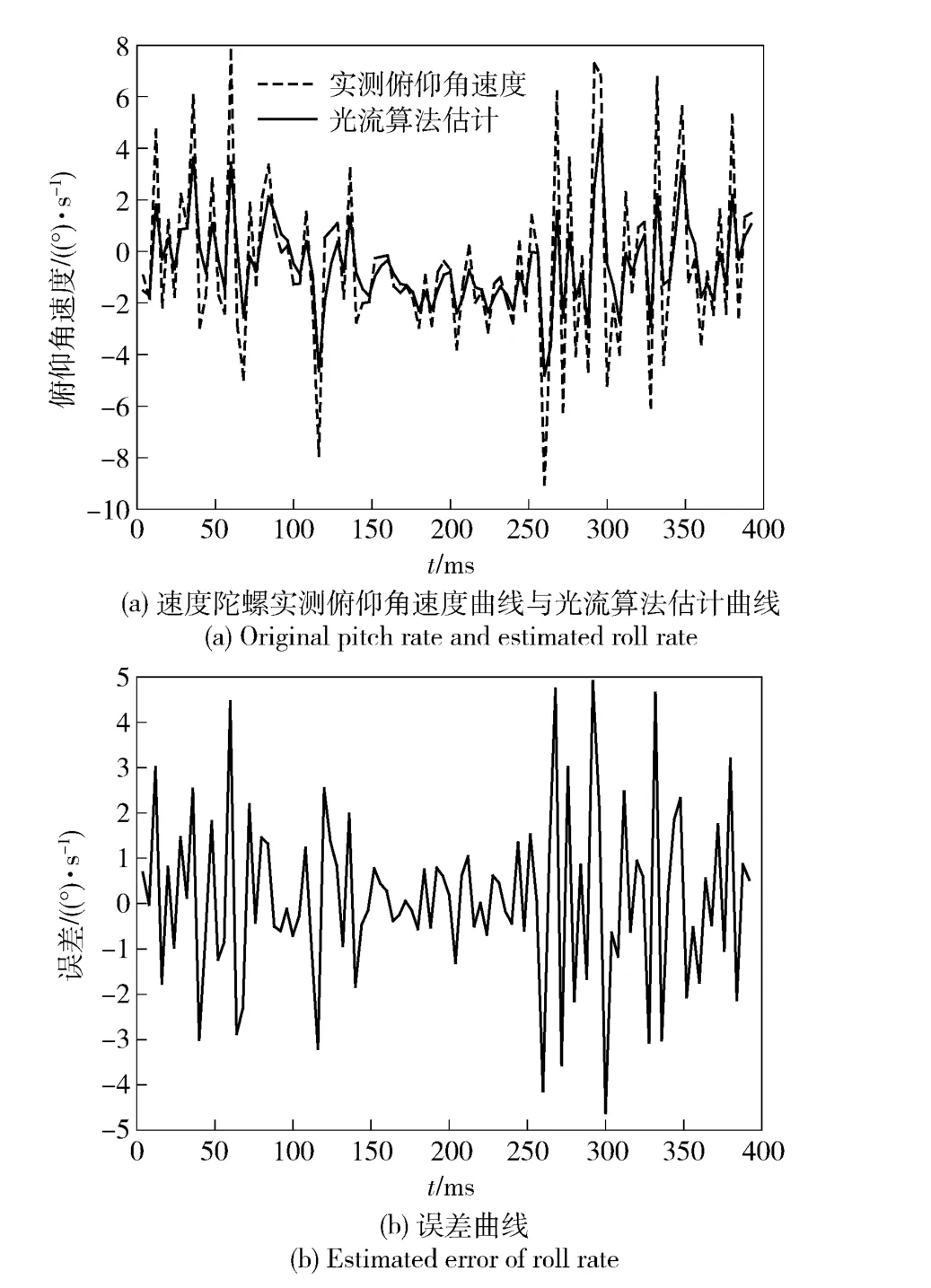
图12 使用稀疏光流场进行的俯仰角速度估计及其估计误差曲线Fig.12 Pitch rate and errors estimated with sparse optical flow field

4 总结

本文提出了一种基于直线的稀疏光流场计算方法，并进行了理论分析与仿真，确定了该方法在计算图像局部光流问题上的有效性;并提出了一种基于直线稀疏光流场的飞行器姿态角信息提取方法，是现有无人飞行器导航手段的有效替代和补充。通过该方法，可以实时提取飞行器的俯仰角速度、滚转角速度和偏航角速度信息。对实际飞行实验获得航拍数据进行仿真并对比同时采集的导航数据，结果显示，该算法在滚转通道角速度误差在±10°/s，在俯仰和偏航通道角速度估计误差均小于±5°/s.

需要指出的是，该方法不仅能够获得地平线附近的直线稀疏光流场，通过合理的直线匹配，该方法也可以计算出视场中存在的多条典型直线特征附近的稀疏光流场。使用上述多条直线的稀疏光流场来估计飞行器的姿态信息，将可以提高本算法的估计精度。

图13 使用稀疏光流场进行的偏航角速度估计及其估计误差曲线Fig.13 Yaw rate and its errors estimated with sparse optical flow field

References)

［1］ 蔡瑜，叶雄英，朱荣，等. 用于微小飞行器姿态测量的红外地平仪研制［J］. 仪表技术与传感器，2009 (7):33 -35.CAI Yu，YE Xiong-ying，ZHU Rong，et al. Infrared horizon detector making for measuring micro air vehicle attitude［J］. Instrument Technique and Sensor，2009(7):33 -35. (in Chinese)

［2］ Bao G Q，Xiong S S，Zhou Z Y. Vision-based horizon extraction for micro air vehicle flight control［J］. IEEE Transactions on Instrumentation and Measurement，2005，54(3):1067 -1072.

［3］ Pereira G A S，Iscold P，Torres L A B. Airplane attitude estimation using computer vision:simple method and actual experiments［J］.Electronics Letters，2008，44(22):1303 -1305.

［4］ Ettinger S M，Nechyba M C，Ifju P G，et al. Vision guided flight stability and control for micro air vehicles［J］. Advanced Robotics，2003，17(7):617 -640.

［5］ Todorovic S，Nechyba M C，Ifju P G. Sky/ground modeling for autonomous MAV flight［C］∥IEEE International Conference on Robotics and Automation. Taipei:IEEE，2003:1422 -1427.

［6］ Fefilatyev S，Smarodzinava V，Hall L O，et al. Horizon detection using machine learning techniques［C］∥Proceedings of 5th International Conference on Machine Learning and Applications. Orlando，US:IEEE，2006:17 -21.

［7］ Chiu C C，Lo C T. Vision-only automatic flight control for small uavs［J］. IEEE Transactions on Vehicular Technology，2011，60(6):2425 -2437.

［8］ Cornall T D，Egan G K，Price A. Aircraft attitude estimation from horizon video［J］. Electronics Letters，2006，42(13):744 -745.

［9］ Thurrowgood S，Moore R J D，Bland D，et al. UAV attitude control using the visual horizon［C］∥Proceedings of the 2010 Australasian Conference on Robotics and Automation. Brisbane，Australia:IRAA，2010.

［10］ Grzywna J W，Jain A，Plew J，et al. Rapid development of visionbased control for MAVs through a virtual flight testbed［C］∥IEEE International Conference on Robotics and Automation. Barcelona，Spain:IEEE，2005:3696 -3702.

［11］ 程序，郝群，宋勇，等. 基于直线模型的卫星飞行器姿态角计算［J］. 北京理工大学学报，2010，30(7):798 -802.CHENG Xu，HAO Qun，SONG Yong，et al.Method for calculating MAV attitude angles based on straight line model［J］. Transactions of Beijing Institute of Technology，2010，30(7):798 -802. (in Chinese)

［12］ Dusha D，Mejias L，Walker R. Fixed-wing attitude estimation using temporal tracking of the horizon and optical flow［J］. Journal of Field Robotics，2011，28(3):355 -372.

［13］ Shabayek A E R，Demonceaux C，Morel O，et al. Vision based UAV attitude estimation:progress and insights［J］. Journal of Intelligent ＆ Robotic Systems，2012，65(1/2/3/4):295 -308.

［14］ Horn B K，Schunck B G. Determining optical flow［J］.Artificial Intelligence，1981，17:185 -203.

［15］ Lucas B D，Kanade T. An iterative image registration technique with an application to stereo vision［C］∥Proceedings of 7th International Joint Conference on Artificial Intelligence. Vancouver. British Columbia，Canada:San Francico，CA:Morgan Kaufmann Pubishers Inc，1981:674 -679.

［16］ Terzopoulos D. Regularization of inverse visual problems involving discontinuities［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，1986，8(4):413 -424.

［17］ Hildreth E C. The measurement of visual motion［M］. Cambridge，Massachusetts:MIT Press，1984.

［18］ Barron J L，Fleet D J，Beauchemin S S. Performance of optical flow techniques［J］. International Journal of Computer Vision，1994，12(1):43 -77.