基于粗糙集理论的遗传属性约简算法研究

孙玲芳，许 锋，周家波，侯志鲁

(1.泰州学院数理信息学院，江苏泰州225300)(2.江苏科技大学经济管理学院，江苏镇江212003)(3.江苏科技大学计算机科学与工程学院，江苏镇江212003)

遗传算法是模拟自然界生物进化过程和机制求解问题的一类自适应和自组织的人工智能技术［1］.粗糙集理论［2］已在机器学习［3］、数据挖掘［4］和智能决策中取得成功应用.早在90年代学者们就利用遗传算法来求解信息系统的属性约简［5］.传统的属性约简遗传算法收敛速度慢，容易陷入局部极小值，存在早熟的问题，效率低下，难以适应实时性的应用［6］.2004年，文献［7］提出一种基于不完备信息表的属性约简算法，并在算法中首次提出了相似的概念，但是此算法效率低下也存在早熟的问题.文献［8］将属性核加入遗传算法的初始种群，增加收敛速度，引入决策属性对条件属性的依赖度提高了算法的收敛速度，但却容易陷入局部最优解.文献［9］设计了一种计算适应度函数的快速方法，提高了算法的速度，适应处理大型决策表，但还是不能满足实时检测的需求.

文中首先对适应度函数做了改进，减少了算法运算时间，提高了效率.其次对变异的方式和变异概率做了改进，保证算法不陷入局部最小值的同时控制了算法的进化方向.文献［10］提出了一种自适应遗传算法，文中也对选择概率做了改进，让选择概率动态调整，在算法初始阶段使用较大的选择概率，让大量的新个体进入算法，随着个体变化的减小，选择概率也随之减小，使大量的优秀个体保留下来，加快收敛速度.最后对修正算子也做了改进，为了加快算法收敛，使用启发性的修正算子.

1 相关理论和定理

粗糙集理论是处理含糊性和不确定性的一种数学工具.其核心就是关于知识、集合的划分及近似集等概念.它最重要的功能就是在浩瀚的数据中找到有用的知识.通常将知识系统表示为一张二维表.表中有很多属性包括条件属性和决策属性，有些属性对决策属性有影响，而有些没有.根据粗糙集理论将无影响的条件属性去掉就叫属性约简.

定义1［9］令决策表定义为 S=(U，C，D，V，f，d)，其中U=(x1，x2，x3，…，xR)是论域;C={c1，c2，…，cr}为条件属性集;D为决策属性集;f:U×C→V和d:U×D→V是信息函数，其中F=C∪D，C∩D= φ，V=∪Va，a∈F，Va表示属性a的值域.

定义 2 决策表 S=(U，C，D，V，f，d)中，∀R⊆C，X⊆U，记U/R={R1，R2，…，Rl}，则称=∪为X关于R的下近似集.称RX=∪{Ri|Ri∈U/R，Ri∩X≠φ}.集合bnR(X)=称作x的R边界域是根据知识R判断肯定属于X的U中元素中组成的集合是根据那些知识R判断可能属于X的U中元素组成的集合［9］.

定义3［11］在一个决策表S=(U，C，D，V，f，d)中，设U/D={D1，D2，…，Dk}表示由决策属性集 D对论域 U 的划分，U/C={C1，C2，…，Cm}表示由条件属性集C对论域U的划分，称C-(Di)为C关于D的正区域.计算POSC(D)的时间复杂度为 O(|C||U|2)［12］.

定义4 设W⊆U对于分类U/a，定义W的下近似为W(U/a)-用Sa(W)来表示.子集Sa(W)称为W关于属性a的支持子集.spta(W)=|Sa(W)|/|U|称为W关于属性a的支持度.

定义5 设y∈D是决策表(U，A)中一个决策属性，A=C∪D，C∩D=φ.决策属性y∈D关于条件属性a∈C的支持子集为Sa(y)，V⊆WV)，spta(y)=|Sa(y)|/|U|称为y关于a的支持度.

定义6 设W⊆U是u的子集，考虑W关于条件属性集的支持度.对于决策表(U，C∪D)中的条件属性集X⊆C，W关于X的支持子集是SX(W)=，V⊆WV称为W关于X的支持度.

定义7 在决策表中，X1→X2(Y)成立当且仅当SX1(Y)⊇ SX2(Y)，即对于每个 W⊆ U/Y，有SX1(W)⊇ SX2(W).知道如果 X1⊇ X2，则 X1→X2(Y).X1→X2(Y)意味着规则“X1蕴涵Y”比规则“X2蕴涵Y”更强.

定义8 令(U，A)是一个决策表，A=C∪D，C∩D=φ.其中c是条件属性集，D是决策属性集.两个属性子集X1，X2⊆C之间的恒等依赖(对于决策属性子集Y⊆D而言)是一个描述，用X1→X2(Y)来表示.在决策表中，X1↔X2(Y)成立的充要条件是SX1(Y)=SX2(Y);即对于每个W⊆U/Y，有SX1(W)=SX2(W).

定义9 令(U，A)是一个决策表，A=C∪D，C∩D=φ.其中C是条件属性集，D是决策属性集.X1⊇X2蕴涵SX1(Y)⊇SX2(Y)因此有如下定理:①SC(Y)⊇SX(Y)即对于所有的X⊆C，Y⊆D，有C→X(Y).② SX1(Y)⊇SX-{x}(Y)即对于非空集X⊆C，x∈X和Y⊆D，有X→(X-{x})(Y).令φ⊂X⊆C，φ⊂Y⊆D，U/Y≠U/δ={U}.给定x∈X，如果SX(Y)⊇SX-{x}(Y)，则称x在X中时重要的(对于Y而言的);如果，则称x在X中不重要(对于Y而言的).

定义10 令φ⊂X⊆C，φ⊂Y⊆D，U/Y≠U/δ={U}.所有在X中是重要的属性x∈X组成的集合(对于Y而言的)称为X的核(对于Y而言的)，用CYX来表示，即中定义

定义11 令(U，A)是一个决策表，A=C∪D，C∩D=φ.其中C是条件属性集，D是决策属性集.令φ⊂X⊆C，φ⊂Y⊆D，U/Y≠U/δ={U}.如果每个x∈X在X中是重要的(对于Y而言的)，则称非空子集X是独立的(对于Y而言的);否则X是依赖的(对于Y而言的).空集φ称为独立的(对于Y而言的).

定义12 令(U，A)是一个决策表，A=C∪D，C∩D=φ.其中C是条件属性集，D是决策属性集.令φ⊂X⊆C，φ⊂Y⊆D，U/Y≠U/δ={U}.如果X0⊆X满足①SX0(Y)=SX(Y)，即X0↔X(Y).②如果 X·⊂X0则SX(Y)⊃SX·(Y)，即如果X·⊂X0则X·↔X(Y)不成立.则称X0是X的一个约简(对于Y而言的)［11］.

2 属性约简遗传算法的改进

2.1 属性的编码方法与初始种群的构建

遗传算法中有许多种编码方式，常用的有二进制编码、实数编码和符号编码等.每种编码方式各有优缺点.文中选用符号编码方式.该编码方式便于利用求解问题的专门知识，以及相关近似算法之间的混合使用.

染色体的长度视知识库中属性个数而定.每条染色体对应一个个体，每个基因位对应一个属性.基因位使用无数值含义的“0”和“1”来表示，“1”表示此个体中包涵基因位对应的属性，“0”表示此个体中不包含该基因位对应的属性.比如一个决策表有5个条件属性{a1，a2，a3，a4，a5}，一个可能的约简是{a1，a3，a4，a5}，则编码为“10101”.

在编码时，使用属性核限制初始种群对应基因位.根据粗糙集理论，属性核就是所有属性约简的交集，每个属性约简一定包涵了所有的核属性.为了减少个体产生的盲目性，使算法快速收敛，利用这一特性，对种群中所有个体的核基因位初始值设置为“1”，并且在以后交叉变异等一系列操作时不改变核基因位的值.核属性之外的属性值由计算机随机产生.

2.2 适应度函数的设计与算法结束的条件

在遗传算法中，适应度函数是整个算法的核心，它的设计关系到算法的收敛速度.遗传算法是以适应度函数作为目标函数，自适应地逼近目标值，渐进式优化，全局最优处理［13］.

由粗糙集理论得知，适应度函数的设置应体现两大思想.首先要保持约简后属性集合的分类能力(属性分类能力的计算粗糙集理论中已给出)，其次是保证约简后属性集所包涵的属性个数最少.简而言之，染色体中值为“1”的基因越少，则该染色体被选择的概率约大;染色体中所包含的属性分类能力越强，则被选择的概率越大.适应度函数在满足以上两种条件的同时还要兼顾到函数的复杂度，即函数计算的时间复杂度越低，遗传算法的效率越高，收敛速度越快.

鉴于以上考虑，适应度函数设计为

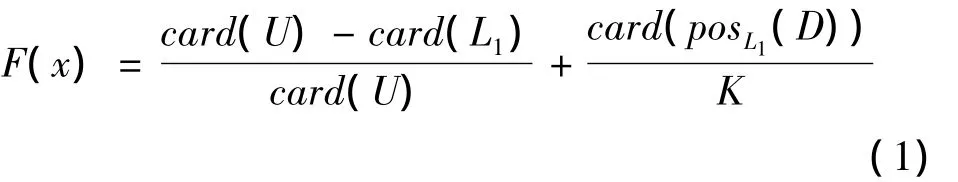
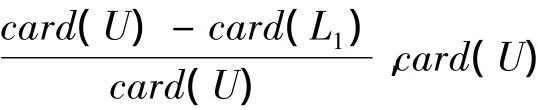
该函数由两部分组成:第一部分h(x)=表示信息系统U中所有属性的总和，card(L1)表示染色体L基因位值为“1”的属性的个数，即染色体中有用属性数.card(U)是一定的，当染色体中有用属性越少时，h(x)就越大，该个体被选择的概率就越大.

2.3 选择操作

在遗传算法中，选择算子是对个体进行优胜劣汰操作［14］，选择的方式和选择的概率对算法的结果有着重要的影响.

文中采用轮盘赌的方式进行选择［15］.设t为已经进化的代数，n为种群中个体的数量，best(t)表示前t代中最优个体，即适应度函数最大值对应的个体，bestF(t)是其适应度函数值.第t代第i个个体对应的适应度函数值为Fi(t)，则第i体的选择概率为

选择概率越大则被选择进入下一代的可能性越大.为了加快算法的收敛速度，利用轮盘赌方法产生子代个体后还要对个体修正，如果子代最优个体的适应度函数值小于bestF(t)，则将best(t)代替子代中适应度函数值最小的个体，反之则不操作.

2.4 交叉与种群修复操作

交叉采用单点交叉，先有计算机随机将种群里的个体两两配对，然后随机选择交叉点，以概率为Pcross进行交叉操作，Pcross一般在0.4～0.9之间.

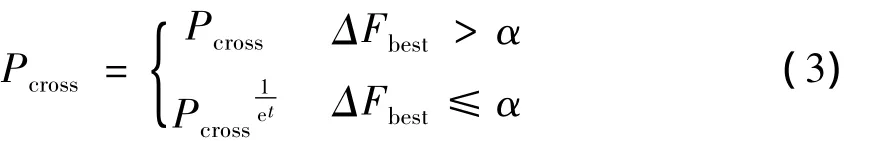
t为遗传的代数，ΔFbest为相邻代最优个体的适应度函数的差值，即ΔFbest=|Fmax(t-2)-Fmax(t-1)|Fbest(t)为第t代进化后在选择修正操作之前的最优个体的适应度函数值.规定第0代和第1代ΔFbest=0，选择是将个体中优秀的基因保留下来，当ΔFbest较大时，也就是在遗传算法运行的初期，需要保持种群的多样性，故采用较大的交叉概率;当ΔFbest趋于0时，也就是遗传算法后期，为了避免过大的交叉率对优良种群的破坏，故选择较小的交叉率.

为了确保算法的快速收敛，根据粗糙集理论，采用基因的重要度为启发信息对种群修复.当染色体posL1(D)=posU(D)时，说明L染色体中的属性具备了U中属性的分类能力，为了使L向最少有用属性方向进化，首先计算L中所有有用属性的重要性，将重要性最小的属性值由“1”变为“0”，若posL1(D)≠posU(D)时，可以认为，L染色体还没有优先满足分类能力的要求，则计算L中所有无用基因的重要性，选择重要性最大的属性，将其值由“0”变为“1”.

2.5 变异方式及概率设置

根据粗糙集理论将属性的重要性作为启发式信息，通过变异概率Pchange(t)反转某位等位基因的字符值来实现.为了保证算法的快速收敛，属性核对应的基因位不发生变异.给定一个染色体L=(a1，a2，a3，…，am)，变异后新个体为 L′=(a1′，a2′，a3′，…，am′)，设属性ai的值也用ai来表示，此时ai为数值型，则

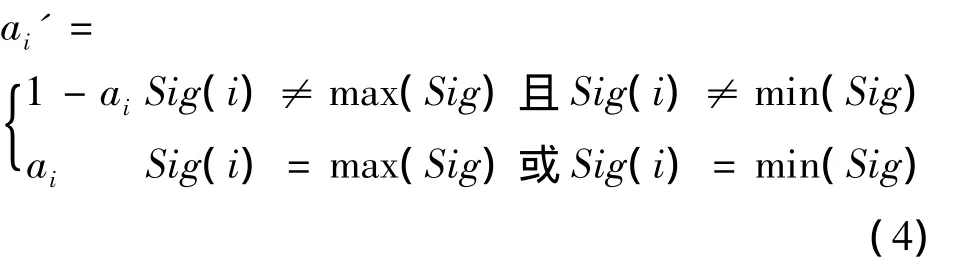
Sig(i)为个体中第i个属性的重要度，max(Sig)和min(Sig)分别表示个体中属性重要度的最大值和最小值.显然与传统的变异相比，同样只进行一次变异，本启发式变异算子将使群体保持更好的多样性.使用自适应变异概率，Pchange(t)设置为Pchange(t)=p+∂×(Nbest-1)，p表示基本变异概率，通常取0.03，Nbest表示连续出现当前最佳个体的适应度函数值不大于bestF(t)的次数.∂是调整因子，通常取较小的值.如果每次进化都有更优解出现，则Pchange(t)=p，变异概率较低，它表示算法在快速收敛，方向正确，不需要变异过多干预算法，通过选择交叉以及修复种群就能完成算法的快速收敛.当算法进入进化后期，个体趋于稳定，为了使算法不陷入局部最优解，Nbest变大使得Pchange(t)变大，扩大搜索范围.∂也是一个罚值，当，则代进化没有变化，认为算法陷入了早熟，就必须执行变异操作，使算法跳出早熟.可以证明，经过有限次操作定能跳出早熟.本算法通过连续几次变异而不是一次很大的变异跳出早熟，因而不至于过多的破坏当前进化成果.

3 属性约简遗传算法流程

算法:IARGA(S)

输入:S=(U，C，D，V，f)

输出:属性约简RLeast

1)输入 S=(U，C，D，V，f);

2)输入计算出S的核属性Rcore

3)输入种群的最大进化代数Tmax，初始化适应度函数值不发生变化罚值M，种群大小n，best=0，Fi(0)=0(i=1，2，3，4，…，n)RLeast= φ，种群矩阵a(n，m)=0，个体重要度矩阵b(n，m)best(t)= φ，bestF(t)=0，属性约简遗传算法流程如图1.

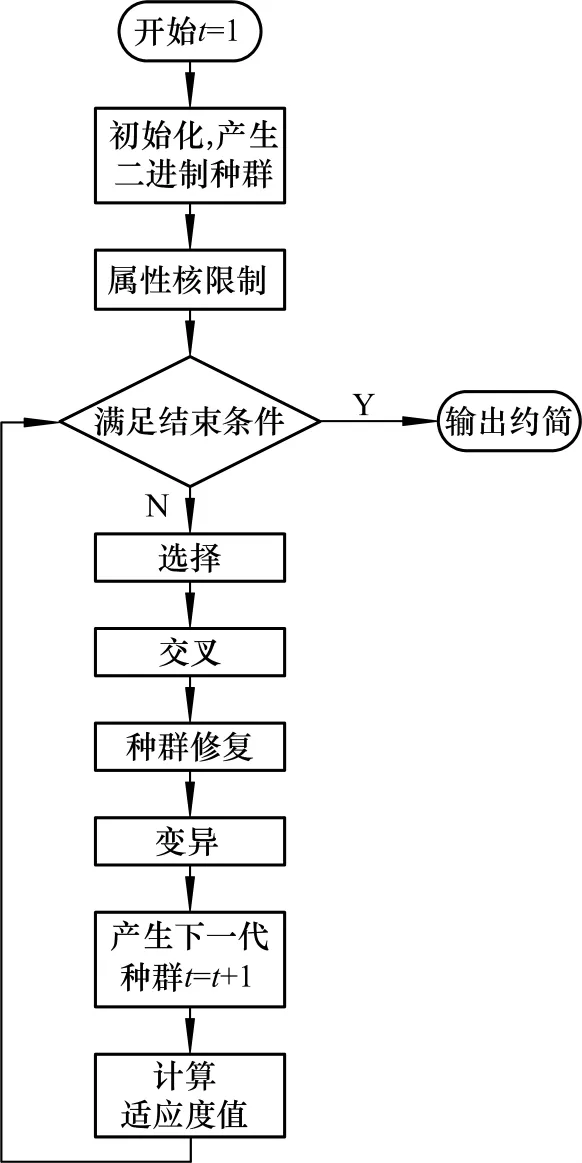
图1 属性约简遗传算法流程Fig.1 Flow diagram of IARGA(S)

4)对照Rcore，将种群矩阵a(n，m)中所有的核属性赋值“1”，其它属性随机赋值“0”或者“1”.

5)执行以下循环体:

for(t=0;t＜Tmax或者best＜M;t++)

{

①选择操作

计算每个个体的选择概率

以轮盘赌方法产生新种群a(n，m)，查询a(n，m)中适应度函数最大值Fmax(t)和最小值Fmin(t)，即对应的个体amax(t)和amin(t).

if Fmax(t)＜bestF(t)

then amin(t)=best(t);Fmax(t)=bestF(t);

②交叉操作

计算交叉概率Pcross

将种群中的个体随机两两配对

if rand1＜Pcross

then交换该对个体第j个基因位的值

};

③种群修复

计算种群中各个体中所有属性的重要性;将第j个体中第i个属性的重要性Sigj(i)保存至b(j，i);

then将L0中重要性最高的属性值设为“1”;

else将L1中重要性最低的属性值设为“0”;}

更新 a(n，m);

④变异操作

计算变异概率Pchange(t)=p+∂×(Nbest-1);

if rand2＜Pchange(t)

then for(i=1;i≤m;i++)

{if Sig(i)≠max(Sig)且Sig(i)≠min(Sig)then a(j，i)=1-a(j，i);

};

⑤产生下一代种群

计算每个个体的适应度函数值

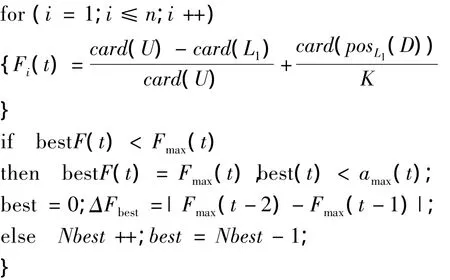
6)输出约简后的属性

ubest=best(t);

输出 ubest，输出 RLeast.

4 实验分析与性能比较

文中所述的算法与文献［9］中所述的算法是同一个主体，所以与文献［9］中的算法作对比.为了便于比对，本实验采用文献［9］的数据，种群大小为30［16］，对3个属性约简算法进行测试.实验环境为酷睿T2400双核处理器，主频为1.6 GHz，512 M内存，Windows XP操作系统.利用Matlab7.0工具编程实现算法.所谓大型知识系统是指数据的记录较多，一般达几万条，属性多而复杂的数据表.比如一般用于入侵检测实验的kddcup99数据集是贝尔实验室在美国空军网上采集的9个星期的网络连接数据，约60万条.每个数据都有41个特征属性，这样庞大的数据集就是大型知识系统.为了比对，突出算法本身的优越性，没有必要使用大型知识系统，所以选用了文献［9］使用的数据集.实验环境的配置也相对较低.实验数据如图2.

图2 决策表数据Fig.2 Diagram of decision table

属性1～9为条件属性，属性10为决策属性.由实验数据得知，利用本算法在Matlab上运行，算法循环12次收敛，第5次出现最优个体为(100110100)，其中和属性为(100110000)，这个结果与文献［9］中的结果一致.本算法用时523 ms与文献［9］比较节省较多的时间.比对结果如表1.

表1 常规遗传算法、文献［9］遗传算法与IARGA算法结果对照表Table 1 Contrast table of results from SGA GA in the ninth paper and LARGA

5 结论

从算法的整体设计入手，针对传统遗传算法对其适应度函数、交叉和变异的概率、变异方式和种群修复方式进行了全面的改进.基于粗糙集理论，利用属性重要性作为启发式信息，对种群修复方式和变异方式做了改进性设计，采用自适应的交叉和变异概率使算法收敛速度进一步提高.实验表明，IARGA算法克服了传统的遗传属性约简算法易于陷入局部极小值及效率低下的缺点，能有效地提高属性约简的效率.

References)

［1］ 朱果平.遗传算法在粗糙集属性约简中的研究［J］.太原科技，2010(3):83-84.Zhu Guoping.Research on genetic algorithm in attribute reduction of rough set［J］.Taiyuan Science and Technology，2010(3):83-84.(in Chinese)

［2］ Hewwitt J A.Technical services in 1983［J］.Library Resource Services，1984，28(3):205-218.

［3］ Pawlak Z，Grzymala-Busse J，Slowinski R.Rough sets［J］.Communications of the ACM，1995，8(11):89-95.

［4］ Swiniarski R W，Skowron A.Rough set methods in feature selection and recognition［J］.Pattern Recognition Lett，2003，24:833-849.

［5］ Liu H，Motoda H.Feature selection for knowledge discovery and data mining［D］.Boston:［s.n.］，1998.

［6］ Wroblewski J.Fing minimal reducts using genetic algorithms［A］∥In:Proc.2nd Annual Joint Conf.on Information Sciences.Wrightsville Beach，NC，September 28-October186-189，1995.

［7］ 郑志军，郑守淇.进化神经网络中的变异算子研究［J］. 软件学报，2002，13(4):726-731.Zheng Zhijun，Zheng Shouqi.Study on a mutation operator in evolving neural networks［J］.Journal of Software，2002，13(4):726-731.(in Chinese)

［8 ］ Leung Yee，Wu Weizhi，Zhang Wenxiu.Knowledge acquisition in incomplete information systems:A rough set approach ［J］.European Journal of Operational Research，2006，168:164-180.

［9］ 鲁霜.基于遗传算法的属性约简新方法［J］.现代计算机，2011(16):7-9，26.Lu Shuang.Research on maxiumum-matching algorithm of Chinese Word Segmentation arithmetic［J］.Modem Computer，2011(16):7-9，26.(in Chinese)

［10］ 杨波，徐章艳，舒文豪.一种快速的Rough集属性约简遗传算法［J］.小型微型计算机系统，2012，33(1):140-144.Yang Bo，Xu Zhangyan，Shu Wenhao.Efficient genetic algorithm of attribute reduction based on rough set［J］.Mimi-micro Systems，2012，33(1):140-144.(in Chinese)

［11］ Srinvas M，Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm［J］.IEEE Trans on Systems，Man and Cybernetics，1994，24(4):162-167.

［12］ 张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京:科学出版社，2001:1-222.

［13］ Miao D Q，Wang J.An information-based algorithm for reduction of knowledge［J］.IEEE International Conference on Interlligent Processing Systems，1997，28(2):28-31.

［14］ 邹瑞芝.一种基于遗传算法的粗糙集属性约简算法［J］.电脑知识与技术，2011，7(12):2943-2944.

［15］ Tao Zhi，Liu Qingzheng，Li Weimin.Attribute reduction based on GA under incomplete information system［J］.Systems Engineering and Electronics，2007，29(9):1484-1487.

［16］ 孙娓娓，王春生，姚云飞.基于自适应遗传算法的粗糙集属性约简算法［J］.计算机工程与应用，2011，47(33):49-51.Sun Weiwei，Wang Chunsheng，Yao Yunfei.Rough set attribute reduction algorithm based on adaptive genetic algorithm［J］.Computer Engineering and Applications，2011，47(33):49-51.(in Chinese)

［17］ 刘晓霞，窦明鑫.种群规模对遗传算法性能的影响［J］. 合作经济与科技，2012，4(438):116-117.