基于模糊层次分析法的水资源承载力研究

王海亮，杨永红，张颖

（1.西藏大学农牧学院，西藏林芝 860000；2.河北省水利水电勘测设计研究院，天津 300250）

基于模糊层次分析法的水资源承载力研究

王海亮1，杨永红1，张颖2

（1.西藏大学农牧学院，西藏林芝 860000；2.河北省水利水电勘测设计研究院，天津 300250）

针对林芝地区水资源的实际情况，建立了水资源承载力层次结构模型，准则层分为5个指标，因素层选择了15个指标，进行了林芝地区水资源承载力的评价，在评价过程中，把层次分析法（AHP法）和模糊评价两种数学方法相结合，分别建立了数学模型，运用Matlab进行编程，得出模糊评价的最终得分，说明水资源承载力满足要求并处于良好状态。

层次分析法；模糊评价；水资源承载力；林芝地区

水资源承载力是一个地区乃至一个国家持续发展过程中自然资源承载力重要组成部分，也是水资源紧缺和干旱地区制约人类社会发展的关键因素［1-2］。

水资源承载力研究是一项集评价、规划以及预测一体化的综合课题，其研究目的是使人口、资源、环境和经济相协调［3-4］。我国多数城市发展受到水资源短缺的制约，因此，研究水资源承载力，对该区域的水资源优化配置、生态环境建设、人民生活水平的提升、工农业的快速发展、实现区域可持续发展有着重要的理论和现实意义。

西藏正在经历跨越式发展，林芝作为西藏区域内经济水平最为发达的地区，人均工业产值仅2000元，这与区外经济发达地区的人均工业产值相差巨大［5］。近年来，该地区的经济发展速度明显加快，水污染逐年严重，水资源的消耗也在逐年增加，因此，在经济快速发展的情况下，开展水资源承载力的研究已刻不容缓。

水资源承载力评估方法主要有层次分析法和模糊评价法，层次分析法和模糊评价法都有其局限性，所以，将两种方法相结合，对林芝地区水资源承载力进行评价。

1 林芝地区水资源及其利用概况

林芝地区水资源在西藏的占有量超过70%，年平均降水660.1mm［6］，5～9月份为主要降雨时间，降水充沛，超过了全年降水量的82%。本地区的河流主要属于雅江和怒江两大水系，雅江全长2057km，年径流量1380亿m3，平均流量4425m3/s，在林芝地区的主要支流有尼洋河、帕隆藏布等，尼洋河流经工布江达和林芝两个县，长315km，年径流量220亿m3，平均流量584m3/s；帕隆藏布为雅江下游一条支流，在雅江支流中水量最大，平均流量1009m3/s。怒江流径林芝地区东部，长140km，平均流量584m3/s。

目前，林芝地区水资源利用主要有农业、生活、工业和林牧渔畜等用水类型，其中由于林芝地区人口数量相对较少，工业发展相对落后，所以主要消耗水资源的为农业用水，具体水资源利用情况还需精细计算［5］。

2 模型指标体系的构建

水资源承载力的指标能够判断水资源承载力的大小，但是由于水资源承载力的评价涉及内容广，如何通过水资源承载力的内涵来实现水资源的可持续利用，从众多复杂的因素中选择与预测评价目标及当地实际情况相符，并能够具有一定可操作性的指标体系，是水资源承载力预测评价的关键。

水资源承载力研究的大系统主要包括资源环境、社会经济和人口。这个系统既包括自然因素的影响，又包括社会经济等因素的影响。因为系统内影响因素纷繁复杂，在建立层次结构模型时，最好选择具有代表性的对水资源承载力影响比较大的一些指标［7-13］。根据林芝地区水资源及流域特征，将水资源承载力作为目标层，将水资源质量、水资源数量、水资源利用、用水水平和社会经济5个指标作为准则层，准则层下设15个因素作为因素层，层次结构如图1。

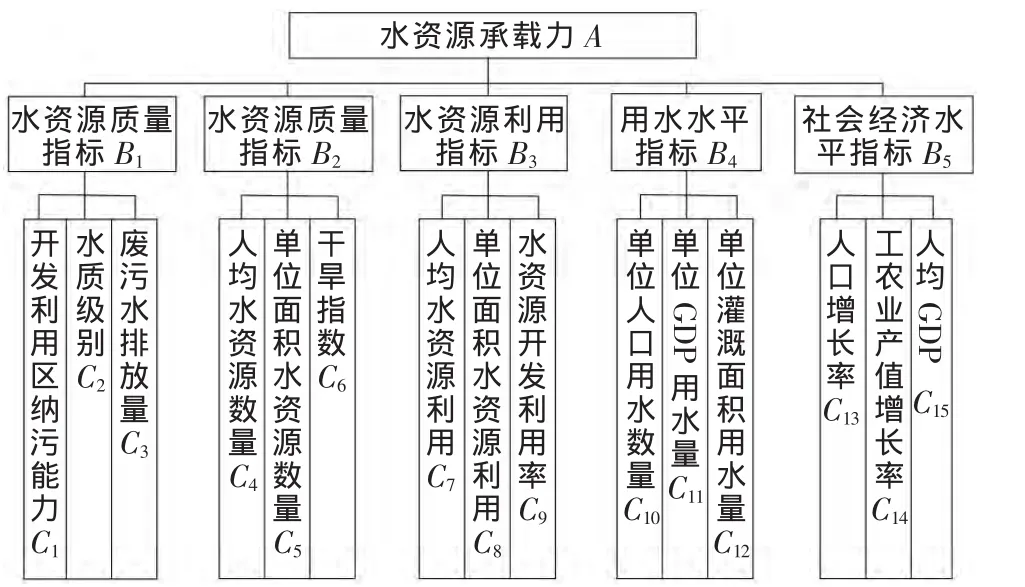
图1 水资源承载力模型指标体系

3 模型构建及基本原理

水资源承载力评价模型采用层次分析法和模糊评价法联合构建。

层次分析法［14-16］是一种能够有效确定权重系数的方法，他把各种问题中纷繁复杂的因素划分为层次清晰明显的有序层。

模糊评价法［17-20］是一种能将综合评价作出量化的数学方法，主要针对受多因素影响的模糊现象［21-22］。现在将两者相结合，对林芝地区水资源承载力进行评价。该方法用层次分析法确定评价体系中各指标的权重，然后根据客观情况进行模糊评判，最后得出终值［23-24］。

3.1 AHP法确定指标权重

3.1.1 构造判断矩阵

在层次结构模型中，层次结构体现了各个因素之间的关系，权重是同一层次的指标影响上一个层次指标的重要程度，这个层次中指标的个数即为判断矩阵的维数，例如，构造判断矩阵A，B1，B2，B3，B4。Bi（i=1，2，3，4）的个数就为此矩阵的维数。所得矩阵如表1，其他矩阵同理。

这里aij的确定用1～9比例标度对其赋值，判断矩阵标度如表2。

表1 判断矩阵

表2 判断矩阵标度

3.1.2 计算各判断矩阵的最大特征值、特征向量并判断一致性

在计算判断矩阵最大特征值、特征向量并判断一致性［25-31］时，主要依托于Matlab编程［32］，其数学模型为：

判断矩阵满足一致性要求的依据为随机一次性比率CR（CR=CI/RI），当CR<0.1时，判断矩阵满足一致性，反之，需要构造新的判断矩阵重新进行判断。RI为平均随机一次性指标，其值可查表3。

表3 平均随机一致性指标

3.2 模糊评价法确定总得分

3.2.1 确定指标集合和评语集合

由建立的层次结构模型可以确定评价指标的集合，若层次结构模型分为n层，则评价指标分为（n-1）个层次，根据AHP进行分析，得到指标权重；本文评语集合采用的是4级，即V=［V1，V2，V3，V4］；分别代表了优、良、一般、差4个级别，为了更加准确地反映当地水资源承载力情况，进一步将评语级别赋予其值，如表4。

表4 评价等级对应的取值

3.2.2 确定总得分

模糊评价部分同样是建立数学模型，通过Matlab编程获得评价结果，及模糊评价的总得分。

模糊评价所建立的数学模型如下：

式中S为模糊评价的总得分；A为系统评价矩阵；FT为相应因素的得分；W为各因素对应的权重；B为总评价矩阵；Wi为各因素对应子因素的权重，由子因素的影响大小决定；Ri为各因素对应的评价矩阵。

在求子评价矩阵Bi和系统评价矩阵A时，应该注意归一化处理。

4 评价实例

根据林芝地区的客观实际，层次结构模型中准则层选取了5个指标，即水资源质量指标、水资源数量指标、水资源利用指标、用水水平指标和社会经济水平指标。在因素层选取了15个相关因素，由以上各指标因素构造的判断矩阵如表5～表10。

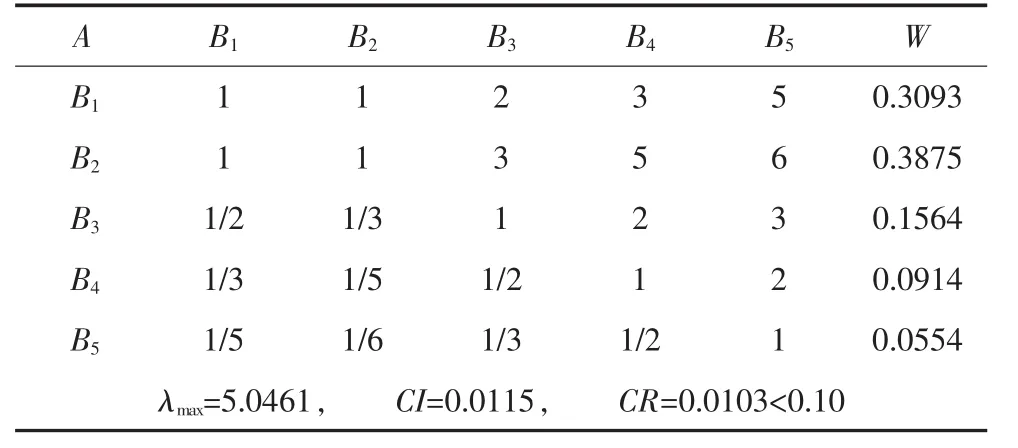
表5 准则层B对目标层A的判断矩阵

表6 因素层对准则层B1的判断矩阵

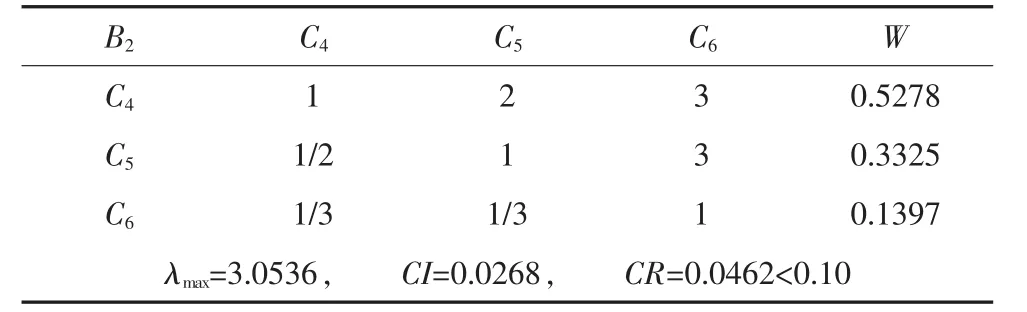
表7 因素层对准则层B2的判断矩阵

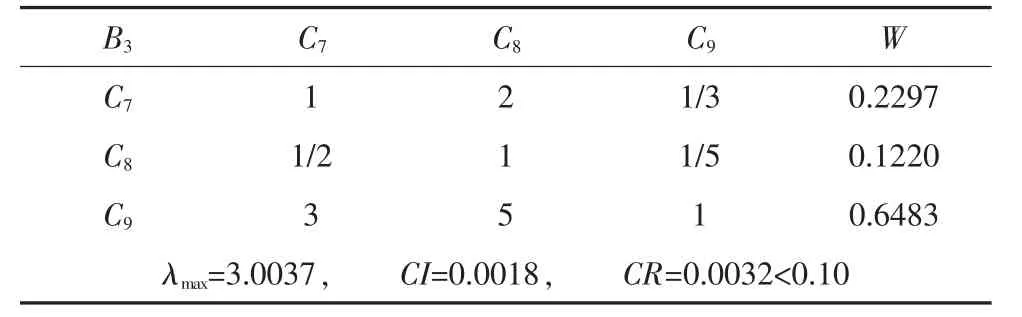
表8 因素层对准则层B3的判断矩阵

表9 因素层对准则层B4的判断矩阵

表10 因素层对准则层B5的判断矩阵

经过一致性计算可知，所有判断矩阵的一致性满足要求，各个矩阵都为有效判断矩阵及权重值满足要求。

方案所对应各个指标的模糊评价如表11所示。

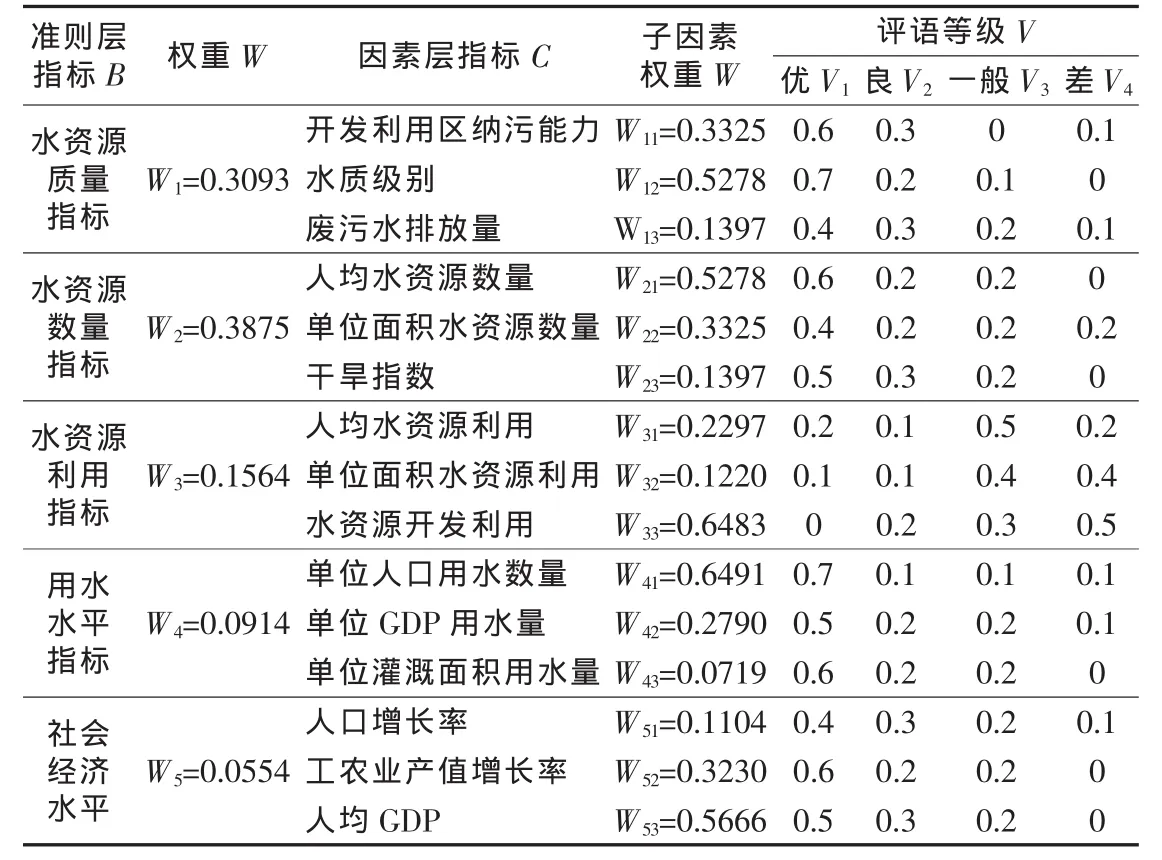
表11 水资源承载力指标等级评分

根据模糊评价的数学模型中式（3）及表中数据，可以得到因素层指标所对应的评价矩阵，即方案对于准则层各个指标B的模糊评语Bi（i=1，2，3，4，5），结果如下：

由数学模型中式（6）和模糊评语Bi可以计算出系统评价矩阵，即总的模糊评语：

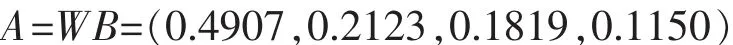
其中，B=（B1，B2，B3，B4，B5）

最后确定一个权数FT=（100，80，60，40），计算模糊评价的最终总得分S=AFT=0.4907×100+0.2123× 80+0.1819×60+0.1150×40=81.5680。

5 结语

（1）通过西藏林芝地区水资源及其利用状况，建立了水资源承载力层次结构模型，确定了各项指标与因素，模型直观，层次清晰。

（2）通过AHP与模糊评价相结合的方法确定最后的评价总得分为81.5680，说明林芝地区当前水资源承载力满足要求并处于良好状态。

［1］汤奇成，张捷斌.西北干旱地区水资源与生态环境保护［J］.地理科学进展，2001（3）:226-232.

［2］朱一中，夏军，谈戈.关于水资源承载力理论与方法的研究［J］.地理科学进展，2002（2）:180-188.

［3］惠泱河，蒋晓辉，黄强，等.二元模式下水资源承载力系统动态仿真模型研究［J］.地理研究，2001（2）:191-198.

［4］张兰.区域水资源承载力研究及其应用［D］.南京：河海大学，2006.

［5］宗永臣，拉姆次仁，金建立.西藏林芝地区水资源承载力研究［J］.南水北调与水利科技，2012（5）:37-42.［6］李朝霞，熊义东.西藏林芝地区水资源可持续开发利用研究［J］.西藏科技，2005（1）:18-20.

［7］张郁，陈玉洁.山东省水资源承载力分析［J］.滨州学院学报，2013（3）:114-120.

［8］许有鹏.干旱区水资源承载能力综合评价研究——以新疆和田河流域为例［J］.自然资源学报，1993（3）: 229-237.

［9］文琦，何彤慧.近10年来我国水资源承载力研究综述［J］.水资源保护，2005（6）:19-22.

［10］刘树锋，陈俊合.基于神经网络理论的水资源承载力研究［J］.资源科学，2007（1）:99-105.

［11］惠泱河，蒋晓辉，黄强，等.二元模式下水资源承载力系统动态仿真模型研究［J］.地理研究，2001（2）:191-198.

［12］侯志华.水资源承载力研究进展［J］.资源开发与市场，2008（3）:248-251.

［13］傅湘，纪昌明.区域水资源承载能力综合评价──主成分分析法的应用［J］.长江流域资源与环境，1999（2）:168-173.

［14］张祥娟，李新，李秀霞，等.用层次分析法建立京杭大运河苏州高新区段水环境承载力指标体系研究［J］.环境保护与循环经济，2011（2）:42-44，49.

［15］胡国祥，聂国平，伍振志.层次分析法在工程评标中的应用［J］.安徽建筑，2003（4）:110-112.

［16］董艳.层次分析法在合理选择网络攻击时间中的应用［D］.成都：电子科技大学，2005.

［17］薛永森.县级农村公路现状适应性的模糊评价［D］.南京：南京农业大学，2006.

［18］付二晴，蔡建峰.基于能力知识管理水平的模糊评价［J］.情报科学，2006（5）:663-667.

［19］王小群，张兴容.模糊评价数学模型在企业安全评价中的应用［J］.工业安全与环保，2002（12）:29-32.

［20］于声.模糊评价法在区域工业用地适宜性评价中应用［D］.北京：中国农业科学院，2007.

［21］郭金玉，张忠彬，孙庆云.层次分析法在安全科学研究中的应用［J］.中国安全生产科学技术，2008（2）:69-73.

［22］刘铁民，张兴凯，刘功智.安全评价方法应用指南［M］.北京:化学工业出版社，2005.

［23］唐中富，姚泽华，钱剑雄，等.基于模糊评价和层次分析法的客运索道安全评价方法研究［J］.中国安全科学学报，2008（6）:152-157.

［24］李嘉，张翊.AHP和模糊评价法相结合的公路网规划方案评价研究［J］.中南公路工程，2006（2）:51-53，72.

［25］王国华，梁樑.专家判断矩阵的一种调整方法［J］.系统工程，2001（4）:90-96.

［26］刘万里，雷治军.关于AHP中判断矩阵校正方法的研究［J］.系统工程理论与实践，1997（6）:31-35，40.

［27］徐泽水.判断矩阵一致性修正的新方法［J］.系统工程理论与实践，2000（4）:86-89.

［28］李梅霞.AHP中判断矩阵一致性改进的一种新方法［J］.系统工程理论与实践，2000（2）:123-126.

［29］李玲娟，豆坤.层次分析法中判断矩阵的一致性研究［J］.计算机技术与发展，2009（10）:131-133.

［30］黄德才，胥琳.AHP法中判断矩阵的比例标度构造法［J］.控制与决策，2002（4）:484-486.

［31］孙昭文，杨俊行，李莉.层次分析法的判断矩阵一致性及其应用［J］.天津大学学报，1994（4）:487-493.

［32］刘卫国.MATLAB程序设计教程［M］.北京:中国水利水电出版社，2010.

Research of Water Resources Carrying Capacity based on the Fuzzy Analytic Hierarchy Process

WANG Hai-liang1,YANG Yong-hong1，ZHANG Ying2
（1.Tibet Agriculture and Animal Husbandry College，Linzhi 860000，China；
2.Hebei Research Institute of Investigation&Design of Water Conservancy&Hydropower,Tianjin 300250，China）

According to the actual situation of water resources in Linzhi area，a hierarchical structure model of water resources carrying capacity was built up.Five indexes were consisted of in the criterion layer and fifteen indicators were selected in the factor layer.Evaluation of water resources carrying capacity in Linzhi area was carried out.In the process of evaluation，the analytic hierarchy process and the fuzzy evaluation were combined，and the mathematical models were established.Programs were written using Matlab software.The final score of fuzzy evaluation were shown.At last，we found water resources carrying capacity is in good state.

analytic hierarchy process；fuzzy evaluation；water resources carrying capacity；linzhi area

TV139.16

B

1672-9900（2014）03-0016-05

2014-03-12

西藏自治区自然科学基金项目：“西藏土地水动力参数尺度效应和空间变异性研究”

王海亮（1988-），男（汉族），河北唐山人，硕士，主要从事西藏高原水利及节水灌溉研究，（Tel）18989041350。