基于过采样的六二阶归一化累积量盲均衡算法

张晓琴，胡永生，张立毅

（1.天津商业大学信息工程学院 天津300134；2.天津大学电子信息工程学院 天津300072；3.滨州学院信息工程系 滨州256603）

1 引言

盲均衡主要用于无线通信系统中发送信号和信道未知的情况。信道中振幅和相位的衰落、多径干扰等均会引起码间干扰，严重影响通信效果。因此，为了消除码间干扰的影响，专家和学者们提出了多种盲均衡算法[1]。1991年，Tong[2]等人实现了只利用接收信号的二阶循环统计量完成信道的盲均衡，开创了基于二阶循环统计量盲均衡研究的先河。目前基于二阶循环统计的算法，大体可以分为两类[3]。一类是优化相关函数（谱）方法[4,5]，借助信道与接收信号之间的相关性构建函数，利用优化方法搜索信道参数，但不可避免地存在局部最优问题；另一类是基于特征结构的算法[6,7]，其特点是不存在局部最小问题，但需要先对信道进行一系列的假设，然后对接收信号的相关矩阵采用奇异值分解、特征值分解和QR分解等来辨识和均衡信道，使得算法较复杂，难于在线处理。因此，本文提出一种新的基于过采样的六二阶归一化累积量的盲均衡算法。在接收端首先对接收信号进行过采样，降低噪声，补偿信道失真[8]，然后将六二阶归一化累积量作为代价函数，采用最陡下降法进行迭代求解，最后对数据进行抽取，恢复发送序列。

2 基于过采样的归一化累积量盲均衡算法的原理

2.1 基于过采样的盲均衡算法的原理

基于过采样的盲均衡算法原理如图1所示。图中，x(n)为发送信号，h(n)为未知信道的冲激响应，v(n)为叠加高斯白噪声，y(n)为过采样后接收到的信号，w(n)为盲均衡器的抽头系数，P和P分别表示以T/P间隔进行过采样和以P倍速率抽取， 为抽取后的输出信号， 为判决后的输出信号。

图1 基于过采样的盲均衡算法原理

从图1中看到：

*为卷积运算。如果过采样频率是波特采样频率的P倍，在过采样后接收到的样本数是原来接收样本的P倍，增加了数据量，但总的噪声能量不变，输出量化噪声的基线降低，量化噪声分散在更宽的频率范围里，输出信号的信噪比得到改善。过采样技术还能避免因欠采样引起的频谱混叠，因而可有效补偿信道畸变[8]。

2.2 归一化累积量盲均衡算法的原理

信道均衡问题可以表达为：设计和调整均衡器的抽头系数w(n)，使得信道的总响应s(n)=h(n)*w(n)呈现（延时的）δ脉冲响应，即：

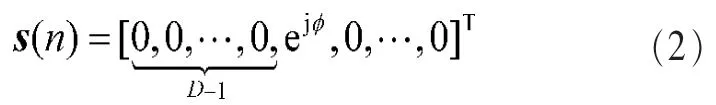
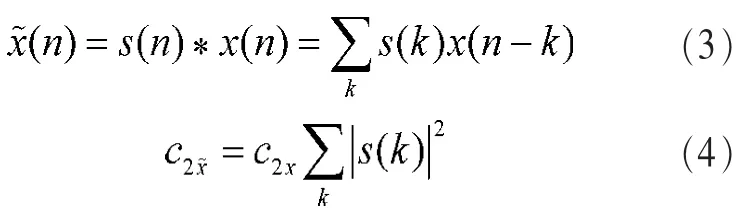
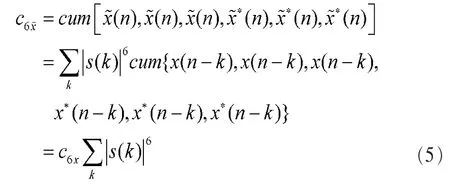
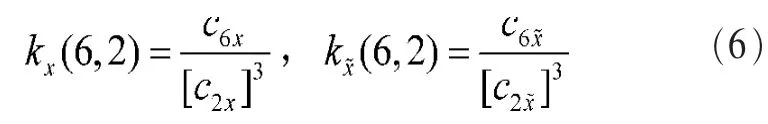
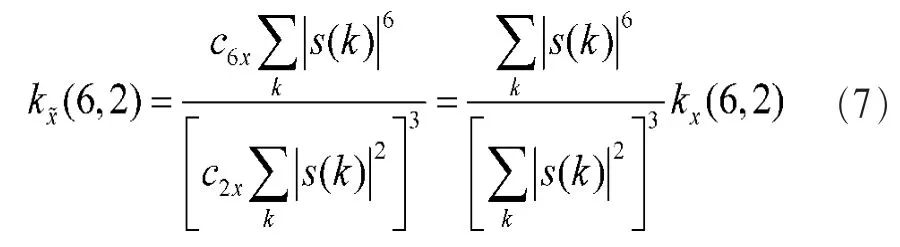
根据Gadzow归一化准则[10]，如果系统的总响应s(n)中只有一个非零元，即满足式（2），则系统输入、输出归一化累积量幅度相等是实现盲均衡的充要条件。这样就把盲均衡问题转化为求解的六二阶归一化累积量的极大值问题。

2.3 基于过采样的六二阶归一化累积量盲均衡原理

定义的六二阶归一化累积量为代价函数：

利用最陡梯度下降法，可以得到均衡器抽头系数的迭代计算式为：

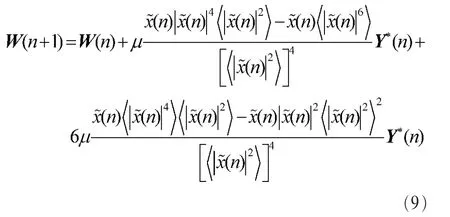
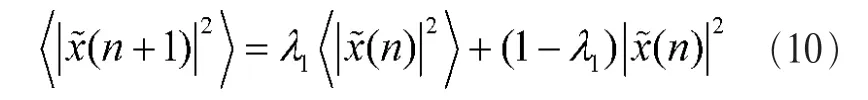
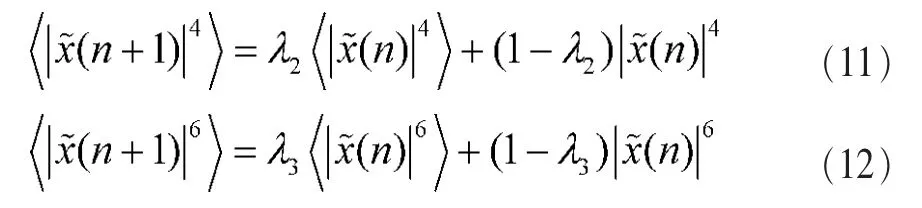
这里，0<λ1,λ2,λ3<1是遗忘因子。

通常，迭代步长μ为一个恒定值，本文采用变步长μ(n)来代替固定步长μ，即在算法初始加大步长，加快收敛速度，随着算法的收敛，减小步长，减小稳态剩余误差。本文采用误差的四阶累积量C4e作为步长控制因子，即：

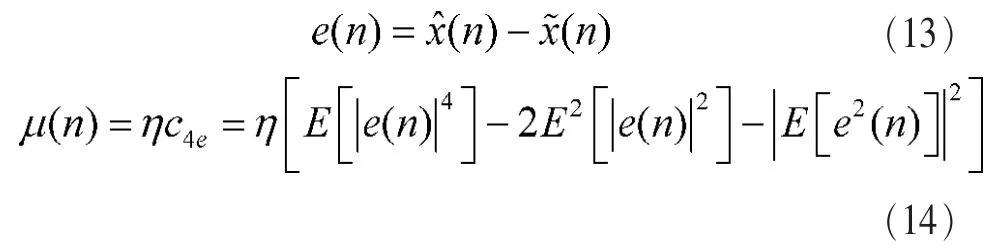
这里，η是比例因子。

3 计算机仿真

采用16QAM信号，均衡器采用横向滤波器，其阶数为11，信道叠加均值为零的高斯白噪声，信噪比SNR=20 dB，信道采用典型电话信道，其冲激响应为[11]：

图2给出采用16QAM信号对波特率采样且固定步长（图2（a））和变步长（图2（b））、T/4过采样且固定步长（图2（c））和变步长（图2（d））进行均衡算法仿真的星座图。从图中可以看出，T/4过采样变步长算法的星座图更清晰 和 集 中。图 中，μ=0.000 06、λ1=0.997、λ2=0.997、λ3=0.998 2、η=-0.000 08。

图2 4种过采样归一化累积量盲均衡算法的星座图

图3为T/4过采样变步长算法误差e(n)的四阶累积量C4e，从图中看出，随着算法的收敛，误差的四阶累积量逐渐减小，符合变步长的要求。

图3 步长变化曲线

图4 是4种算法的收敛曲线，从图中可以看出，基于T/4过采样的变步长算法收敛最快，且T/4过采样后的两种算法在收敛后稳态剩余误差非常小，达到0.005左右。图5是4种算法的误码率曲线，可以看出，基于T/4过采样变步长算法的误码率明显低于其他3种算法。

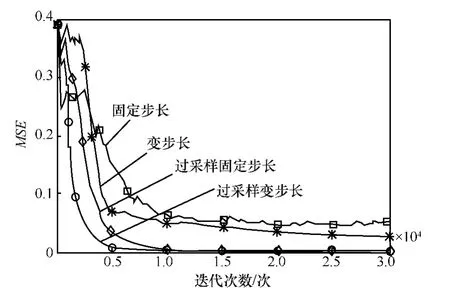
图4 4种算法的收敛曲线

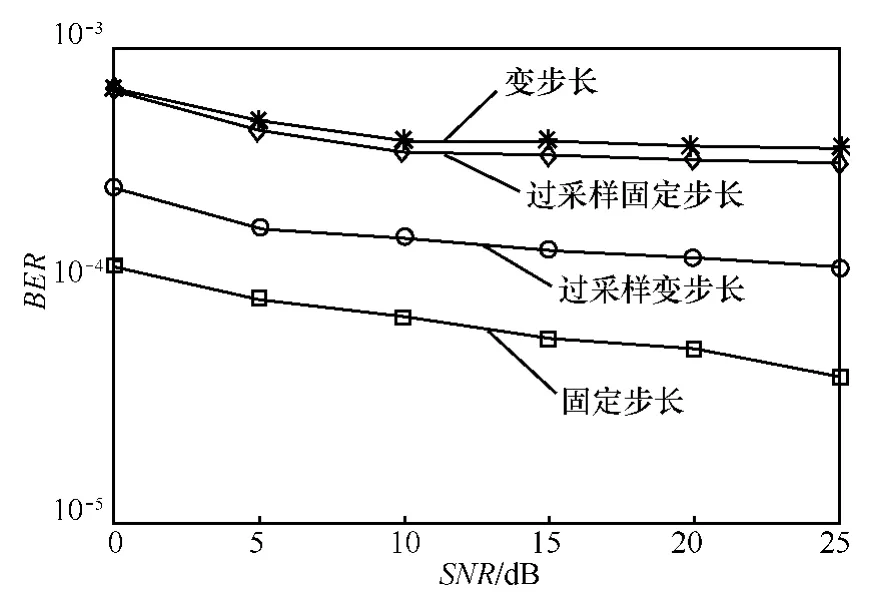
图5 4种算法的误码率曲线

4 结束语

本文根据过采样后信号的特性，设计了一个基于高阶累积量的盲均衡算法，同时加入变步长思想，不仅使得算法实现了全局最优，也加快了收敛速度、减小了稳态剩余误差，同时消除了噪声影响，但运算复杂度较高。本文的六阶累积量是基于对称分布、均值为零且统计独立的信号推导出来的，目前通信中的大部分信号符合这样的特点，所以算法复杂度并没有增加太多。计算机仿真表明，本算法有较快的收敛速度、较低的误码率及较好的收敛效果。

1 张立毅．数字通信系统中盲均衡技术的研究．北京理工大学博士学位论文，2003

2 Tong L,Liu R W,Soon V C,et al.Indeterminacy and identifiability of blind identification.IEEE Transactions on Circuits and Systems,1991,38(5):499～509

3 Li X H,Fan H H.QR factorization based blind channel identification with second-order statistics.IEEE Transactions on Signal Processing,2000,48(1):60～69

4 李长荣，吴迪．水声信道盲均衡优化仿真研究．计算机仿真，2013，30（7）：183～186

5 乔艳涛，张立军．利用确定性信道盲估计改善DFE均衡器的收敛特性．通信学报，2005，26（6）：74～79

6 陈炯芳，林荣，韦岗．基于输出过采样的IIR信道迫零盲均衡．电子学报，2006，34（3）：441～444

7 王永川，陈自力．基于冗余预编码的STBC-SC-FDE系统的频率域盲信道估计．通信学报，2013，34（1）：185～190

8 张贤达，保铮．通信信号处理．北京：国防工业出版社，2000

9 邹谋炎．反卷积和信号复原．北京：国防工业出版社，2001

10 Cadzow J A.Blind deconvolution via cumulant extrema.IEEE Signal Processing Magazine,1996,13(3):24～42

11 张晓琴，张立毅．基于T/4分数间隔采样双模式盲均衡算法的研究．电路与系统学报，2012，17（1）：81～85