基于城市区域发展的劳瑞模型动态改进

王力生，帅 斌

(西南交通大学 交通运输与物流学院，四川 成都 610031)

集聚效应是城市经济发展过程中表现出来的企业和人口集中化现象，有利于提高资源和公共物品的配置效率以及降低生产成本[1]。与此同时，城市土地资源作为一种不可再生的生产要素，其价值会随着不同区位的集聚程度而变化。城市居民和厂商根据不同的集聚效应和土地价值进行选址活动，引起城市空间布局的内部调整和外表扩张现象[2]。随着我国经济产业结构调整，传统的制造业开始远离市中心向城市外围或其它地区迁移，以金融、商业和服务业为代表的第三产业逐渐成为大城市的主导产业。城市中心区土地价值的持续升值，也迫使人口居住地向郊区扩张，造成居住地和就业场所日益分离[3]。因此，研究城市区域经济发展对人口和就业等空间布局的作用机理具有重要意义。

劳瑞模型是交通规划中研究土地利用的基础模型，由美国交通学者劳瑞于1964年研究匹兹堡交通规划问题时提出。其最主要的价值在于用数学方法探讨了十分基础的城市就业和人口分布等问题，使与之相关的城市土地利用和区位理论得以定量化研究。劳瑞模型作为研究交通规划问题的基础模型，从它提出开始就得到了许多学者的研究改进，其中最主要的两个方向是对模型的动态改进和经济改进[4]。动态改进主要指在城市发展过程中，基础产业发生变化如何引起人口分布的变化；经济改进则研究如何确定基础产业与服务产业之间的关系。笔者通过对原始劳瑞模型、Garin矩阵改进模型以及Rogers动态改进模型基本思想的研究，在Rogers动态模型基础上，引入种群生长模型模拟城市区域基础产业发展，提出在城市土地和人口等资源限制条件下，区域经济发展对人口和就业布局的影响模型。

1 劳瑞模型及其改进形式

1.1 原始劳瑞模型

原始劳瑞模型[5]的基本思想是：将研究区域划分为若干个小区，每个小区存在一定已知数量的基础产业(如市政部门、学校和工厂等)，基础产业带来就业数量并引起就业人口在研究区域的分布(理解为不同小区的人口数量)；另一方面，基础产业就业人口产生对服务业的需求，引起服务产业在研究区域的分布，服务产业同样会带来就业增加，并形成新的人口分布，因此，最终的人口和产业分布产生于上述“循环过程”的均衡或在人口和土地限制条件下的极限情况。

为求解模型，劳瑞给出的算法思路[6]是将小区的就业数量看成该小区的吸引力函数，而人口分布则表示为小区就业数量和吸引力的函数，通过一次迭代计算可求出一个人口及就业分布，并对计算结果进行是否满足人口和土地等限制条件的检验，直到求出满足限制条件的最优解(即最大人口和就业分布)。

通过以上分析，不难发现原始劳瑞模型存在以下两个最为突出的问题：

1)劳瑞模型在求解过程中并不考虑土地和人口等限制条件约束，而是对计算结果进行检验，因此求出的解有可能部分满足限制条件(即有的小区满足人口和土地限制，而另外的小区不满足)，这种情况下模型无解；另一方面，每进行一次迭代计算，都要对结果进行检验，这将是十分繁琐的；

2)劳瑞模型只是解决了一定已知基础产业分布条件下的最终人口和就业分布情况，这实际上是一个静态的过程，因为城市经济和人口的增长必然会引起基础产业的变化，由此引出劳瑞模型的动态改进形式。

1.2 劳瑞模型改进形式

R.A.Garin[7]在原始劳瑞模型的基础上，引入向量描述人口和就业分布，并通过矩阵表达劳瑞模型中的函数关系，这样劳瑞模型的迭代计算过程变为矩阵的计算，从而使模型大大简化。值得注意的是，Garin模型并未改变劳瑞模型的“静态”属性，其收敛条件的确定来源于级数求和的数学证明，未考虑实际的土地和人口限制条件。

与本文密切相关的是Rogers 模型，由A.Rogers[8]在Garin模型的基础上引入增长矩阵G进行动态建模。基本思想是：给定一个基础产业增长矩阵G，引入时间变量t，建立基础产业与时间t的函数关系，从而对于不同的时间t，可求出相应的人口分布。模型的终止条件是迭代过程产生人口和时间t的线性关系，表示人口达到稳定增长状态；同理，对于就业也可建立相应的迭代关系，求得就业增长率，由此Rogers通过该模型分析了人口和就业之间的关系。但是，Rogers 模型仍存在许多亟待修改的问题：首先，模型中基础产业增长矩阵G是人为给定的并且与时间t无关，与实际情况并不相符；其次，人口按稳定的速率增长意味着人口无限的增多，势必违反劳瑞模型中人口和土地的限制条件。对上述两个问题的深入探讨，是笔者提出动态改进模型的基础。

2 改进模型

2.1 改进模型的出发点

针对上述各个模型存在的问题，提出劳瑞模型的另一种动态改进模型，主要从以下3个方面考虑：

1)如何将原始劳瑞模型中的限制条件通过模型本身的约束条件表示出来，使模型求得的解一定符合人口和土地因素等限制；

2)如何确定与时间相关的动态增长矩阵，反映城市区域经济随时间发展的情形；

3)对模型的边界值即稳定状态探讨，保证模型的解一定是满足约束条件的最优解。

2.2 改进模型

首先，将研究区域划分成n个小区，对每个小区编号1，2，…，n；那么时间为t时的基础产业分布可表示为：

(1)

按照Garin模型中的结论[7]，一定的基础产业分布最终会决定相应的人口分布Pt和就业分布Et，它们满足关系：

(2)

(3)

这里着重探讨一下矩阵A，B的含义与计算问题。矩阵A可看成就业-人口生成矩阵，表示由就业引起人口分布的“生成关系”(参考式(3)的第1个等式)，具体计算公式为：

A=[aij′][ai]

(4)

式中：[ai]表示对角矩阵diag(ai)，其元素ai表示i小区就业人口占总人口的比重；矩阵[aij′]的元素aij′表示“到家旅程函数”(a journey to home function)[7]。

不同的构造会产生不同的迭代结果，这里将“到家旅程函数”表述为在小区i工作的人口居住在小区j(j=1，2，…，n)的概率，计算方法参照Logit模型的解法[5]，选取距离、土地价格、就业岗位等因素xk(k=1，2，…，m)建立效用函数：

(5)

值得注意的是，Garin模型求得的解有可能不满足约束条件，原因在于效用函数中参数xk的不同取值会造成不同小区人口和就业分布的变动。一个明显的事实是，如果xk中考虑j小区的拥挤情况的话会使结果满足人口和土地限制条件。

同理，矩阵B可看成人口-就业生成矩阵，表示一定的人口分布产生相应的服务需求，计算过程同A，那么B的计算表示为：

B=[bij′][bi]

(6)

(7)

从另一个角度考虑，基础产业的增长，一方面受规模效应的影响，即开始阶段由于产业配套设施和产能等尚未完善，发展比较缓慢；随着建设发展，规模效应逐渐显现出来，增长速度变快；最后，区域发展完善，土地和人口限制作用表现出来，经济达到饱和状态，增速放缓。因此可考虑用种群生长模型对其进行模拟，即：

(8)

式中：λ表示增长系数矩阵。

就其计算方法而言，一般应通过实际调查，收集城市不同区域基础产业和社会经济发展等数据进行线性回归求解[9]，使计算结果尽可能拟合实际情况；M表示n维对角方阵，其对角线上的元素由每个小区的基础产业用地限制与该小区基础产业数量之差。化简得：

(9)

式中：E(l)b表示基础产业最大分布向量，其计算通过式(12)给出。

联立式(7)和式(9)得：

(10)

(11)

式中：X，Y，Z为对角矩阵，元素分别表示基础产业、服务产业和单位人口的用地面积；S，Su分别表示区域总面积和不能利用的土地面积。

因此，E(l)b的求解表述为以下线性规划问题：

MaxE(l)b

s.t.E(l)bX+E(l)b(I-AB)-1Y+

E(l)b(I-AB)-1AZ≤S-Su

E(l)b≥0

(12)

通过上述模型，可解出3个变量Gt，Et和Pt。其中：Gt反映了不同小区基础产业的增长率，也即区域经济发展的速度；Et和Pt则分别反映城市随着时间t不断变化着的人口和就业分布。

2.3 算 法

由上述模型分析可知，该模型算法本质上是一个迭代过程，表述如下：

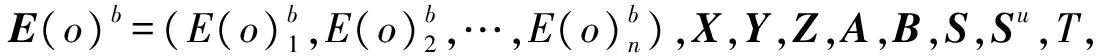
Step 3：判断t≤T，若是则转Step2，否则转入Step4；

Step 4：终止算法，输出Et，Pt，Gt。

值得注意的是，A，B为实际调查数据计算的结果，与其它输入无关，因此作为已知数据给出；λ在模型中采取近似算法，参考式(13)；T为给定时间长度，可理解为规划年限，当T趋向于无穷大时，可计算模型的边界人口和就业分布。

3 算 例

式中：tij表示从小区i到j的距离，且tij由下述矩阵给出(注：tij=tji，表中没有列出)。

表1 小区距离数据Table 1 Distance data between zones

(续表1)

1234567891042．006．0010．505．366．009．0010．7251．504．5011．363．006．007．7262．0015．226．683．863．8672．008．3611．3613．0882．003．004．7291．501．72102．00

矩阵[a]中对角元素取值为5，[b]中对角元素取值为0.2。

初始条件：

E(o)b=[4 500,5 000,3 000,2 500,3 500,

9 000,3 000,2 000,3 000,4 000]

土地限制矩阵S-Su取为行向量s(数据单位：km2)：s=[18,22,16,15,20,30,15,17,19,20]

X，Y，Z矩阵分别取对角元素为10，3，1的对角矩阵(数据单位：m2)。

由式(12)可求出各小区基础产业限制向量E(l)b：

E(l)b=[8 746,11 513,6 028,6 196,8 789,

17 369,7 485,6 746,8 620,9 939]

对于系数矩阵λ的计算，在本模型中采用式(13)近似计算：

λ=diag((E(l)b-E(o)b)./[E(o)b(E(l)b-

(13)

在MATLAB R2011a环境下，对模型进行了模拟求解：

1)取增长系数矩阵λ=λ1,λ2,λ3对模型进行模拟，讨论不同系数矩阵对模型收敛的影响(此时最佳增长系数矩阵λ1取值参考式(13)且取T=10)。

λ1=diag(0.222 2,0.2,0.333 3,0.4,0.285 7,0.111 1,0.333 3,0.5,0.333 3,0.25)×10-4

λ2=diag(0.3,0.4,0.3,0.5,0.3,0.4,0.3,0.2,

0.3,0.4)×10-4

λ3=diag(0.3,0.4,0.3,0.5,0.3,0.4,0.3,0.2,

0.3,0.4)×10-5

图1表明在增长系数矩阵λ取最佳值时(即λ=λ1)各小区基础设施建设发展比较稳定，且以正常速度收敛于限制曲线；若增长系数矩阵λ取值过大(即λ=λ2)，虽然收敛于限制曲线的速度较快，但是各小区发展不平衡；若增长系数矩阵λ取值过小(即λ=λ3)，则以较慢的速度收敛于限制曲线。

图1 不同增长系数矩阵下的基础产业随时间变化情况Fig.1 Basic-industry variation with time underdifferent growth factors

2)为叙述的简便，只给出小区j=1在上述模型下人口的长期形态，并检验其是否收敛于一个极限值，其它小区人口极限分布同理可求。

由图2可知，在t﹡=6时人口基本上达到极值41 357，值得注意的是，理论上达到极值点对应的时间t﹡应该等于确定最佳增长系数矩阵λ所取的时间t。图2中t﹡≠t(t=10)，主要是由绘图时人口数量坐标轴坐标间隔太大造成的。

图2 人口随时间变化Fig.2 Population variation with time

3)考虑增长矩阵Gt与时间的关系，确定各个时期的基础设施建设速度，为绘图的方便，在不影响结果的情况下把增长矩阵Gt转换为向量。

由图3可以看出两个明显的规律：①随着时间的增加，增长矩阵取值越来越小，表明就长期而言，基础设施总量上逐步增加，但增速逐渐变慢；②增长矩阵(向量)曲线越来越平，说明就长期而言，各小区逐步开发完善，人口和土地等得到充分利用。

图3 增长矩阵随时间变化Fig.3 Increasing matrix variation with time

4 结论及展望

从算例的模拟结果来看，最终就业分布Et和人口分布Pt较好的满足了原始劳瑞模型中有关人口和土地的限制条件，并给出了动态增长矩阵Gt的算法及其现实含义：即城市经济发展过程对不同区域基础设施的投资应该具有怎样的规律，以便达到城市总体发展均衡性的要求。但是，有关模型中参数的计算还值得进一步研究，如增长系数矩阵λ最佳值的求解，一般而言要通过搜集实际数据做回归分析，算例中只提供了考虑时间因素的近似算法。

在实际的城市发展过程中，包含两个方面的内容：①对既有的区域进行结构调整(如居民区重建、产业搬迁等)；②进行城市扩张，实现多区域中心发展。对于结构调整而言，本模型可用于分析调整前后人口和就业的分布情况；对于城市扩张，本模型可用于研究新区投资对人口和就业的吸引。

本模型的建立可以看成两个过程：①人口和就业的产生；②人口在空间的分配。其中人口和就业的产生是一个自增长的过程，即一定的人口需求产生一定的就业岗位，就业又会引起新的人口增长。人口在空间的分布通过构建Logit模型，给出人口对居住区域选择的概率分布。因此，为使模型更好的模拟现实城市区域发展与人口、就业分布情形，需要对人口和就业生产模型及人口分配模型进行更加深入的研究。

[1] 龚维永,高建杰,焦海贤.交通空间需求交通系统与土地利用关系探讨[J].重庆交通大学学报:社会科学版,2010,10(6):20-22.

Gong Weiyong,Gao Jianjie,Jiao Haiyan.Discussion on the relationship between spatial traffic demand,traffic system and land-use[J].Journal of Chongqing Jiaotong University:Social Sciences,2010,10(6):20-22.

[2] 李孟学.城市空间结构研究现状及展望[J].赤峰学院学报:自然科学版,2013,29(3):131-134.

Li Mengxue.Research status and prospects on urban spatial structure[J].Journal of Chifeng University:Natural Science,2013,29(3):131-134.

[3] 龚维永,高建杰,焦海贤.城市交通空间需求与交通网络双均衡研究[J].重庆交通大学学报:自然科学版,2011,30(3):429-432.

Gong Weiyong,Gao Jianjie,Jiao Haiyan.Study on the bi-directional equalization between urban traffic spatial demands and networks[J].Journal of Chongqing Jiaotong University:Natural Sciences,2011,30(3):429-432.

[4] 陈佩红,王稼琼.交通与土地利用模型—劳瑞模型的理论基础及改进形式[J].生产力研究,2007(14):39-44.

Chen Peihong,Wang Jiaqiong.Traffic and using-land model—theoretical basis and improvment of the lowry model[J].Productivity Reserch,2007(14):39-44.

[5] 陆化普.交通规划理论与方法[M].北京:清华大学出版社,1998.

Lu Huapu.Theory and Method on Transportation Planning[M].Beijing:Tsinghua University Press,1998.

[6] Hutchinson B,Batty M.从城市物质模型到经济模型——劳瑞模型结构的修正[J].杨涛,彭爱新,译.国外城市规划,1996(2):39-44.

Hutchinson B,Batty M.Lowry model improving—based on urban substance and economy[J].Yang Tao,Peng Aixin,translation.Urban Planning Overseas,1996(2):39-44.

[7] Garin R A.A matrix formulation of lowry model for intra-metropolitan activity allocation[J].Journal of the American Institute of Planner,1966,32(4):361-364.

[8] Rogers A.A note on the garin-lowry model[J].Journal of the American Institute of Planners,1966,32(6):364-366.

[9] Giordano F R,Weir M D,Fox W.数学建模入门[M].叶其孝,姜启源,译.北京:机械工业出版社,2005.

Giordano F R,Weir M D,Fox W.A First Course in Mathematic Modeling[M].Ye Qixiao,Jiang Qiyuan,translation.Beijing:China Machine Press,2005.