基于一阶循环均值算法的VHF频段信号调制分类识别方法研究*

杨发权，李 赞，罗中良

（1.佛山科学技术学院 佛山528000；2.西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安710071；3.惠州学院 惠州516007）

1 引言

VHF频段广泛用于军事和民用通信中，如电力、水利、气象、石油、林业、勘探、煤矿、铁路等行业，采用的调制方式主要包括AM、ASK、FM、FSK、DSB、SSB、单载波线性数字调制（SCLD）（如PSK、QAM）及循环前缀单载波线性数字调制（CP-SCLD）等，以实现通信、遥控、遥测、遥感、区域报警系统的数字信号传输。因而对该频段信号进行调制识别以实现对通信信号的监控、信号确认、干扰辨识、电子救援及军事威胁分析等，具有十分重要的意义[1,2]。

调制识别过程包括信号预处理、特征提取和分类识别3部分。信号预处理主要是为后续处理提供合适的数据，一般包括频率下变频、同向和正交分量分解、载波频率和信号速率估计以及多径信道均衡等；特征提取是从输入的信号序列中提取对调制识别有用的信息，得到最能反映差别的特征；分类识别主要是判断信号调制类型的从属关系[3,4]。其中，特征值的提取目前主要采用的方法是分别提取瞬时频域特征值、时域特征值，分析高阶原点矩、高阶累积量、小波变换、谱相关、循环谱相关、功率谱、星座图、信号的峭度等[5～8]，并且取得了不错的识别效果。但随着信号环境的日益复杂，在高斯白噪声严重干扰、相位频率失真及时延等多种情况下，如何在现有识别技术方法的基础上不断创新、提高分类识别率仍然是一项颇具挑战性的研究课题[9]。为此，本文采用信号的一阶循环平稳特性，提出一阶循环均值算法，用于VHF频段信号的调制分类识别，该算法不需要知道信号载波频率、信号带宽等信息，在信噪比很低的情况下，有较高的分类识别率。

2 一阶循环平稳识别特征参数

采用的一阶循环平稳识别参数主要有：一阶循环频率系列（CFS）、一阶循环均值（CM）及CM的绝对值等。

其中，k={α：mr（α）≠0}为一阶循环频率系列，mr（α）代表一阶循环频率为时对应的一阶循环均值。对于具体信号，如某连续信号r（t），经速率fS抽样后所得信号为其一阶循环均值与一阶循环频率系列之间的关系为：

一阶循环频率为α时，一阶循环均值与抽样次数k的关系[10]为：

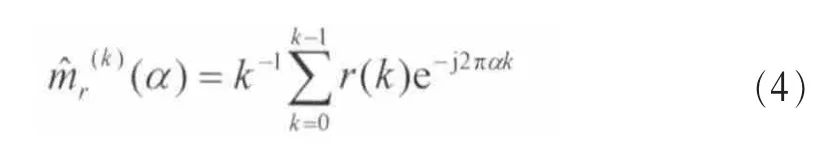
对于VHF频段各信号（如FSK或FM信号），以FSK为例，如果频偏Δf=，n为整数，则FSK信号具有一阶循环平稳特性，在一阶循环频率为α时，一阶循环均值及一阶循环频率系列分别为：

可见，非一阶循环频率对应的一阶循环均值等于0。在一阶循环频率为α时，一阶循环均值与调制阶数M、相位θ、时延t0、频偏Δf及信噪比有关，根据式（5）一阶循环均值的绝对值为：

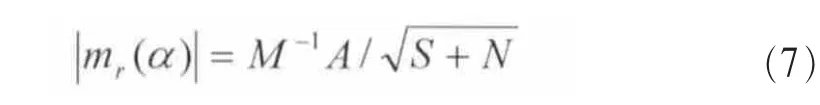
该值与调制阶数M和信噪比有关，随着调制阶数M的提高而下降，随着信噪比的下降而下降。根据式(6)，一阶循环频率数目等于调制阶数M，对于任何阶数M，一阶循环频率与频率频偏Δf、抽样频率fS有关，两个相邻一阶循环频率间隙等于2fΔ。

对于VHF频段中的AM或ASK信号，以AM信号为例，一阶循环频率为α时，一阶循环均值和一阶循环频率系列可分别表示如下：

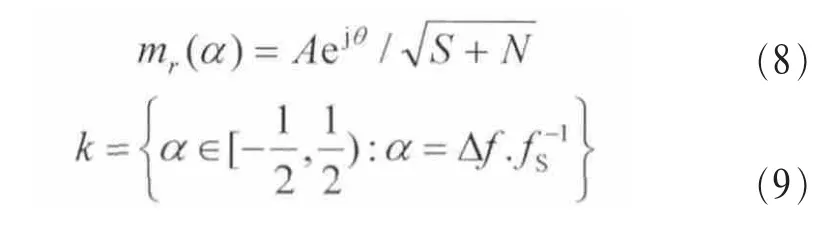
根据式（8），一阶循环频率为α时，一阶循环均值的绝对值为：

对于VHF频段中的SCLD及CP-SCLD信号，其n阶平稳时间参数用封闭形式表达，则一阶循环频率为α时，一阶循环均值可表示为[11]：

其中，mS为信号星座图各点的一阶均值，ρ为过抽样因子，对于星座图对称信号（如PSK和QAM信号），mS为0，对于任何一阶循环频率，一阶循环均值均等于0。

对于VHF频段其他信号（如DSB、SSB信号及噪声），其w（t）是零均值的静态过程，不呈现一阶循环特性，因此一阶循环均值不存在[12]。

3 一阶循环均值识别算法及识别步骤

3.1 一阶循环均值识别算法

本文采用的一阶循环均值识别算法的步骤介绍如下。

（1）估测信号在一阶循环频率系列α′时一阶循环均值的绝对值及在标准带宽和抽样速率一定的情况下在相同观察时间间隙内观察到k个样品的偏差范围。设定信噪比低于某值（设为SNRco）时，对应的一阶循环均值的绝对值为截止值，用Vco表示，当一阶循环均值的绝对值高于或等于Vco时，对应的一阶循环频率被选为算法下一步的检测循环频率（即候选循环频率）。当信噪比比SNRco高很多时，检测所有一阶循环频率系列对应循环均值的绝对值峰值；当信噪比比SNRco低很多时，由于对应循环均值的绝对值小于Vco，因而被忽略。

（2）检查（1）中选择的候选循环频率值是否属于一阶循环频率系列；估测每个循环频率对应的一阶循环均值统计值，并与截止值进行比较，若在候选的循环频率前提下其一阶循环均值超过截止值，则所选择的循环频率数目可用于信号的分类与识别。

3.2 识别步骤

根据上述识别算法对VHF频段信号进行分类识别，具体步骤如下：

（1）对待分类识别信号进行滤除带外噪声、下变频及标准数字化处理；

（2）估测在标准抽样频率和信号带宽范围内，一阶循环频率系列候选频率对应的一阶循环均值；

（3）选择一阶循环均值绝对值超过Vco时对应的一阶循环系列候选循环频率；

（4）通过循环平稳测试决定选择一阶候选循环频率数目；

（5）根据候选一阶循环频率数目实现对VHF频段信号（包 括AM、ASK、MASK、FM、2FSK、MFSK、DSB、SSB、SCLD、CP-SCLD等）的分类识别。这样在接收端如果检测到单个一阶循环频率，可判断接收信号为AM和ASK；如果检测到两个一阶循环频率，可判断接收信号为2FSK；如果检测到一阶循环频率为（2m-1+1，2m）内的某数目M，可判断接收信号为MFSK（M=2m，M≥4）；如果没有检测到一阶循环频率，则接收信号可识别为DSB、SSB、SCLD、CP-SCLD。

4 识别方法性能理论

第3.2节算法中第（2）步主要采用平稳性测试方法寻找一阶循环频率及其数目，并把这些频率作为一阶循环候选频率，这些频率对应的一阶循环均值绝对值大于Vco，理论上在信噪比低于SNRco时，长数据序列一阶循环均值绝对值均低于Vco，所以算法中通过平稳测试方法不可能找到相应的一阶循环频率，因而对信号的分类识别率为0；当信噪比大于SNRco时，则可检测到所有的一阶循环频率，这样对AM或ASK信号的分类识别率等于算法中通过平稳测试的概率，即通过一阶循环频率测试的概率为：

对于2FSK和MFSK信号的分类识别，检测一阶循环频率数目为2时的概率和一阶循环频率在（2m-1+1，2m）个数的概率，即：

其中，P（N）是检测N阶循环频率的概率。对于DSB、SSB、SCLD、CP-SCLD等信号，在理论上由于算法中的第（1）步无法选择一阶候选循环频率，在算法第（2）步中就自然无法检测到一阶候选循环频率个数，因此对这些信号在VHF频段的分类识别概率为1。

5 仿真结果与硬件实现

采用MFSK和AM信号进行识别仿真，其中MFSK中的M分 别 取2、4、8，波特率分别为1.5 kHz、0.75 kHz、0.375 kHz，频偏均为1/T（n=1）；AM信号取带宽为3 kHz，接收端MFSK和AM信号功率相同，观察时间间隙为1 s。调制信号m（t）由均值为0的高斯随机序列经过低通滤波器产生，取调制指数μA=0.3。设载波相位为θ，θ值在（-π，π）服从均匀分布，频偏Δf=2 400 Hz。MFSK时延t0=0.6T，AM信号时延t0=10 fS-1，接收信号抽样速率fS=48 kHz，截止值Vco=0.05，仿真实验次数取1 000次。

5.1 一阶循环均值绝对值与候选循环频率的关系

在信噪比分别为20 dB、0、-13 dB和-20 dB时，4FSK信号一阶循环均值的绝对值与对应候选循环频率α′关系的仿真结果如图1所示。

图1中α′的取值范围为[-0.4,0.4]，随着信噪比的下降，一阶循环均值绝对值在α′=α处的波峰逐步下降直至 波峰不显眼。在α′≠α处，由式（7）可 得 到SNRco值为-13.8 dB，在信噪比为20 dB时，在一阶循环频率α处的一阶循环均值绝对值为0.25左右，和理论分析结果一致。

当信噪比比SNRco大很多时，如图1(a)、图1(b)所示，所有一阶循环频率对应的一阶循环均值绝对值高于截止值0.05；当信噪比在SNRco值附近或者比SNRco小很多时，对应的一阶循环均值绝对值均低于截止值0.05，如图1(c)、图1(d)所示。

在信噪比为20 dB时，AM、2FSK、2PSK和噪声信号一阶循环均值的绝对值与对应候选循环频率α′关系的仿真结果如图2所示。

从图2可知，AM和2FSK信号在α′≠α处的一阶循环均值绝对值分别为1和0.5左右，而2PSK信号和噪声则没有这样的波峰，并且其一阶循环均值绝对值小于截止值0.05。

5.2 调制分类识别率

在相同的观察时间间隙内，信噪比不同的情况下，对VHF频段中的AM、2FSK、4FSK、8FSK等信号进行调制识别分类，仿真结果如图3所示。

比较图3(a)和图3(b)知，对于AM和2FSK信号，在信噪比较低的情况下就可以获得较好的识别性能；对于4FSK、8FSK信号，分类识别率则差些，这是由于相同时间间隙内，阶数越高，在接收端观察到的数据序列符号数目越少，使估测一阶循环均值的精确度下降，导致很多一阶循环频率被遗漏，因而在缺乏足够一阶循环频率先验信息的情况下，识别分类的性能下降。仿真结果与理论分析性能十分接近，特别是在信噪比远大于SNRco值时，分类识别性能较好。

图1 4FSK信号一阶循环均值绝对值与候选循环频率的关系

图2 AM、2FSK和2PSK信号一阶循环均值绝对值与对应候选循环频率的关系

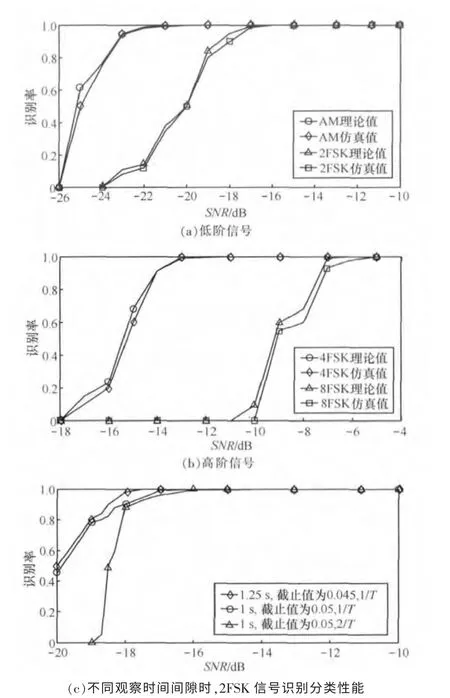
图3 调制分类识别仿真

图3(c)是在不同的观察时间间隙内得到的2FSK信号的识别分类性能。当观察时间间隙较长时，观察到的符号序列数目较多，在设置较低的截止值、允许减少相应SNRco值的情况下，也可获得较好的识别性能，反之随着截止值的增加，在识别性能相同的情况下需要的信噪比增加。另外，在观察时间间隙相同时，识别性能与频偏有关，频偏越小，识别性能越好。

5.3 硬件实现

硬件主要采用射频信号发生器、A/D采集板、FPGA板、DSP开发板等实现。其中，射频信号发生器采用美国IFR公司生产的型号为IFRZO31的射频信号发生器，目的是产生实验需要识别的VHF频段中的AM、2FSK、4FSK、8FSK等各种调制信号；A/D采集板的主要作用是把射频信号发生器产生的调制信号通过A/D转换，得到数字调制信号的离散采样值，主芯片采用Analog Device公司生产的AD9411-200，主要指标为具有200 Mbit/s的最高采样频率；FPGA的主要作用是利用FPGA板上50 MHz晶振通过内部倍频为A/D采集板提供200 MHz的时钟频率，同时对A/D采样之后传输的数据进行临时存储，主要核心芯片采用EP1C12Q240C6；DSP开发板采用型号为SEED-DEC6416的嵌入式DSP控制模块系列，主要器件包括主频可达1 GHz的高性能32 bit定点DSP（TMS320C6416T），外扩有高速大容量存储器、标准USB 2.0控制模块、2路接口标准可切换的RS232/RS422/RS485通用异步接口、标准的外部存储器接口扩展总线和外设扩展端口，主要作用是进行复杂的数学运算，在本实验中主要根据设定的一阶循环均值算法程序对信号进行分类特征的提取、分类器决策函数值的计算以及中间结果的存储等。

实验中首先将一阶循环均值算法程序写入DSP，当射频信号发生器产生需要识别的各种VHF频段调制信号时，经过A/D采样得到一组离散值，将结果传入FPGA，DSP从FPGA中读取该组数据，按照设定的一阶循环均值算法对读取的离散值（每2 048个点）进行一次分类特征提取，并刻画该调制信号特点的分类器以实现对信号的调制识别。DSP识别出的调制方式信息通过USB接口传给PC，由PC显示识别结果。

6 结束语

通过一阶循环均值算法对VHF频段信号进行分析，实现对AM（含ASK）、FM（含FSK）、MFSK及其他调制信号（DSB、SSB、PSK、MPSK、QAM、MQAM）的调制分类识别，分类识别性能与调制阶数M、载波相位θ、时延t0、频偏Δf、信噪比SNR及观察时间间隙等有关，在其他因素不变的情况下，调制阶数越高、频偏越小、观察时间间隙越小，该算法的分类识别性能越差，仿真结果与理论分析非常接近，且分类识别性能较好，在信噪比大于-6 dB时，对VHF频段上述4类信号的识别率可达到98%以上。

1 Jefferson S,Mengchou Z.Real-time modulation classification based on maximum likelihood.IEEE Communications Letters,2008,35(12):132～140

2 Wong M L D,Nandi A K.Semi-blind algorithms for automatie classifieatic for digital modulation schemes.Digital Signal Processingls,2008(1):209～227

3 Oka I,Fossorier M P C.A general othogonal modulation model for software radios.IEEE Transactions on Communications,2009,54(10):7～12

4 Cernazanu-Glavan C,Holban S.A model for determining the number of negative examples used in training a MLP.Innovations in Computing Sciences and Software Engineering,2010(1):537～542

5 侯健,王华奎.一种基于星座图聚类的MQAM识别方法.无线电通信技术,2009(3)：35～38

6 位小记,谢红,郭慧.基于支持向量机的数字调制识别算法.电子设计工程,2011,35(6):89～91

7 王玉娥,张天骐,白娟等.基于循环自相关的OFDM调制识别方法.电视技术,2012,68(5)：44～48

8 张秀丽，李海清，李艳斌.基于谱域联合特征的信号调制类型识别.无线通信技术,2010,35(5):59～61

9 Avci E,Hanbay D,Varol A.An expert discrete wavelet adaptive network based fuzzy inference system for digital modulation recognition.Expert Systems with Applications,2007(3):582～589

10 Dobre O A,Abdi A,Bar-Ness Y,et al.Cyclostationarity-based modulation classification of linear digital modulations in flat fading channels.Wireless Personal Communications,2010,54(4):36～48

11 Ramkumar B.Automatic modulation classification for cognitive radios using cyclic feature detection.IEEE Circuits and Systems Magazine,2009,9(2):45～58

12 Qi Y,Peng T,Wang W B,et al.Cyclostationarity-based spectrum sensing for wideband cognitive radio.Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing,2009,1(1):52～63