基于QoS的超级节点模式网格调度研究*

潘善亮，黄 希，茅琴娇

（1.宁波大学信息科学与工程学院 宁波315211；2.西安交通大学电子与信息工程学院 西安710049）

1 引言

网格计算[1]环境下，有效的资源管理方案及资源调度算法对优化资源的使用和资源调度效率的提高有着十分重要的作用。近年来提出的基于超级节点模式（super-peer model）的网格资源管理模式[2]在集中式搜索与扩展性强的、具有负载平衡以及容错性的分布式搜索之间实现了平衡，并为位于不同区域的网格物理组织之间进行互联提供了一个很好的框架。因此，基于超级节点模式的网格计算在提出后便成为研究的热点。超级节点网络与传统的P2P网络相似，在传统P2P网络的基础上，把每一个P2P节点变为一个超级节点，每一个超级节点作为服务器与一系列的客户机相连。这些超级节点之间则采用P2P方式在更高层次上相互连接。面向服务的开放网格服务体系结构（OGSA）[3]和Web服务资源框架（WSRF）[4]为网格与P2P的集成提供了一个框架，使不同区域的服务器可以使用Web服务实现P2P互连。

目前，国内外学者对超级节点模式网格计算的研究主要集中在如下3个方面：

·资源的发现与定位；

·超级节点之间的拓扑连接协议与体系结构；

·超级节点的选择方法，如Carlo M等[5]对超级节点模式的网格以及层次式网格、分布式纯P2P模式网格进行了性能仿真、分析和对比，得出超级节点模式网格的优点，还讲述了超级节点模式如何实现多机构网格资源管理中进行的服务发现[2]；Kwan S K等[6]采用一种gossip协议交换超级节点之间的资源信息，大大提高了资源的发现效率；Peter M等人[7]针对个人计算机P2P网络提出了一个能自行组织和管理的超级节点网络；Yin L等人[8]利用经常在线的节点作为超级节点来管理那些经常离开的不稳定节点，这些稳定的节点之间构成DHT（distribute hash table）环；Pasquale C等人[9]提出了一个超级节点模式系统结构的网格，可以对庞大的数据量进行分析；Wu C C等人[10]提出了一种网格架构G2G以实现自治网格之间的互联；Sheng H Z等人[11]对超级节点的选择进行了研究，通过评估超级节点的计算能力，提出了一个超级节点的选择策略。

Petri网[12]具有并发、异步、动态等特点，已成为模拟和分析信息系统的有力工具，在资源调度中得到了广泛研究和应用，但还有一些问题值得探讨，如参考文献[13]中利用Petri网对超级节点模式的网格调度进行形式化建模与理论分析，将超级节点模式的网格任务、资源节点和时间限制映射到层次、颜色、时延Petri网，但所建立的模型只考虑了时间维度的服务属性，其调度对象是简单的不可分割的独立任务，没有考虑网格资源的动态性等机制。

目前Petri网调度建模机制在超级节点模式网格计算方面的应用研究还存在如下几个方面的不足。

·资源分配和任务调度策略大部分以系统为中心，只考虑了服务时间维度的服务属性参数，较少考虑面向用户QoS的要求（如截止时间、费用上限以及二者之间的权衡参数）和用户需求的多目标性，导致资源分配无效和不公平的情况发生。

·超级节点模式的网格调度是针对相互独立的不可分割的任务进行的，而网格任务通常是可以分解的复合任务，因此有必要建立复合任务的调度机制，以优化调度策略。

·没有考虑网格资源的动态性，当资源出现故障时对

重调度机制考虑不足。

本文重点研究面向用户QoS参数（时间、价格以及二者之间的权重）要求的超级节点模式网格复合任务调度算法，分析复合任务的调度过程，给出系统的最佳调度方案和重调度机制，对任务的调度过程进行价格时延Petri网形式化建模与理论分析，以验证算法的有效性，为系统性能评价提供依据。

2 超级节点模式的网格资源管理模型

本文讨论的超级节点模型是如图1所示的分层体系结构。

依据节点的非功能参数，把性能评估参数较高的节点（以下称为超级节点）作为上层管理，构成系统中的骨干层。每个超级节点作为服务器与一系列由不同组织管理的客户机一起构成一个传统的网格模式，而这些上层超级节点采用P2P通信方式构成一个大规模网格。每个超级节点控制着一组本地计算机资源的访问权限，代表着一个超级管理域，称为网格社区。一般地，当网格社区内的用户节点需要访问网格时，超级节点在它的管理域内以传统网格集中式搜索方式查找匹配的资源，如果没有找到，则通过P2P方式在其他超级节点之间进行查询[14，15]。由此，引入如下定义。

定义1 peer-to-peer grid={super-peer1,super-peer2,…,super-peern}，其中，super-peer1,super-peer2,…,super-peern是grid community1,grid community2,…,grid communityn所 对应的网格虚拟社区。

定义2 super-peeri={node1,node2,…,nodem}，其中node1,node2,…,nodem表示具有自主能力的主机或其他资源。

定义3 nodei=(IDi,IDsuper-peeri)表示节点的属性，IDi、IDsuper-peeri分别表示节点标识符和节点所在的超级节点网格社区标识符。

3 基于市场经济体制的超级节点模式网格复合任务调度算法

3.1 复合任务调度模型

在网格环境中进行资源管理和调度是个非常复杂的问题。在网格系统中，大量地理上分布的各种资源为不同的组织所拥有，这些组织具有不同的使用规则、计费模型、负荷能力和使用模型，资源拥有者和资源使用者各自具有不同的目标、目的、策略和需求，一些传统的资源管理和调度方式在网格系统中并不适用，而基于计算经济模型的网格任务调度方案是一个很好的解决方案。

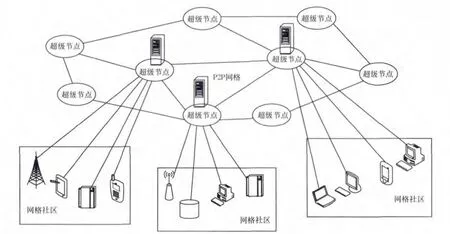
图1 网格计算超级节点模式的两层资源管理体系结构

基于市场经济的超级节点模式的网格复合任务调度模型如图2所示。在模型中，超级节点具有代理[16]功能，用户直接在本地计算机（源节点）提交任务，并规定任务的截止完成时间和费用上限以及时间和费用的偏好参数，任务被传输到本地超级节点，称这个超级节点为源超级节点。超级节点判断该任务是否能分解成子任务，如果能，则将任务分解成具有时间依赖关系的子任务集合，同时将时间、费用总要求分解，形成每个子任务的具体要求，并建立调度列表，然后按照调度列表选取并判断任务（子任务）能否在超级节点社区内提交它的资源节点并在截止时间内完成，如果能，则直接调度到它上面执行。

这里做出如下规定：

·每个资源节点在对应的超级节点处有一个用户账户，记录费用的使用状况，由超级节点负责管理；

·超级节点根据它所管理的资源利用状况给出对于具体任务的估计执行时间和费用；

·任务（子任务）在资源节点上执行时，不产生网格费用消耗。

相反地，当资源节点执行由其他节点（包括本网格社区内的其他资源节点和远程超级节点管理域内的资源节点）提交的任务（子任务）时，将收取一定的网格费用。因此，超级节点优先将任务（子任务）调度到提交它的资源节点上执行。若不行，则考虑将任务（子任务）调度到本地网格社区内满足用户要求的其他某一最优节点上执行。这一阶段，超级节点对其管理域内的本地资源节点采用集中式调度并进行内部资源节点之间的转账交易，这种优先本地任务策略能够减少网络阻塞。

图2 超级节点模式的网格任务调度模型

若任务（子任务）不能在超级节点社区内完成，超级节点将会与远程超级节点进行通信，以寻找符合要求的某一最优资源节点执行任务（子任务），并为之代付一定的费用。每个超级节点都有一张远程超级节点列表，并且可与它们交互，或存在一个中心目录来维护与每个远程超级节点相关的信息。这一阶段，超级节点之间采用分布式调度。

对于复合任务，以上过程不断地重复，直至调度列表中所有子任务都执行完毕。只有当子任务的所有前驱子任务都执行完毕后，该子任务才拥有被调度权。对于每一个任务（子任务），当执行它的资源节点发生故障时，携带错误报告的执行结果被传送到源超级节点，源超级节点进行必要的重调度，并撤销原来的相关交易。

基于以上调度模型，网格计算超级节点模式的超级节点代理框架如图3所示，其中GKD是global knowledge database的缩写，LKD是local knowledge database的缩写。

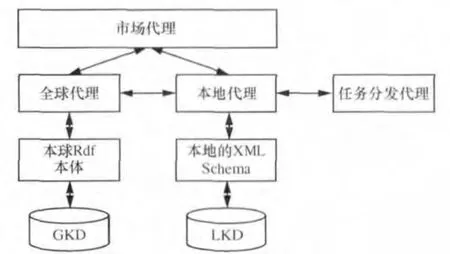
图3 超级节点代理的架构

超级节点代理架构包括4个分代理：任务分发代理（task-dividing agent）、本地代理 （local agent）、全球代理（global agent）、市场代理（market agent），各分代理的功能职责介绍如下。

·任务分发代理负责将本地资源节点上提交的网格应用分解成具有相互依赖关系的子任务集合（如果网格应用为元任务（meta task），则不用分解），建立调度列表，并将准备调度的任务交给本地代理。

·本地代理收到调度请求后，优先将任务（子任务）调度到源节点。如果不行，则在本地网格资源社区内查找相关的资源信息，若找到符合要求的资源，则联系市场代理为任务（子任务）选择最优的资源进行调度，并由市场代理进行交易管理。否则，把调度请求发送给全球代理。

·全球代理负责两方面的职责：一方面是将本地的XML Schema转换为全球的Rdf本体，存储在GKD中；另一方面是接收本地代理发送过来的调度请求，与其他超级节点代理中的全球代理进行交互，寻找合适的资源并联系市场代理，为任务（子任务）选择最优的资源进行调度，并由市场代理完成超级节点间的交易管理。全球代理准确地知道其他超级节点域的所有本体，并且含有相关本体的概要信息。

3.2 复合任务调度算法

3.2.1 基于时间和价格的多目标线性规划评价模型

定义如下参数：ti,j为任务（子任务）i在资源节点j上的估计执行时间，T为任务（子任务）的截止期限与到达时间之差，ci,j为任务 （子任务）i在资源节点j上的估计执行费用，C为任务（子任务）的费用上限，α+β=1,α≥0，β≥0。α、β为用户定义的时间和费用权重。

定义4在截止期限和费用上限均能满足的情况下，资源j对于任务（子任务）i的评价函数为：

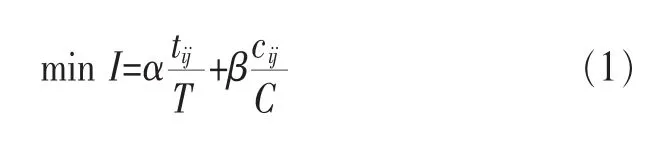
即超级节点将从符合要求的多个资源中选择使目标函数I最小的资源j作为任务（子任务）i的调度目标。

为了简化模型，假设超级节点模式的网络带宽足够宽，资源节点与超级节点以及超级节点与超级节点之间的通信、任务（子任务）以及结果的传输时延很小，相对于任务的执行时间可以忽略不计，所有任务或子任务均能在系统内找到合适的资源。

3.2.2 超级节点模式网格复合任务调度算法

算法具体如下。

Input：grid task GT

Output：mapping and assignment of grid tasks on nodes Begin

While GT comes from local grid community do

If GT can decompose

Else GT is called indivisible task；

For every grid task GTi(GTiis an sub-task or indivisible task)

If ExecutedTime(GTi,super-peers,nodej)≤DeadlineTime(GTi)//nodej是提交GTi的源资源节点

Then Allocate(GTi,super-peers,nodej)；

If an error occurs to nodej

Then SendResult0(GTi,super-peers)；

在PLC的理论教学中，我们通常会说PLC的功能很强大，在工业现场和许多场合都得到了广泛的应用。无论老师在课堂上讲得有多么精彩，学生对PLC的具体应用还是不清楚。如果在PLC的教学中运用虚拟仿真技术，通过计算机模拟实际的控制系统，那么效果将会大大提升。

//返回一个含有错误报告的执行结果，超级节点将会对GTi进行重调度

Else SendResult1(GTi,super-peers)；//返 回 正 常 的执行结果

Else if in super-peersexist nodek(k≠j)which meets the following two requirements:

ArrivalTime(GTi)+

ExecutedTime(GTi,super-peers,nodek)≤Deadline Time(GTi);//时间属性要求

ExecutedCost(GTi,super-peers,nodek)≤CostLimt(GTi)；//费用属性要求

Then for all nodekcalculate the function I;

Seek for the smallest I and the corresponding nodek′；

Allocate(GTi,super-peers,nodek′)；

If an error occurs to nodek′

Then SendResult0(GTi,super-peers)；

Else SendResult1(GTi,super-peers)；

Else Queuing(GTi,Peer-to-Peer Grid)；//先 将GTi插入队列中

Interact with other super-peers;

For every nodelin every(super-peers)which meets the following two requirements：

ArrivalTime(GTi)+

ExecutedTime(GTi,super-peers,nodel)≤Deadline Time(GTi)；

ExecutedCost(GTi,super-peers,nodel)≤CostLimt(GTi)；

Calculate the function I；

Seek for the smallest I and the corresponding super-peers、nodel′；

Send(GTi,super-peers);//将GTi发送到目标资源节点所属的超级节点End While

While GT comes from remote super-peers

Allocate(GT,super-peers,nodem)；//nodem指上面提到的nodel′

If an error occurs to

Then SendResult0(GT,super-peers,super-peerr)；

Else SendResult1(GT,super-peers,super-peerr)；

End While

End

4 网格调度的层次颜色、价格时延Petri网模型

Petri网是一个描述异步并发的图形工具，具有可达树、可达图、关联矩阵等多种分析方法，并且可以通过数学方法证明其正确性，本文把它同网格调度结合起来作为研究的工具。

4.1 价格时延Petri网以及用户应用定义

有关Petri网的基本概念、详细内容见参考文献[20]。本文给出价格时延Petri网的定义，具体如下。

定义5价格时延Petri网[21]CTPN=(PN,Γ,D,C)，其中：

·PN是Petri网，PN=（S,T,F）；

·Γ是一个集合，其元素（tj,τk）表示变迁tj实施的时刻为τk；

·D={dj/j=1,…，m},dj∈R+∪{0},表示完成 每个变迁tj所需要的时间，m为变迁的个数；

·C={cj/j=1,…，m},cj∈R+∪{0},表示完成每个变迁tj所需要的费用，m为变迁的个数。

用户可通过给定的d、c、τ定义对任务的QoS需求。用户复合任务进行分解后形成相互之间具有依赖关系的子任务集合，子任务之间存在诸如顺序、分支、循环、并行等关系。

定义6用户应用UA可以用类BNF表示为UA::=ε/X/T/T◇T/T茚T/T茌T/μT，其中：

·ε代表空任务；X代表一个任务常量，需要固定的时间和成本完成，这两个任务是为保证系统的完整性而引入的；

·T◇T代表两个任务顺序执行，总的执行时间为两

者执行时间之和，费用为两者执行费用之和；

·T茚T代表两个任务分支执行，一旦执行了其中的一个，则不执行另一个，相应的执行时间、费用等于被选中任务的执行时间、费用；

·T茌T代表两个任务并行执行，T1和T2应并行调度执行，总的执行时间取两者中执行时间最大的，而费用是两者之和；

·μT表示循环执行T共μ次，总的执行时间和费用为一次执行任务T对应值的μ倍。

4.2 网格任务调度的层次颜色、价格时延Petri网模型

定义7超级节点模式网格任务调度所对应的Petri网模型是一个层次颜色Petri网，HCPN=（Σ，P，S，T，F，C，G，E，I），其中：

·Σ={（rt,dt,dc,α,β）}∪{(et,ct)}∪{(ms,gt,gs)}是颜色的集合，rt、dt、dc分别是任务（子任务）的到达时间、截止期限、费用上限；α、β分别是用户规定的时间费用权重；et、ct是任务（子任务）在各资源节点上执行时所花费的时间和费用估计值；ms、gt、gs分别是资源的状态信息、任务（子任务）及其执行结果；

·P是子网的集合，P={super-peeri/i=1,2,…,n}，n是全局超级节点的个数，super-peeri是第i个超级节点所对应的子网；

·S是库所的集合，S={si1,si2/i=1,2,…,n}，n是全局超级节点的个数，si1是超级节点负责接收从远程超级节点发送过来的任务（子任务）与资源信息的单元，si2是超级节点向远程超级节点发送任务 （子任务）与资源信息的发送单元；

·T是变迁的集合，T={tijk/i,j=1,2,…,n,i≠j，k=1，2，3}，n是全局超级节点的个数，tijk表示第i个超级节点的发送单元向第j个超级节点的接收单元发送消息，此处每个变迁的时延、价格属性均为0，k=1，2，3分别表示发送本地资源节点的状态信息、任务（子任务）及其执行结果；

·F是弧的集合，F哿(P×S，S×P，S×T，T×S)；

·C是颜色函数，C∶S→∑；

·G是哨岗函数，G∶T→BoolExpression并且满足坌t∈T：Type(G(t))=Boolean∧Type(var(G(t))哿∑，其中，var(G(t))表示函数G(t)所含变量的集合；

·E为弧函数，E∶F→BoolExpression，并且满足坌f∈F，Type(E(f))=C(s)MS∧type(var(E(f))哿∑其 中，s为f连接的库所；

·I为初始化函数，I∶S→∑为每一个库所赋颜色值生成初始标识MS，即坌s∈S∶Type(I(s))=C(s)MS；

针对图1，为了简化模型，假定超级节点模式的网格由3个互连的超级节点组成，则对应的层次颜色Petri网（HCPN）模型如图4所示。

定义8第i个超级节点super-peeri所对应的子网为一个价格时延、颜色、增广Petri网。super-peeri=（Σ，S，T，F，W，M0，D，C），各变量的定义介绍如下：

·Σ={（rt,dt,dc,α,β）}∪{(et,ct)}∪{(ms,gt,gs)}是颜色的集合，rt、dt、dc分别是任务（子任务）的到达时间、截止期限、费用上限；α、β分别是用户规定的时间费用权重；et、ct是任务（子任务）在各资源节点上执行时所花费的时间和费用估计值；ms、gt、gs分别是资源的状态信息、任务（子任务）及其执行结果；

图4 超级节点模式网格调度全局层次颜色Petri网模型

·S是库所的集合，S={si/i=1,2,…,13}∪{(in,out)}，in对应超级节点的接收单元，out对应超级节点的发送单元；

·T是变迁的集合，T={tj/j=1,2,…,17}；

·F是弧的集合，W是弧的加权函数的集合，M0是初始标识；

·D∶T→R0是定义在变迁集T上的时延函数，D(t)=a表示变迁的发生需要a个单位时间来完成；

·C∶T→R0是定义在变迁集T上的价格函数，C(t)=b表示变迁的发生需要b个单位费用来完成。

super-peeri所对应的Petri网子网如图5所示，它是一个价格时延、颜色、增广Petri网。

对图5中对应的库所、变迁和抑制弧的说明见表1～表3。

5 系统性能

为了得到超级节点模式的网格任务最优调度方案，观察各任务（子任务）在执行过程中产生的时延和费用情况，对系统进行性能评价，构造和分析对应的Petri网可达任务图。

定义9层次颜色Petri网是超级节点模式网格调度对应的全局Petri网模型，HCPN的可达任务图(RTG)是一个有向图，表示为RTG(HCPN)=(V,E)，其中，V是由带标记的标识所组成的顶点集合，E是由带标记的连接标识的有向边所组成的边集合。借鉴参考文献[20]，RTG(HCPN)=(V,E)的构造算法如下。

图5 super-peeri所对应的价格时延、颜色、增广Petri网

表1 图5中的库所含义说明

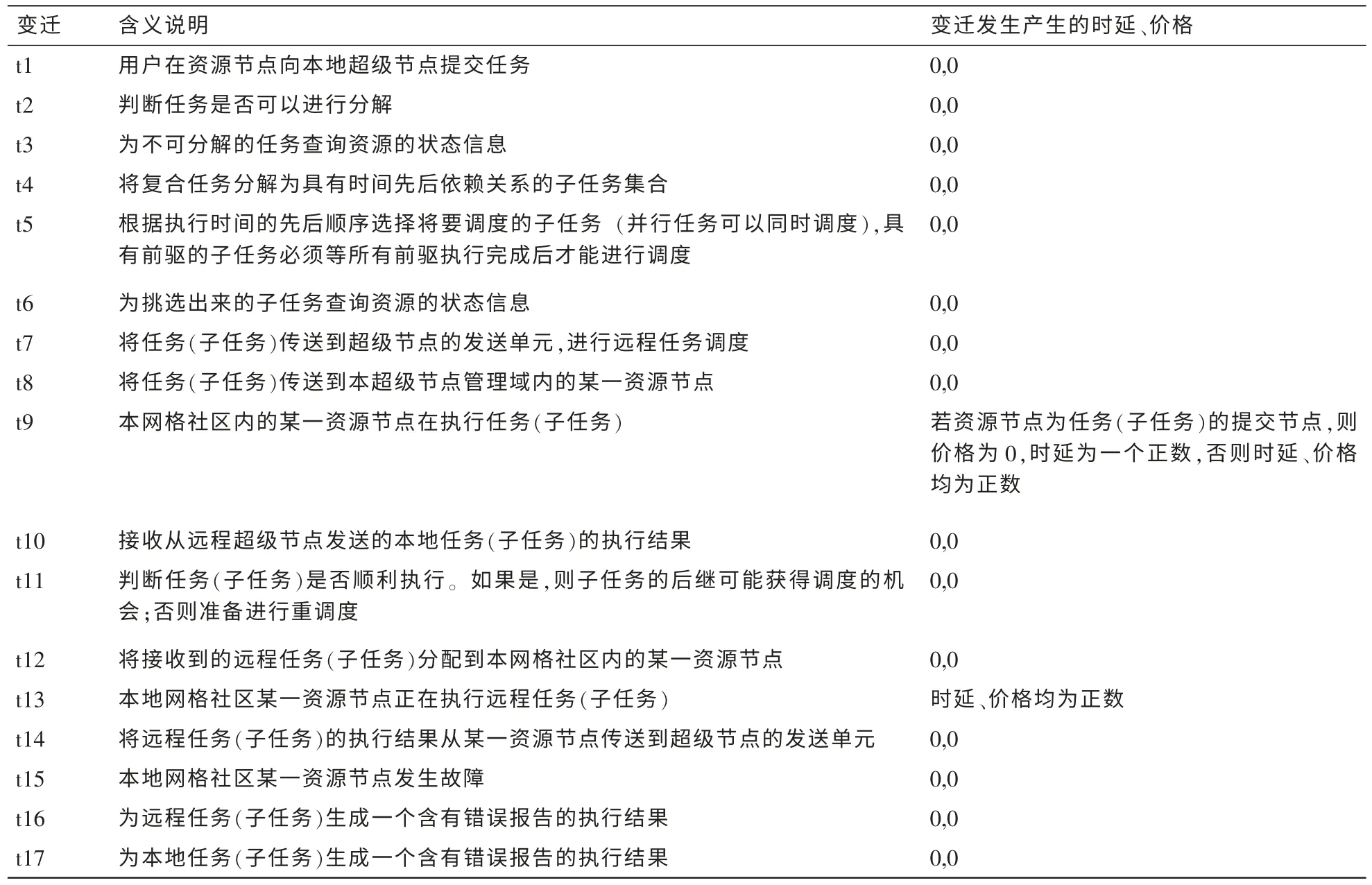
表2 图5中的变迁含义说明

表3 图5中的抑制弧含义说明

算法2计算可达任务图

输入：Petri网系统HCPN=。

输出：对于有界网系统，可达任务图RTG(HCPN)=(V,E)。

步骤1 RTG垂直分成m1+m2+…+mk+n个区域，其中n是超级节点的个数，mk是第k个超级节点中的客户机的个数。

步骤2初始化任务可达图RTG(HCPN)=（{M0，Φ}），M0标记为“新”。

步骤3 While在集合V中还存在标记为“新”的节点do

（1）从集合V中任意选择一个标记为“新”的节点M∈V

（2）For每一个在标识M下可以发生的变迁tj do

计算M′,使得M→tjM′；

If M′埸V

Then i V=V∪{M′};

ii If tj∈{t1,t2,t3,t4,t5,t6,t7,t11,t14,t16,tijk},则 将M′放在超级节点域内；

iii If tj∈{t8,t9,t10,t12,t13,t15,t17}则将M′放在超级节点内某一指定的资源节点域内。

E=E+{M,M′},并 将{M,M′}标 记 为tj/GTi,若tj∈{t9,t13}，则将tj附加标记[et,ec]，et、ec分别为GTi任务（子任务）在指定的资源节点上执行产生的时延和费用。

将M′标记为[a,b]，a表示当前的时刻，b表示目前任务执行到此累计消耗的费用。

（3）如果在标识M′下，原不可分解的任务执行完毕或者复合任务的所有子任务均已执行完毕，则将M′标记为“端点”；否则将M′标记为“新”。

（4）删除M的“新”，然后转到步骤3继续执行。

步骤4输出可达任务图RTG（HCPN）。

命题1设ne是RTG（HCPN）中“端点”的个数，则系统的吞吐量为ne。

证明 由算法2知，在RTG（HCPN）中，若为M′标记的“端点”，则表明有一个任务执行完毕，因此整个系统当前已完成的任务数，即系统的吞吐量为RTG（HCPN）中“端点”的个数。

命题2设etj为RTG（HCPN）的第k个资源节点区域中标注在执行变迁tj边上的时延分量，sek=∑etj，μ与s分别是序列{sek/=1,2,…，m1+m2+…+mk}的平均值与标准差，则离散系数v=s/μ可用来判断系统的负载平衡状态。

证明 由算法2知，RTG（HCPN）的第k个资源节点区域中标注在执行变迁tj边上的etj为某一任务(子任务)在第k个机器上的执行时间，而sek=∑etj即第k个机器执行时间之和。又因为离散系数v=s/μ用来度量序列{sek}中数据的离散程度，如果离散系数较小，说明各机器执行时间之和比较接近，因而系统就处于负载平衡状态，反之，系统就处于负载不平衡状态。因此，离散系数v=s/μ可用来判断系统的负载平衡状态。

命题3设Mk是RTG（HCPN）中的“端点”，ak、bk分别为Mk的时间、费用标识，则整个系统目前完成所有任务后所处的时刻为max{ak}，所消耗的总费用为∑bk。

证明 由算法2知，若Mk为RTG（HCPN）的“端点”，则表明某一个任务执行完毕，标注在Mk上的实数ak为当前时刻，即任务执行完毕的时刻，而系统完成所有任务后所处的时刻就是最后一个任务执行完毕的时刻，因此整个系统完成所有任务后所处的时刻为max{ak}；标注在Mk上的实数bk为当前任务执行完毕所耗费的累积费用，各复合任务之间相互独立，所以，系统目前完成所有任务后所消耗的总费用为∑bk。

6 实例分析

假设在如图6所示的一个超级节点模式的网格计算环境中，有两个相互独立的复合任务分别在节点1、节点3提交，它们的子任务结构如图7所示，其中节点1和节点2属于超级节点1所在的网格社区；节点3属于超级节点2所在的网格社区；节点4属于超级节点3所在的网格社区。

用户在提交任务时，可以定义其QoS参数要求，如完成截止时间、能承受的费用上限、时间与费用的权重。超级节点在接收到复合任务后，为了使调度方案的形成相对简单[21]，将复合任务的时间和价格QoS要求分解到每一个子任务，方便了调度方案的形成，大大减小了调度的复杂性。

图6 一个超级节点模式网格任务调度实例

图7 复合任务的子任务执行依赖关系结构

表4给出了这些任务（子任务）的到达时间、截止期限、费用上限、时间费用权重、任务（子任务）在各资源节点上的估计执行时间和估计执行费用。

根据这些参数和算法1、Petri网模型以及算法2，可以构造出该系统网格调度对应的Petri网的RTG（HCPN），如图8所示。

由表4及图8可得到如下分析结果。

网格任务GT1、GT2的子任务均不能完全在各自的提交节点上完成。对于任务GT1，其子任务GT1-1可以在截止时间内在提交它的节点1上执行完成，并不产生费用消耗。GT1-2、GT1-3虽然不能在提交它的资源节点1上按时完成，但是在截止时间和预算允许的情况下，它们都能在本地超级节点管理的资源节点2上执行。其中，GT1-2循环执行5次。对于任务GT2，其子任务GT2-1、GT2-2可以在截止时间内在提交它的节点3上执行完成，并不产生费用消耗。对于GT2-3，本地网格社区不能满足其QoS要求，超级节点2与超级节点1、3进行交互，发现满足其截止时间和费用上限要求的节点有节点1、节点2、节点4，此时超级节点2中的市场代理将计算每个符合要求的资源节点的评价函数：

通过对比可以看出，节点1的评价函数值最小，将GT2-3调度到超级节点1管理的节点1节点上执行。对于GT2-4，本地网格社区也不能满足其QoS要求，同时符合其截止时间和费用上限要求的资源节点只有超级节点3管理的节点4，故节点4就是其调度目标。同理，对于GT2-5，其调度目标也是节点4。

节点1执行所有任务所用时间之和se1=30+105=135，节点2执行所有任务所用时间之和se2=110+35=145，节点3执行所有任务所用时间之和se3=15+25=40，节点4执行所有任务所用时间之和se4=120+60=180。se1、se2、se3、se4的平均值为μ=125，标准差为s=51.84，离散系数v==0.41，由命题2知，系统目前的负载平衡状态一般，从执行时间分布上看，节点3的负载比较轻。

可达任务图有2个端点：M112、M215,系统的吞吐量为2。目前整个系统执行完所有任务后所处的时刻为max{175,245}=245，所消耗的总费用为120+160=280。

表4 网格任务（子任务）的时间、价格等QoS要求

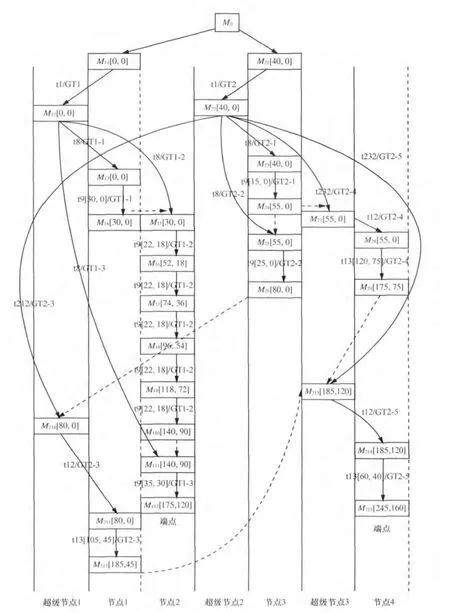
图8 网格调度Petri网模型的RTG（HCPN）

7 结束语

本文首先给出了一种超级节点模式的网格资源管理模型。针对此模型，引入市场经济机制，允许网格用户提出任务的完成截止期限、费用上限以及时间费用权重，将它们作为QoS参数。然后，给出对应的网格任务（复合任务）调度算法，并利用一种新的Petri网——价格时延Petri网对超级节点模式的网格任务调度进行建模。考虑到网格环境中资源是动态变化的，在调度算法及Petri网模型中增加相应的容错机制，当资源出现故障时，对任务进行重调度。最后，构建Petri网模型的可达任务图，通过一个例子，分析了具有顺序、并行或循环结构的复合任务的最佳调度方案、调度过程以及系统的吞吐量、负载平衡、调度时间、调度费用等重要特性。下一步的工作是进一步优化此模型，完善网格任务的调度算法，使各资源节点的时间负载特性能尽量保持平衡。

1 Foster I,Kesselman C.The Grid:Blueprint for New Computing Infrastructure.Morgan Kaufmann Publishers,San Francisco,CA,1999

2 Mastroianni C,Talia D,Verta O.A super-peer model for resource discovery services in large-scale grids.Future Generation Computer Systems,2005,21(10):1235～1248

3 Foster I,Kesselman C,Jeffrey M,et al.Grid services for distributed system integration.IEEE Computer,2002,35(6):37～46

4 The web services resource framework.http://www.globus.org/wsrf/

5 Mastroianni C,Talia D,Verta O.Designing an information system for grids:comparing hierarchical,decentralized P2P and super-peer models.Parallel Computing,2008(34):593～611

6 Kwan S K,Muppala J K.Resource discovery and scheduling in unstructured peer-to-peer desktop grids.Proceedings of the International Conference on Parallel Processing Workshops,San Diego,CA,2010:303～312

7 Merz P,Wolf S,Schwerdel D,et al.A self-organizing super-peer overlay with a Chord core for desktop grids.Proceedings of IWSOS 2008,Vienna,Austria,2008:23～34

8 Li Y,Huang X L,Ma F Y,et al.Building efficient super-peer overlay network for DHT systems.Proceedings of GCC 2005,Beijing,China,2005:787～798

9 Cozza P,Talia D.A Super-Peer Model for Multiple Job Submission on a Grid.Core GRID Technical Report Number TR-0067,2007

10 Wu C C,Chin J H,Lin Y S,et al.G2G:a meta-grid framework for the convergence of P2P and grids.Proceedings of GPC 2009,Geneva,Switzerland,2009

11 Zhao S H,Chen G L，Wu G X,et al.A strategy for selecting super-peer in P2P and grid based hybrid system.Proceedings of Edutainment 2008,Nanjing,China,2008:192～199

12 Colored J K.Petri Nets-Basic Concepts,Analysis Methods and Practical Use:Basic Concepts(2nd Edition).Springer-Verlag,Heidelberg,Berlin,1996

13 熊曾刚,杨扬,曾明.基于Petri网的两阶段网格任务调度模型与分析.通信学报,2009,30(8):69～77

14 Andrade,Brasileiro N,Cirne F,et al.Discouraging free riding in a peer-to-peer CPU-sharing grid.High Performance Distributed Computing,2004,12(3):129～137

15 熊曾刚,杨扬,刘丽等.网络资源管理的Grid和P2P集成方案及其关键技术分析.控制与决策,2008,23(1):1～7

16 Foster I,Jennings N R,Kesselman C.Brain meets brawn:why grid and agents need each other.Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems,New York,USA,July 2004

17 Xiong Z G,Yang Y,Zhang X M.Integrated agent and semantic P2P grid resource discovery model.Proceedings of Eighth ACIS International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing,IEEE Computer Society Press,Qingdao,China,2007

18 袁崇义.Petri网原理与应用.北京:电子工业出版社,2005

19 吴哲辉.Petri网导论.北京：机械工业出版社,2006

20 吉罗,瓦尔克.系统工程Petri网建模、验证与应用指南.北京:电子工业出版社,2005

21 刘卫东,宋佳兴,林闯.基于价格时间Petri网的网格计算应用模型及分析.电子学报,2005,33(8):1416～1420