基于等参变换的发动机负荷特性插值方法研究
2014-02-28朱江苏刚宪约
朱江苏,刚宪约,柴 山
(山东理工大学 交通与车辆工程学院,山东 淄博 255049)
0 引 言
在汽车设计阶段对整车的燃油经济性和排放性做出预测是非常有价值的,而准确处理、应用发动机的负荷特性数据是对整车燃油经济性和排放性进行模拟计算的基础。
目前国内外主要的计算方法是直接对发动机的负荷特性实验数据进行多项式拟合[1-3],这种方法存在一定的问题,不能准确的计算汽车的百公里油耗;另一种常用的计算方法是碳平衡油耗实验法[4-5],就是利用汽车排放的尾气来反求汽车的燃油消耗量[6],这种方法需要先进行汽车的排放实验,较复杂且操作困难。国内外常用的这些方法,存在一定的问题,都不够简单准确。
笔者以某种车型为例,利用发动机负荷特性的实验数据,建立了等参变换插值法的数学模型,得到了汽车在任意工况下的负荷特性;并利用外插法得到汽车在怠速和输出扭矩为0时单位时间内的燃油消耗率;通过对比等参变换插值法和多项式拟合法,进一步说明了本方法的有效性。
1 矩形域的双线性插值法
矩形域的等参坐标变换如图1,节点条件有4个,因此,最多可以确定4个待定系数,取以下双线性多项式作为汽车负荷特性插值函数模式[7]。
q(n,T)=c0+c1n+c2T+c3nT
(1)
式中:q为发动机负荷特性;n为发动机转速,r/min;T为发动机扭矩,N/m;c0,c1,c2,c3为待定系数。

图1 平面4节点矩形域Fig.1 Node rectangular domain of plane 4
它是具有完全一次项的非完全二次项,式(1)中右端的第4项是考虑到n和T方向的对称性而取的,而未选n2和T2项。
根据节点条件,在n=ni,T=Ti处有:
q(ni,Ti)=qi,i=1,2,3,4
(2)
将式(2)代入式(1)中,可以求出待定系数c0,c1,c2,c3,然后再代回式(1)中,经整理后得到:
q(n,T)=N1(n,T)q1+N2(n,T)q2+N3(n,T)q3+N4(n,T)q4
(3)
其中,

(4)
如采用无量纲坐标:
(5)
则式(1)最终可以写成:
(6)
2 非等间隔四边形域等参变换方法
由于在测量发动机的负荷特性实验数据时,很难使得发动机都处于转速不同扭矩相同的状态,因此负荷特性数据基本上是不规则四边形。对于几何形状不规则的四边形,通过等参单元坐标变换,可以转化为矩形。图2为任意四边形单元变换为矩形单元,其中:(n,T)为物理坐标系,(ξ,η)为基准坐标系。

图2 4节点四边形单元等参变换Fig.2 Isoparametric transformation of 4 nodal quadrilateral
对于4节点四边形的坐标变换,在n方向和T方向各有4个节点条件,如果用多项式来表示坐标变换的关系,则n和T方向上可以写出包含4个待定系数的多项式,即:

(7)
式中:(n,T)为任意点N*的物理坐标。
4节点四边形单元的4个节点的基准坐标为:P1(1,1),P2(-1,1),P3(-1,-1),P4(1,-1)。
将4个节点的基准坐标代入方程(7),可得:


(8)
根据式(7),可以解得:

(9)
式中:A=a1b3-a3b1;B=(4T-b0)a3-(4n-a0)b3+a1b2-a2b1;C=(4T-b0)a2-(4n-a0)b2。
利用式(8)和式(9)求得a2和ξ之后,若a2=0且ξ=0,则方程(7)的第1个式子将不再含有η,因此需要将ξ代入方程(7)的第2个式子,才能解出η;否则将ξ代入方程(7)的第1个式子。得到ξ和η之后,可以利用式(6)建立任意点的燃油消耗率与节点燃油消耗率之间的关系。
3 怠速工况的燃油消耗率
怠速工况时,认为发动机的转速为其最低的稳定转速,发动机的输出扭矩为0。当发动机万有特性实验数据以单位千瓦时为单位时,无法描述发动机在怠速和扭矩为0时的燃油消耗率,因为此时的万有特性值为无穷大。因此为了求得此时的燃油消耗率,需要进行处理。
1)将发动机在最低稳定转速时单位千瓦时的燃油消耗率b经式(10)转化成单位时间内的燃油消耗率q:
(10)
式中:P为发动机的实际输出功率;Ttq为发动机的实际输出扭矩。
2)运用外插法求发动机在怠速和输出扭矩为0时单位时间内的燃油消耗率。图3为某一款发动机在转速一定时,单位时间内的燃油消耗率与扭矩的变化关系,从图中可以看出,在低扭矩时,单位时间内的燃油消耗率与扭矩基本上是线性变化的。假设怠速时单位时间内的燃油消耗率与扭矩的关系如式(11):
q=k·Ttq+q0
(11)

图3 单位时间燃油消耗率与扭矩的关系曲线Fig.3 The unit time of fuel consumption vs torque
利用发动机在怠速时测量的数据点进行线性拟合,可以求得k和q0的值,令Ttq=0,就可以求得发动机在怠速和扭矩为0时单位时间内的燃油消耗率。
4 计算实例
某大型载货汽车,满载质量17 680 kg,配置247 kW的发动机,采用6+1挡变速器(各挡的传动比如表1)。根据公司提供的整车配置参数和发动机的外特性试验数据,对整车的燃油经济性进行了6个工况的仿真计算[8]。

表1 传动系传动比
对该车进行6个工况循环试验,试验参数见表2。
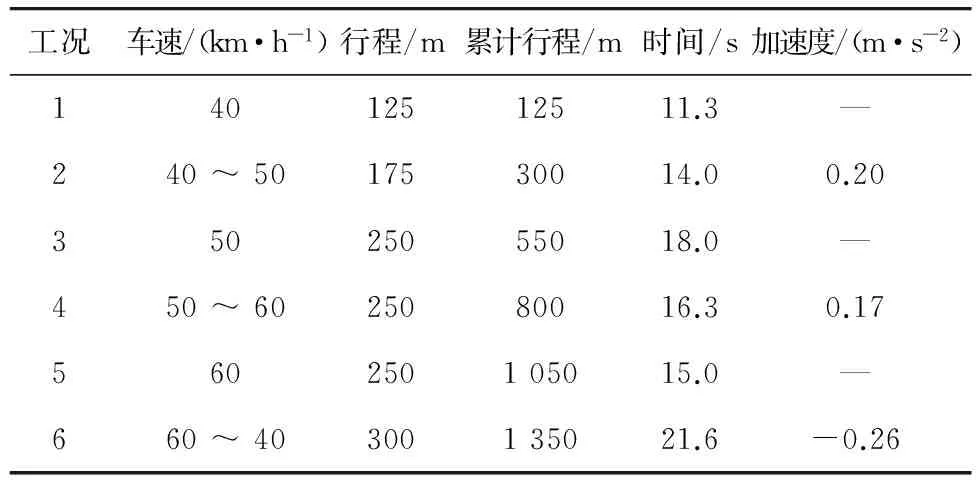
表2 货车6工况循环试验参数
按国家标准,汽车应采用最高挡进行试验,根据行驶车速、使用挡位和汽车行驶方程式可得到发动机转速和扭矩,采用等参变换插值法和多项式拟合法得到各工况的燃油消耗量,如表3。

表3 6个工况的燃油消耗量
注:*为采用单位时间内的燃油消耗率进行多项式拟合得到的各工况燃油消耗量;**为采用单位千瓦时的燃油消耗率进行多项式拟合得到的各工况燃油消耗量。
从表3可以看出,当采用等参变换插值法时,得到的各工况的燃油消耗量和百公里油耗,与单位时间内的燃油消耗率多项式拟合相差较小,但是与单位千瓦时的燃油消耗率多项式拟合相差较大。从而说明了本插值方法的可行性和有效性。
从表3的第6种工况(怠速工况)可以看出,怠速工况的燃油消耗量相差较大,说明了各计算方法在怠速工况计算燃油消耗率时存在较大的误差。而笔者提出的怠速工况单位时间内燃油消耗率的外插法经过了实验数据的验证,可以更加准确的得到怠速工况的燃油消耗率。
当采用单位时间内的燃油消耗率进行多项式拟合时,万有特性的拟合曲面如图4,利用拟合多项式得到在实验点上的计算值,根据计算值与实验值得到相对误差,拟合曲面,如图5。

图4 单位时间燃油消耗率万有特性曲面Fig.4 Universal characteristics surface of fuel consumption in the unit time

图5 单位时间燃油消耗率相对误差曲面Fig.5 Relative error surface of fuel consumption in the unit time
当采用单位千瓦时的燃油消耗率进行多项式拟合时,万有特性的拟合曲面如图6,利用同样的方法得到的相对误差曲面如图7。

图6 单位千瓦时燃油消耗率万有特性曲面Fig.6 Universal characteristics surface in the unit kW·h of fuel consumption

图7 单位千瓦时燃油消耗率相对误差曲面Fig.7 Relative error surface in the unit kW·h of fuel consumption
从图6可以看出,当采用单位时间燃油消耗率进行多项式拟合,拟合曲面较光滑,可以较为准确的得到各点的燃油消耗率值;而采用单位千瓦时燃油消耗率进行多项式拟合,准确性较差。从图5可以看出,当采用单位时间燃油消耗率时,相对误差较小,平均误差为0.32%,边界误差不超过5%;当采用单位千瓦时燃油消耗率时,相对误差较大,平均误差为2.71%,边界误差超过10%。
5 结 语
利用发动机负荷特性实验数据,建立了等参变换插值法的数学模型,得到了汽车在任意工况下的负荷特性;利用外插法得到汽车在怠速时单位时间内的燃油消耗率;最后通过对比等参变换插值法和多项式拟合法,说明了本方法的有效性。此方法也可以准确的计算汽车的排放性。
[1] 廖发良.汽车动力性与经济性模拟计算分析[J].公路与汽运,2010(4):10-13.
Liao Faliang.Automobile dynamic and economy simulation calculation and analysis [J].Highways & Automotive Application,2010(4):10-13.
[2] 关志伟,杨玲,施继红,等.基于MATLAB语言的发动机万有特性研究[J].吉林农业大学学报,2003,25(3):339-342.
Guan Zhiwei,Yang Ling,Shi Jihong,et al.Research of engine universal characteristics based on MATLAB[J].Journal of Jilin Agricultural University,2003,25(3):339-342.
[3] 詹樟松,杨正军,刘兴春.汽车动力传动系统参数优化设计和匹配研究[J].汽车技术,2007(3):17-20.
Yan Zhangsong,Yang Zhengxing,Liu Xingchun.Optimization design and match research of vehicle powertrain parameters [J].Automobile Technology,2007(3):17-20.
[4] 石则强,纪常伟,王伟,等.车辆燃料消耗量计算方法研究[J].车辆与动力技术,2010(4):19-24.
Shi Zeqiang,Ji Changwei,Wang Wei,et al.Study on calculating method of vehicle fuel consumption [J].Vehicle & Power Technology,2010(4):19-24.
[5] 文孝霞,杜子学,栾延龙.汽车动力传动系匹配研究[J].重庆交通学院学报,2006,25(1):138-141.
Wen Xiaoxia,Du Zixue,Luan Yanlong.Matching research of automobile’s engine and transmission [J].Journal of Chongqing Jiaotong University,2006,25(1):138-141.
[6] 宋传学,靳立强,彭彦宏.考虑排放约束的汽车动力传动系匹配[J].吉林大学学报:工学版,2006,36(4):506-509.
Song Chuanxue,Jin Liqiang,Peng Yanhong.Vehicle power train matching considering exhaust emission constraint [J].Journal of Jilin University;Engineering and Technology,2006,36(4):506-509.
[7] Li Hongyan,Gang Xianyue,Li Lijun.Automatic multi-node constrains algorithm and its application in vehicle structure analysis [J].International Journal of Computer Applications in Technology,2011,41(1/2):22-27.
[8] 韩越.汽车传动系统匹配优化方法研究与软件系统研制[D].淄博:山东理工大学,2010.
Han Yue.Research on Optimal Matching Method and Software Development of Autobile Powertrains [D].Zibo:Shandong University of Technology,2010.
