基于机构分析法的圬工拱桥病害产生机理研究

洪 华，刘山洪，马登阳

(重庆交通大学 土木建筑学院，重庆 400074)

近年来，国内外众多专家及学者针对圬工拱桥病害产生机理进行了深入的研究，得出了许多具有重大意义的结论和建议[1-4]。然而，现有许多针对圬工拱桥分析的理论，都是建立在线弹性理论基础之上的，对于出现空洞、风化、裂缝的圬工拱桥，也都是偏安全地通过线弹性理论验算来确定其病害状况，再得出其病害等级[5-10]。我国JTG H 11—2004《公路桥涵养护规范》即是根据线弹性理论和半概率理论的原则，在多家单位通力合作下完成的[6]。但是，笔者在对重庆市永川区桥梁进行普查时发现，很多圬工拱桥其主要承力部位(主拱圈)裂缝宽度实际上已经远远超出了JTG H 11—2004《公路桥涵养护规范》及《桥梁养护管理手册》的规定值，这些桥梁不仅没有出现垮塌的现象，而且还能正常通行车辆。

对拱桥这种主要承受弯压荷载的结构，当结构上某截面所承受的弯矩大于其塑性极限弯矩时，截面上会出现塑性区域进而产生塑性铰。截面出现塑性铰时，并不能使结构立即破坏，结构还能继续承受增加的荷载；当荷载继续增加时，先出现塑性铰的截面所承受的弯矩维持不变，产生转动，没有出现塑性铰的截面所承受的弯矩会继续增加，直至结构变成几何可变体系。笔者基于Heyman机构分析法、D.K.McNeely机构分析法及钱令希机构分析方法分别讨论圬工拱桥病害产生机理。

1 基于Heyman机构分析法的圬工拱桥病害产生机理分析

圬工拱桥在外荷载作用下，主拱圈自身的抵抗内力为了与外部荷载平衡，拱圈各截面会形成抵抗压力线。但抵抗压力线不会超出拱圈本身，当这条压力线与拱圈的上下边缘相交或相切时，该处将形成塑性铰，只发生变形，不增加内力。

自重、二期、汽车等外荷载作用下，圬工拱桥主拱圈弯矩如图1。

图1 主拱圈弯矩(单位：kN·m)

由图1可以推知，在过大外荷载作用下，主拱圈上最易形成塑性铰的位置位于主拱圈拱顶的底部和主拱圈拱脚的顶部，如图2。

图2 塑性铰形成位置Fig.2 Position of plastic hinge

图3为主拱圈拱顶及拱脚发生开裂形成铰的示意。

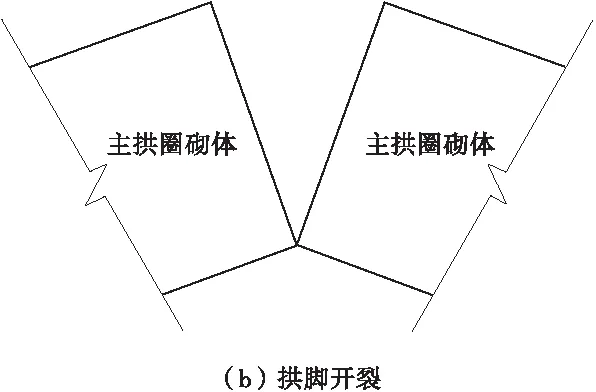
图3 主拱圈开裂形成的铰Fig.3 Formed hinge of the main arch cracking

对于一个构件来说，塑性铰个数过多将会导致结构变成机构，不能再承受外部荷载。所以对于无铰拱来说，塑性铰的个数不能超过3个，因为无铰拱是三次超静定结构，如果塑性铰个数超过3个，结构将变成机构。

因此，圬工拱桥的主拱圈(拱脚、拱顶)在长期外部荷载及本身风化、水蚀等现象作用下，易产生裂纹且裂纹会不断增长，直至发展成为贯穿主拱圈的横向裂缝，而变成第一个塑性铰的位置；拱圈内力相应调整，出现塑性铰的地方内力不再增加，其他地方内力增大，加速了其他地方裂纹的扩张；如此往复，直至主拱圈上产生多处裂纹，横向贯穿裂缝一旦超过3处，拱桥将发生垮塌。拱桥发生垮塌现象的临界状态是横向贯穿裂缝大于3处。

2 基于D.K.McNeely机构分析法的圬工拱桥病害产生机理分析

D.K.McNeely[2]对圬工拱桥按圬工材料进行了粗略的分类，将用大块的砌石材料(厚度≥500 mm)和很薄的砌缝材料(厚度≈5 mm)砌筑成的圬工拱桥定义为好质量的圬工拱桥；将用一般的砌石材料(厚度≤300 mm)和很厚的砌缝材料(厚度>30 mm)砌筑成的圬工拱桥定义为差质量的圬工拱桥。

对于质量高的圬工拱桥，完全可以利用三铰破坏机理进行分析；但对于质量差的圬工拱桥，应利用弹塑性分析方法确定主拱圈各处的实际抗弯刚度，进而判断主拱圈出现破坏的位置。

2.1 砌缝砂浆的应力应变关系〔式(1)〕

σ=a(ε)b

(1)

式中：σ为砂浆应力；ε为砂浆应变；a，b为与材料有关的系数。

2.2 应变曲率

砂浆砌体的抗弯刚度分为两种情况：①砌缝截面上没有出现拉应变，即砌缝全截面都能有效地参与工作；②砌缝截面因弯矩作用而出现拉应变，减小了砌缝截面的有效抗力高度。

临界状态应力应变的关系如图4。

图4 临界状态应力应变关系Fig.4 The critical state of stress-strain diagram

(2)

(3)

(4)

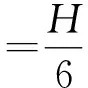
(5)

(6)

式(2)～式(6)中：T为截面轴向力；M为截面弯矩；e为轴向力偏心距；H为截面高度；其余符号意义同前。

所以，此处切缝截面的应变曲率为：

(7)

图5 截面出现拉应力时的应力应变关系Fig.5 Stress-strain relation when section tension stress appears

2.3 抗弯刚度

由式(7)可以看出，应变曲率随着压应力偏心距的增大而增大，当压应力的偏心距增大到甚至超过4/9H时，应变曲率将变得非常大，这说明压应力偏心距存在一个极限值emax，一旦偏心距超过这个极限值，该截面将转变成为塑性铰，仅起着铰的作用。当压应力偏心距很小的时候，截面上的应变曲率也非常小，对主拱圈的开裂应力影响也很小，这种情况下截面几乎不出现拉应力，若继续计算压应力偏心距将非常繁琐，所以此处采用二次曲线内插的办法计算压应力偏心距是合理的。通过压应力偏心距与应变曲率的关系，可以推导出砌缝砂浆的瞬间抗弯刚度：

(8)

因此，对于圬工拱桥的破坏应在圬工拱桥材料上进行分类。好材料的圬工拱桥，依据三铰破坏理论能确定其病害产生机理，但差材料的圬工拱桥就不能如此粗略的判断，而应该根据材料本身特性，确定材料实际抗弯刚度，通过实际抗弯刚度分析拱桥病害来源，从而得出其病害机理。换句话说，圬工拱桥的病害产生机理应根据圬工材料的不同而细分。

3 基于钱令希机构分析法的圬工拱桥病害产生机理分析

主拱圈上的砌体在外荷载作用下，其接触方式由原来的面接触慢慢变为点接触，同时接触点也慢慢向边缘移动，一旦接触点达到边缘后，它就不可能再向外移动(除非拱桥垮塌)，在后续过程中，若该截面再次承受外力，只会出现一种状况，即截面闭合；至此，该截面将不能再承受更大的外力，该处也就成为第一个塑性铰[3]。等到截面上出现3个以上的塑性铰时，该主拱圈将由三铰的静定结构变为机构，从而发生破坏。在给定分布以及数值的荷载作用下，拱桥主拱圈内会形成特定的压力线(图2)，压力线的形成服从平衡法。

由压力线在拱桥垮塌前不可能超出主拱圈边缘线，且以主拱圈截面形心轴为参考对象，可以得到压力线的约束位置：

(9)

式中：e为压力线相对约束位置；D为主拱圈最小厚度。

拱结构是一个弯压构件，其压力线的形成也受轴力、剪力及偏心距的影响。为了分析压力线形成过程及具体位置，通过力学简图(图6)进行分析，图6中左端脚反力的3个元素分别为V0，H0，e0，将主拱圈截面分成N个单元，每个单元划分出n个分段点，作用在其上的荷载有恒载Wn和活荷载Pn。

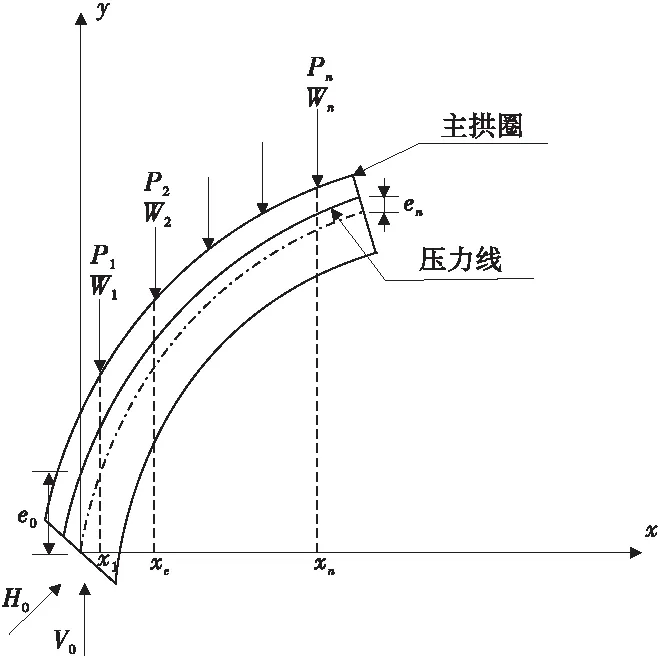
图6 力学计算简图Fig.6 Mechanical calculations schematic diagram

假设主拱圈压力线穿过截面n时，相对截面形心位置的值为en，由压力线上每一点对应的弯矩Wn=0，可以得到：

(10)

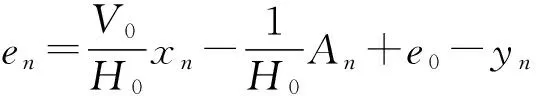
(11)

则，压力相对截面形心位置的值为：

en=β1xn-β2+β3-yn

(12)

式中：xn，yn为截面上分段点n处直角坐标。

由式(12)所算的压力线在圬工拱桥中穿行时，不能超出主拱圈砌体厚度的范围，这就进一步得出en的约束条件：

(13)

式中：φn为拱轴线竖向截面和法向截面的夹角。

最小主拱圈厚度可用数学规划法来确定，该分析方法是让主拱圈厚度按一定比例缩小，直到整个主拱圈因为塑性铰的数目超过3个而变成机构发生破坏，此时对应的主拱圈厚度就是所要求的最小厚度。在发生破坏之前，主拱圈内力所形成的压力线不断进行自适应，直至达到破坏的临界状态。主拱圈压力线的这种抵抗破坏的自适应能力，是来源于砌块与砌块之间传递内力的性质。

综上，主拱圈上出现裂缝的原因，是过大的外部荷载迫使主拱圈产生塑性铰，使得主拱圈开裂以释放自身约束，从而导致圬工拱桥主拱圈上出现裂缝。根据点接触假定、力平衡法以及极限状态可以明确确定主拱圈中压力线的位置，即可以定性地判断出最易出现塑性铰的位置，便于有针对性的进行加固，能节省大量人力、物力。

4 结 论

1)主拱圈在长期外部荷载及本身风化、水蚀等现象作用下，产生裂纹且裂纹不断增长，直至发展成为欲贯穿主拱圈的横向裂缝，而变成不能传递弯矩的塑性铰；一旦主拱圈上塑性铰个数超过3处，拱桥将发生垮塌，即三铰破坏机理。

2)差材料的圬工拱桥，应该根据材料本身特性，确定材料实际抗弯刚度，通过实际抗弯刚度分析拱桥病害来源，从而得出其病害机理。

3)实际工程中，应根据拱桥最不利荷载组合状态，确定主拱圈中压力线的位置，通过确定的压力线定性地判断出最易出现塑性铰的位置，进行有针对性的维修加固，即压力线定性分析机理。

4)基于机构分析法的研究可以得出，圬工拱桥病害产生的机理是：一个完整的构件，在外部荷载的作用下，会出现受力集中区，受力集中区的荷载一旦超过该区域的承载极限，将迫使该区域塑性化，此时，构件为避免被破坏掉，会通过产生病害的方式，形成塑性铰，稳定自身承受的能量。但是，一个构件允许出现的塑性铰个数是有限制的，一旦超过这个限制，构件将不再是几何不变体系，而是可变体系或瞬变体系，而这种体系不能再承力。

[1] 周建庭,刘思孟,李跃军.石拱桥加固改造技术[M].北京:人民交通出版社,2008:21-30.

Zhou Jianting,Liu Simeng,Li Yuejun.Stone Arch Bridge Retrofitting Technology [M].Beijing: China Communications Press,2008:21-30.

[2] McNeely D K,Archer G C,Smith K N.Structural analysis of old stone arch bridges[J].Canadian Journal of Civil Engineering,1989,16(6):789-797.

[3] 钱令希.赵州桥的承载能力分析[J].土木工程学报,1987(4):39-48.

Qian Lingxi.The analysis of Zhaozhou Bridge carrying capacity [J].China Civil Engineering Journal,1987(4):39-48.

[4] Harvey W J.Application of the mechanism analysis to masonry arches [J].Journal of Structural Engineering,1998,16 (5):77-84.

[5] 冉志红,屈俊童,和飞.桥梁结构损伤诊断的模式识别理论及其工程应用[M].北京:科学出版社,2011:3-15.

Ran Zhihong,Qu Juntong,He Fei.Methods and Application of Pattern Recognition Methodology in Damage Identification of Bridge Structures [M].Beijing:Science Press,2011:3-15.

[6] JTG H 11—2004 公路桥涵养护规范[S].北京:人民交通出版社,2004.

JTG H 11—2004 Code for Maintenance of Highway Bridge and Culvers [S].Beijing:China Communications Press,2004.

[7] Smith F W,Harvey W J,Vardy A E.Three-hinge analysis of masonry arches [J].Journal of Structural Engineer,1991,68(11):203-207.

[8] Boothby T E,Fanning P J.Loading rating of masonry arch bridge: refinements [J].Journal of Bridge Engineering,2004,9(3):304-307.

[9] Rong A.Structural analysis of an ancient arch bridge using modern technology [C].Nashville,Tennessee,USA:American Society of Civil Engineers,2004.

[10] Boothby T E,Dalal V A.Service load response of masonry arch bridges [J].Journal of Structural Engineering,1998,124(1):17-23.