扇区细分的永磁同步电机直接转矩控制系统建模与仿真
2014-02-28陈跃东
曹 龙,陈跃东,潘 帅
(安徽工程大学安徽省电气传动与控制重点实验室,安徽芜湖 241000)
永磁同步电机(简称PMSM)直接转矩控制(简称DTC)是根据当前磁链所在扇区,直接选取合适的电压矢量进行控制,该方法避免了旋转坐标变换,简化了控制结构,且转矩响应快,在高性能的交流伺服领域得到了广泛的应用[1].传统的DTC采用6扇区圆形磁链控制,系统的控制性能取决于对磁链位置的准确判断.但是当考虑定子电阻的影响时,传统DTC的电压矢量选择在扇区分界线附近时会出现错误,导致磁链在扇区分界线处的畸变,同时会引起电流的波动,带来一定的转矩脉动.针对以上问题,采取扇区细分的方法,将传统6扇区划分成12扇区,在MATLAB中对该控制方法进行建模并仿真.结果表明,采用扇区细分的控制方法能够获得更好的控制性能.
1 传统DTC系统
1.1 DTC的基本原理
面装式PMSM的电磁转矩方程为:

定子电压矢量方程为:

式中:ψs和ψr分别为定子、转子磁链矢量;Ls为定子电感;np为极对数,Rs为定子电阻;is为定子电流矢量;δsr为负载角[2].
定子电压矢量对定子磁链的作用如图1所示.每个基本电压矢量us都可分解为径向分量usr和切向分量usn.在us作用的时间内,依靠切向分量usn可以使ψs加速旋转,由于这段时间很短,加之电机的机械时间常数远大于其电气时间常数,所以转子的速度几乎来不及增加,因此负载角δsr就会增大,电磁转矩也就随之增大.反之,若在这段时间内使ψs反向旋转,则可减小负载角δsr,电磁转矩随之减小[2].负载角δsr可表示为:

图1 定子电压矢量对定子磁链矢量的作用图

切向分量usn与定子磁链ψs及其旋转速度ws的关系可表示为:

1.2 传统DTC电压矢量选择的缺陷
传统PMSM DTC将整个平面分为6个扇区S1~S6,如图2所示.先判断当前定子磁链所处扇区,再根据滞环比较器输出的磁链和转矩的控制信号Δψ、ΔT来选取合适的电压矢量进行控制.传统DTC的电压矢量选择表如表1所示.控制信号为1时,表示需要增加被控量;为0时,表示需要减小被控量;u1~u5为可供选择的6个基本电压矢量.

表1 传统DTC电压矢量选择表
在不考虑定子电阻压降的情况下,当定子磁链矢量ψs位于S1扇区时,电压矢量u2的作用是增加磁链和增加转矩,当定子磁链矢量ψs与S1扇区的下分界线重合时,u2和ψs刚好垂直,此时电压矢量u2对磁链幅值的增量为0.若考虑定子电阻时,式(2)改写为:

此时us作用Δt时间后,使定子磁链产生的增量为:
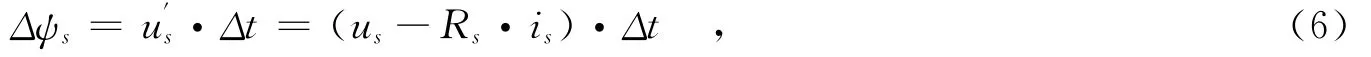
而us和的夹角为:

由图2可知,当考虑定子电阻的影响时,若选取电压矢量u2,其实际作用于定子磁链上的电压矢量相当于是u′2,与u2夹角为θ.假定当前定子磁链处于S1扇区的ψs2位置,若想要增加磁链并增加转矩,由表1可知,应选取电压矢量u2.如果ψs2与S1扇区下分界线的夹角θ1=θ时,u′2和ψs2刚好垂直;而如果θ1<θ,则此时u′2所起的作用是减小磁链、增加转矩,即u2所起的作用是减小磁链、增加转矩,这就导致了电压矢量选择的错误.同理,假定当前定子磁链位于S2扇区的ψs1位置,若想要减小磁链、减小转矩,由表1可知,应选取电压矢量u6.而当ψs1与S2扇区下分界线的夹角θ小于u′6和u6间的夹角θ时,u6所起的作用是增加磁链、减小转矩,此时的电压矢量选择也是错误的.在其他扇区对磁链分析得到的结论也相同.
在考虑定子电阻的影响时,传统的DTC在扇区分界线附近电压矢量的选择会出现错误,期望增加磁链幅值,但选择的电压矢量却会减小磁链幅值,这将导致定子磁链的非均匀变化,磁链轨迹不再是一个圆形,并会引起电流畸变,带来转矩脉动.

图2 6扇区划分图
2 扇区细分的DTC系统
2.1 12扇区细分和电压矢量选择表
针对以上分析,传统的DTC在扇区分界线附近,其电压矢量选择会出现错误.一种改进的方法是以传统6扇区分界线为中心再开辟6个扇区,将空间平面划分成12扇区[3],如图3所示.分析可得出12扇区的电压矢量选择表,如表2所示.

表2 12扇区电压矢量选择表
同样假定当前定子磁链处于ψs2位置,此时是位于S12扇区中,若想要增加磁链并增加转矩,由表2可知,应选取电压矢量u1.由图3可知,即使考虑定子电阻的影响,u1在整个S12扇区中所起的作用都是增加磁链、增加转矩.再假定当前定子磁链处于ψs1位置,此时是位于S2扇区中,若想要减小磁链、减小转矩,由表2可知,应选取电压矢量u5,而u5在整个S2扇区中所起的作用都是减小磁链、减小转矩,即使考虑定子电阻的影响,也不会出现电压矢量选择错误.
6扇区的电压矢量选择受定子电阻的影响,在扇区分界线附近会出现错误,而12扇区中选择的每个电压矢量在每个扇区中所起的作用都是唯一的,这就保证了磁链的均匀变化,使磁链尽可能的逼近圆形,并且在一定程度上减小了转矩的脉动.
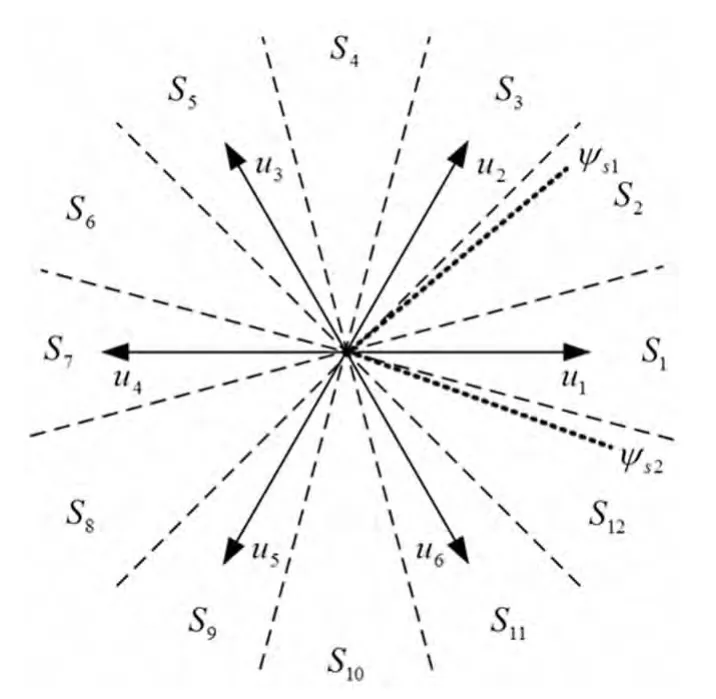
图3 12扇区划分图
2.2 扇区细分DTC的转矩控制性能
DTC的电磁转矩方程如(1)式所示,对(1)式求导:
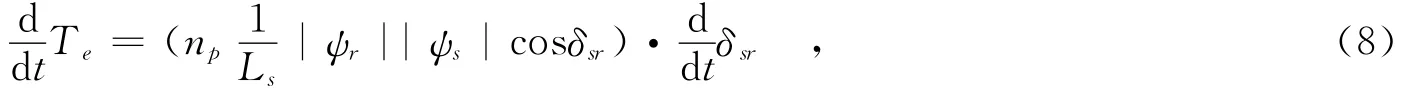
得到转矩Te随负载角δsr的变化关系:
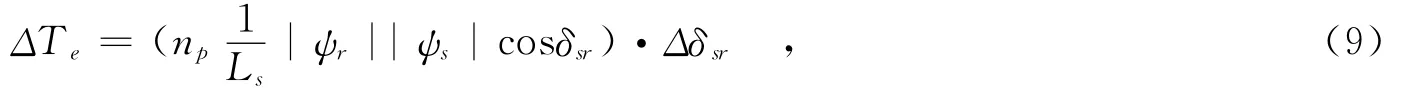
由式(4)变换得:

式中θuψ为电压矢量us和磁链矢量ψs的夹角.因为电机的机械时间常数远大于其电气时间常数,所以在us作用的这段时间内,假定转子的速度来不及变化,即负载角的完全由定子磁链转动的角度来决定[4].则结合式(3)得:

将式(11)带入式(9)中得:

假定6扇区和12扇区起始负载角相同,则转矩的变化只与θuψ这一个变量有关.不同电压矢量作用引起转矩的变化可用对的相对值来表示[5].令K=1,则不同的电压矢量作用所引起的转矩变化范围如表3所示.由表3可知,同样在S1扇区内,与传统6扇区相比,12扇区细分之后无论选择什么电压矢量作用,所引起的转矩变化范围都会相应减小,因此对转矩脉动起到一定抑制作用.
3 仿真与结果分析
在MATLAB中建立扇区细分的PMSM DTC系统仿真模型,如图4所示.仿真所选用的电机参数如表4所示.设定仿真时间为0.5 s,在0.25 s时,突加10 N·m负载.

表3 不同电压矢量作用引起的转矩变化
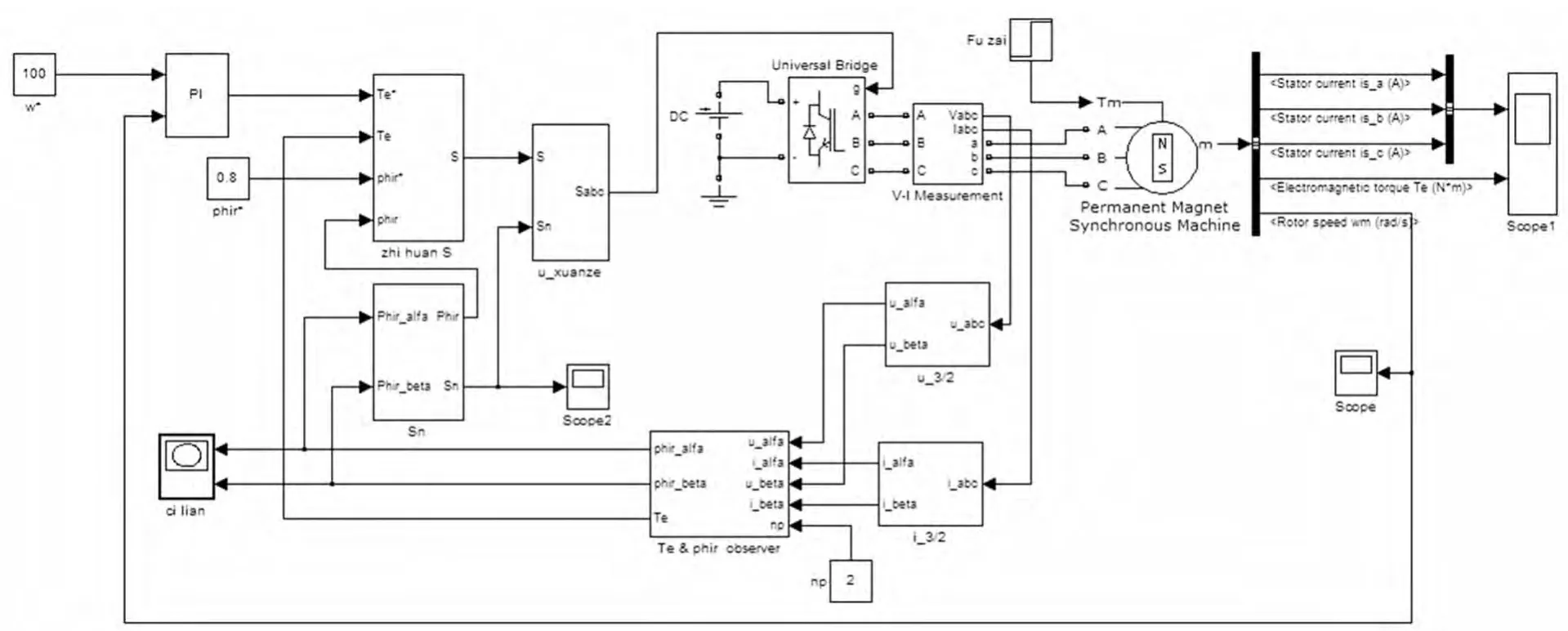
图4 扇区细分的PMSM DTC系统仿真模型

表4 仿真参数
相同条件下,传统DTC和扇区细分DTC仿真所得到的定子磁链轨迹、定子电流波形、转速响应波形和电磁转矩波形分别如图5、图6、图7、图8所示.由图5可知,传统DTC的定子磁链轨迹在每个扇区分界处的波动比较明显,而采用扇区细分之后的定子磁链已接近正圆形,改善了定子磁链的轨迹.为便于观察,定子电流仅截取0.14~0.2s的波形(见图6),传统DTC的电流波形有较大的脉动,采用扇区细分控制后,较好地抑制了这些脉动.由图7可知,在仿真开始后转速迅速上升至给定处达到平衡,0.25 s时突加负载,转速略微抖动后很快回到给定并继续保持稳定,且传统的DTC转速响应波形有略微的抖动,扇区细分之后抖动大部分已经消除.由图8对比可知,传统DTC系统的电磁转矩有很明显的脉动,而这些脉动在扇区细分的DTC系统中得到了抑制,说明扇区细分的DTC系统不仅保持了传统DTC系统的快速响应性和良好的鲁棒性,而且较好地抑制了转矩的脉动,控制性能更优.
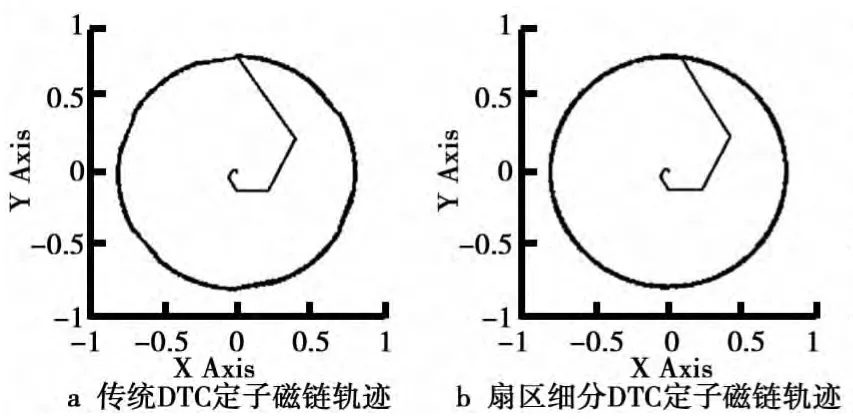
图5 定子磁链轨迹
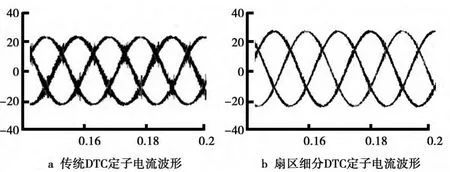
图6 定子电流波形

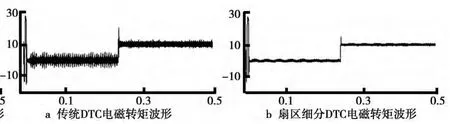
图8 电磁转矩波形
4 结论
分析了传统6扇区PMSM DTC系统的缺陷.当考虑定子电阻影响时,其电压矢量选择在扇区分界线附近会出现错误.研究了12扇区细分DTC系统的控制性能,改进了电压矢量选择表.在MATLAB中对两种控制方法进行建模并仿真.结果表明,采用扇区细分的控制方法能够较好地抑制转矩脉动,改善磁链轨迹,具有更好的控制性能.
[1] 阮毅,陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2009.
[2] 王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械工业出版社,2008.
[3] 孙驷洲.基于矢量细分的永磁同步电机直接转矩控制研究[J].电气传动,2010,40(6):16-19.
[4] 张崇巍,苑春明,张兴.中点电位平衡的三电平逆变器SVPWM简化算法及实现[J].电气传动,2008,38(11):37-41.
[5] 王建平.具有智能观测器的交流矢量控制系统[J].电气传动,1998(4):12-16.
