基于薄板理论的六维力传感器E型膜横向扭转振动分析

谢黎峰，许德章

（安徽工程大学机械与汽车工程学院，安徽芜湖 241000）

机器人六维力传感器是最重要的传感器之一，具备同时探测作用在末端执行器的3个力分量（Fx、Fy、Fz）和3个力矩分量（Mx、My、Mz）［1］.由于现有的六维力传感器6个通道之间存在干扰或噪声耦合，导致动态标定实验十分复杂和困难［2］.如刘正士和葛运建等，将单维力传感器弹性体简化成集中质量的单自由度二阶阻尼振动模型，利用脉冲激励法获得其动态特性［3］，但对于多维力系统动态特性提取尚无有效的实验手段.因此，通过理论分析寻找六维力传感器动态耦合特征具有十分重要的意义.对于电阻应变片式六维力传感器动态耦合特征的辨识，应着眼于其主要弹性体力学特征的研究［4］.双E型六维力传感器［5］是常见的应变片式六维力传感器之一，上、下E型膜是传感器最主要的弹性体结构，其动态特征决定着动态解耦矩阵C和传感器的动态输出.对六维力传感器弹性体动态特征的求解方法主要有实验建模、数值建模及解析建模［6］.由于动态标定实验过于复杂且现有实验手段难以达到传感器实际工作频率的带宽；而数值建模由于采用拟合逼近的方法，数值解本身与真实解之间存在一定误差；所以本文将采用解析建模的方法，基于弹性力学薄板振动理论，对圆环形薄板在动态力偶矩作用下的横向强迫振动问题提出一种新颖的解决方法，求解出测量主方向动载荷的各应变片的输出，并对结果进行数据处理，为六维力传感器动态解耦提供了理论和数据基础.

1 六维力传感器结构和受力分析

1.1 六维力传感器的结构

以中科院合肥智能研究所具有自主知识产权的超薄型双E型膜片六维力传感器为研究对象，其结构如图1所示.其中，矩形薄板1和上、下E型膜4、6分别为弹性体结构，电阻应变片粘贴在其表面，在受到动载荷作用时，会随之发生形变，经过桥路产生输出信号.上传力环2、中间传力环3、中心支柱5及底座7可看作刚体，在动载条件下不发生形变，用于传递外载荷.传感器的材料及尺寸参数如表1所示.

表1 六维力传感器的结构参数

1.2 六维力传感器的受力分析

动态标定实验中，给六维力传感器施加My方向的动载荷，即动态力偶矩，通常是在加载帽上沿x轴左右各施加一个大小相等、方向相反的动态激励力，如图2所示.这种受力状态下，测量Mz方向动载荷的矩形弹性体1，可以根据弹性力学矩形截面杆的扭转分析求解.由于中心支柱5看做刚体，因而下E型膜也受到一个动态力偶矩的作用，分析过程与上E型膜类似.所以本文以测量My主方向动载荷的上E型膜为例，重点分析圆环形薄板在非对称动载荷作用下的强迫振动问题.

将My方向动载荷作用下的上E型膜简化成一个内边界固定、外边界自由的圆环薄板，如图3所示.根据薄板的A、B两点分别作用一对大小qt1＝Ksinωt，方向相反的动态激励力，将这对剪力的作用效果等效为沿薄板圆周方向线性变化均布剪力，其中，A、B点剪力最大，C、D点剪力为0.在xoy平面内建立极坐标，以x轴为r轴，逆时针取φ.

图1 六维力传感器结构

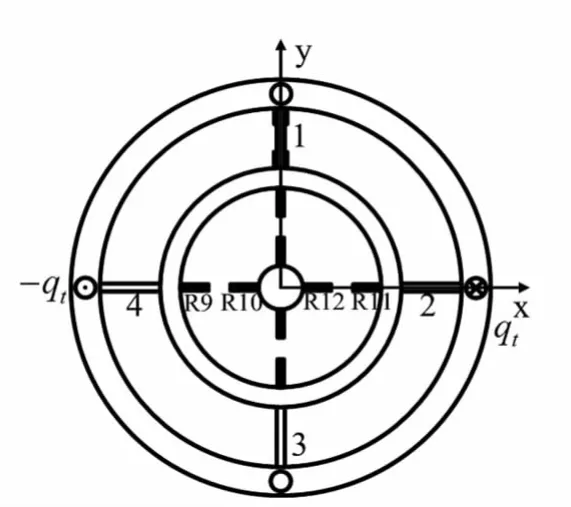
图2 六维力传感器俯视图

图3 上E型膜力学模型

2 六维力传感器横向扭转分析

2.1 圆环薄板非对称动载下扭转分析

根据极坐标系，将弹性力学薄板受迫振动微分方程改写为极坐标下圆形薄板受迫振动微分方程：

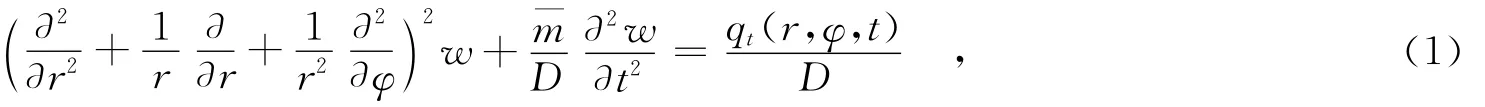
由于已经求解出圆环薄板自由振动的固有频率和振型函数［7］，将公式（1）中薄板所受的动力外载荷qt展开为振型函数的级数形式：

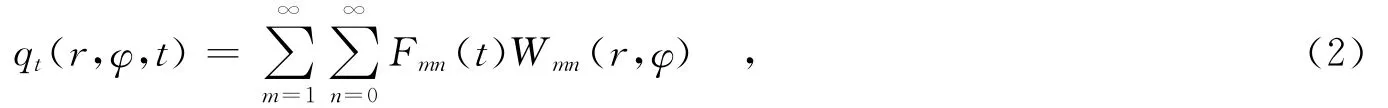
其中，m表示振型函数的阶数，n表示振型函数中Bessel函数的阶数.

把圆环薄板受迫振动微分方程（1）的解答也展开为振型函数级数的形式：

把（2）（3）两式代入式（1），比较两边系数，并化简得一常微分方程：

该常微分方程的解答可表示为：

其中τmn（t）是任意特解，系数Amn、Bmn由初始条件决定.将（5）式代入（3）式，得薄板在任意瞬时的挠度：

2.2 圆环薄板非对称动载下扭转振动算例

根据题设，在A、B两点分别作用一对大小qt1＝Ksinωt，按照受力分析，等效剪力沿圆周线性变化，求解出圆周上任意一点剪力的表达式：

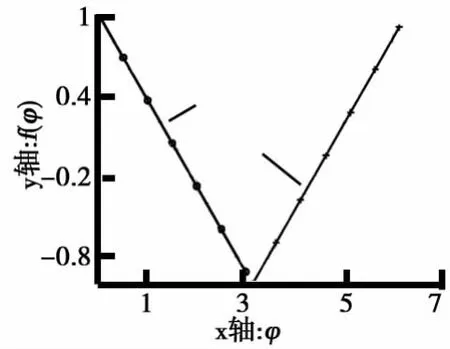
图4 f（φ）分段函数关系图

参照重三角级数展开公式，（2）式改写为广义力Fmn（t）的求解公式［7］：

按照式（8），代入剪力qt（r，φ，t）和振型函数Wmn（r，φ）.根据工程实际需要以及对计算量的控制，本文取前3阶振型函数，前2阶Bessel函数.求解出广义力如表2所示.

表2 各阶广义力值

结合零初始条件，即：

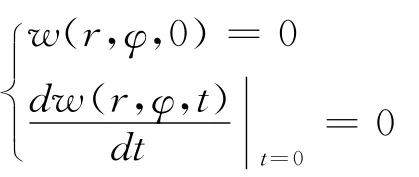
求解出系数Amn、Bmn.将系数及特解代入圆形薄板受迫振动微分方程的解（6）得：

由于本文研究的E型膜满足薄板小挠度弯曲理论的3个基本假设，根据弹性力学空间几何方程，推导出极坐标下得圆形薄板动态应变求解公式：

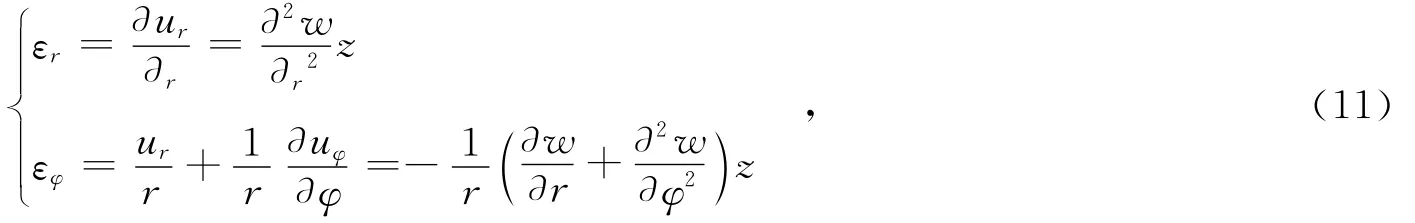
（1）由于应变片是贴在薄板的外表面，如图3所示，所以（11）式中z应取应变片贴附的薄板表面至中心面的距离：z＝h/2，薄板表面径向线应变：

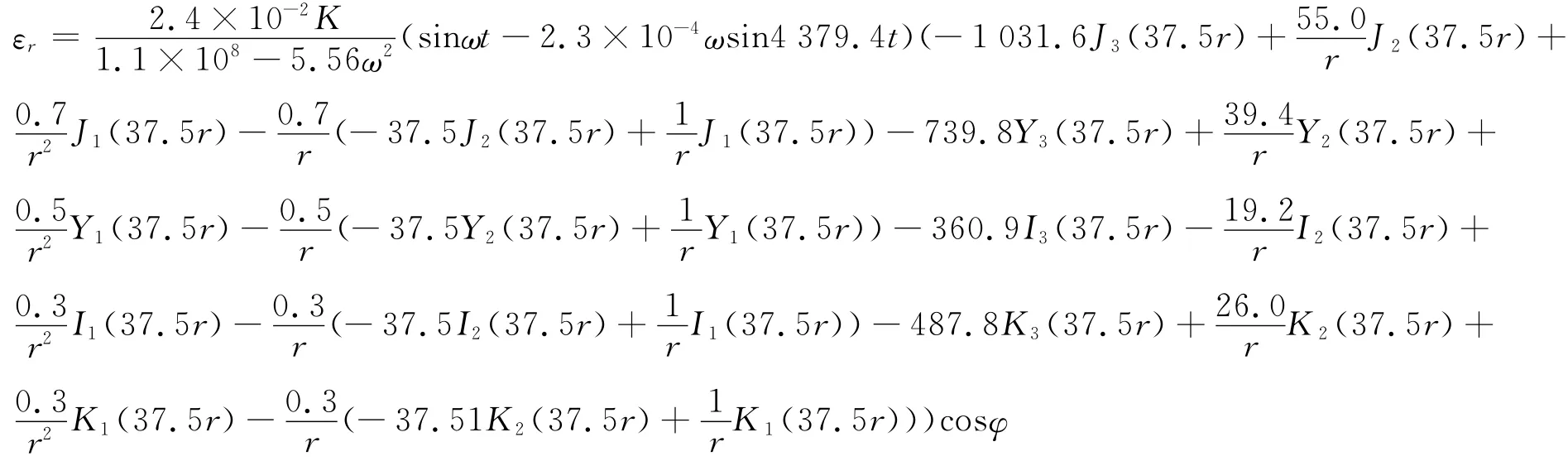
（2）同理，根据（11）中的第2式，求解出薄板表面周向线应变：

根据上述计算结果，对动态应变εr、εφ进行仿真.由求解出的εr、εφ可知，薄板表面动态应变εr、εφ的位置由r、φ决定.将表示激励力幅值大小的变量K取1，根据工程中机械手动态力带宽实际范围，选取激励频率2 KHz、8 KHz、10 KHz，仿真出上E型膜受迫振动沿r、φ两个方向线应变的四维空间切片图（图中方格内颜色的深浅代表此点应变的大小）如图5、图6所示.由图5、6可知，上E型膜径向线应变主要集中在粘贴应变片的轴线（即π、2π处）上，且在圆环板的内边界附近值较大，沿坐标轴r向外边界方向逐渐减小.周向应变在整个圆环板面都有分布，且分布较均匀.对动态应变εr、εφ进行矢量合成得合应变ε.ε中应变片的位置同样只由变量r、φ决定，代入各位置参数（各电阻应变片取中心点位置）得4应变片的应变（见表3）.

图5 上E型膜径向动态应变仿真

图6 上E型膜周向动态应变仿真

如图2所示，测量My方向动载荷的是粘贴在上E型膜的R9、R10、R11、R124片电阻应变片，构成了惠斯通电桥，R9与R11，R10与R12分别置于相对应桥臂上.根据My方向动载荷作用时，膜片变形、应变与受力关系［8］，推导出My方向动载荷作用下传感器的应变输出为：

将表3中的各参数带入式（12），得My方向动载荷作用下传感器的应变输出的具体表达式：

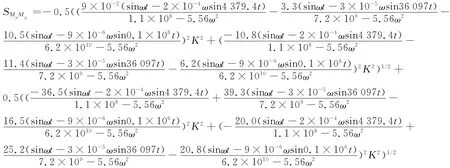
SMyMy就是My方向动载荷作用时，主方向通道动态输出的解析解.根据六维力传感器的动态标定公式可得所以上式求解出了SMyMy就等同于求解出动态耦合矩阵中的元素KMyMy.

表3 My方向动载下My方向电阻应变片输出

3 结论

基于弹性力学薄板强迫振动理论，对双E型六维力传感器的主要弹性体上E型膜进行分析，建立圆环薄板的力学模型，将外加非对称动载荷等效成薄板边界处线性变化的剪力，求解出圆环薄板表面任意位置横向强迫振动的应变.并仿真了动态应变的四维空间切片图，直观地揭示了弹性体在非对称动载下表面响应的分布.同时，基于电阻应变片的位置，对动态应变进行数据处理.动态输出的解析解为六维力传感器动态解耦算法研究在My主方向上提供了数据基础；从力学角度揭示了六维力传感器E型膜的动态特性，为其他方向动载荷作用时，E型膜的耦合输出研究提供了理论依据.

［1］ Wang Z J，Yao J T，Xu Y D，et al.Hyperstatic analysis of a fully pre－stressed six－axis force/torque sensor［J］.Mechanism and Machine Theory，2012（57）：84－94.

［2］ Song A G，Wu J，Li J Q，et al.A novel four degree－of－freedom wrist force/torque sensor with low coupled interference［C］//Proc.IEEE/RSJ Int.Conf.on Intelligent Robots and Systems，Beijing，China：Intelligent Robot and Systems，2006，4 423－4 428.

［3］ Liu Z S，Wang Y，Chen E W，et al.A method for measuring dynamic performance index of robots multi－axis wrist force sensor［C］//Proc.IEEE Int.Conf.on Information Acquisition，Hong Kong and Macau，China：Information Acquisition，2005：170－176.

［4］ Liang Q K，Zhang D，Song Q J，et al.Design and fabrication of a six－dimensional wrist force/torque sensor based on E－type membranes compared to cross beams［J］.Measurement，2010（43）：1 702－1 719.

［5］ 梁桥康，宋全军，葛运建.一种新型结构机器人的四维指力传感器设计［J］.中南大学学报：自然科学版，2009，40（1）：115－120.

［6］ 干方建，刘正士，任传胜，等.一种应变式六维力传感器的动态设计［J］.中国机械工程，2007，18（8）：967－970.

［7］ 汪志红.电阻应变片式六维力传感器弹性体力学特性的研究［D］.芜湖：安徽工程大学，2013.

［8］ 杨卫超，余永，邓小红，等.一种基于双E型膜片的微小六维力传感器的设计［J］.传感技术学报，2008，21（7）：1 137－1 142.

［9］ 徐芝纶.弹性力学（下册）［M］.北京：高等教育出版社，2006.