交变隐式时域有限差分法的媒质吸收薄层设计

张玉贤，郑宏兴，计雷雷

（天津职业技术师范大学天线与微波技术研究所，天津 300222）

交变隐式时域有限差分法的媒质吸收薄层设计

张玉贤，郑宏兴，计雷雷

（天津职业技术师范大学天线与微波技术研究所，天津 300222）

为了解决交变隐式时域有限差分法（ADI-FDTD）的截断边界问题，设计了一种媒质吸收薄层铺设在截断边界上，通过给定ADI-FDTD算法基本迭代形式，证明了媒质表面满足阻抗条件时可实现无反射条件。在一维和二维ADI-FDTD计算实例中发现，在这种媒质吸收薄层上电磁波能被很好地吸收，达到无反射的效果。

交变隐式时域有限管分法；媒质吸收薄层；无反射条件

时域有限差分法[1]（FDTD）在计算电磁学领域中是一种非常有效的算法，在微波电路、天线设计、电磁散射模拟以及电磁兼容问题上得到了广泛的应用。但对于传统FDTD方法而言，其运行过程中需要满足Courant稳定性条件。1999年，Namiki[2]提出了交替隐式差分格式（ADI）的FDTD算法，并验证了该算法不受制于时间分割[3]。在精细结构问题上，人们往往采用ADI-FDTD法[4-5]，但是在截断边界上需要比较复杂的算法来处理问题。本文设计一种媒质吸收薄层[6-7]，达到阻抗匹配条件[8-10]时，铺设于ADI-FDTD计算区域的周围，并通过数值计算来验证其吸收电磁波的有效性。

1 ADI-FDTD算法基本迭代形式

根据电磁现象的普遍规律，在无源空间中电磁波的传播取决于麦克斯韦方程组：

通过对空间算符▽中的变量进行离散后，采取交替迭代处理，并投影到一维空间上，得到一维ADI-FDTD差分格式为如下2个过程。

过程一 时间步n→n+1/2

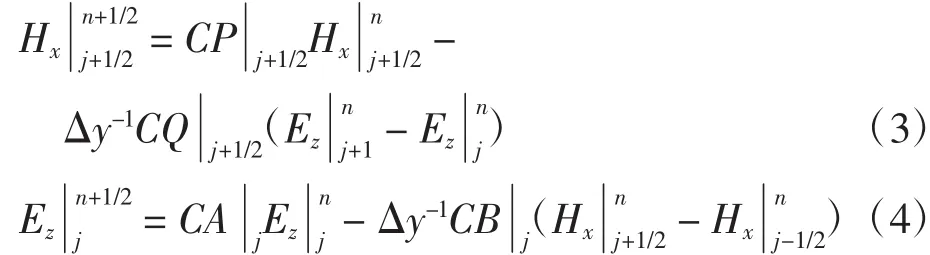
过程二 时间步n+1/2→n+1

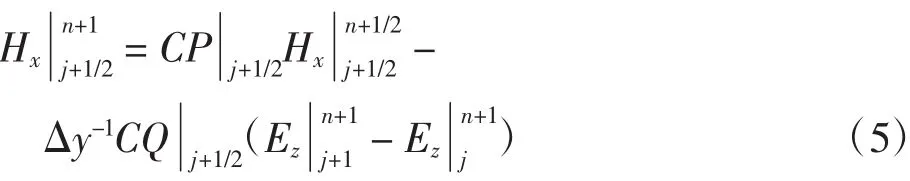
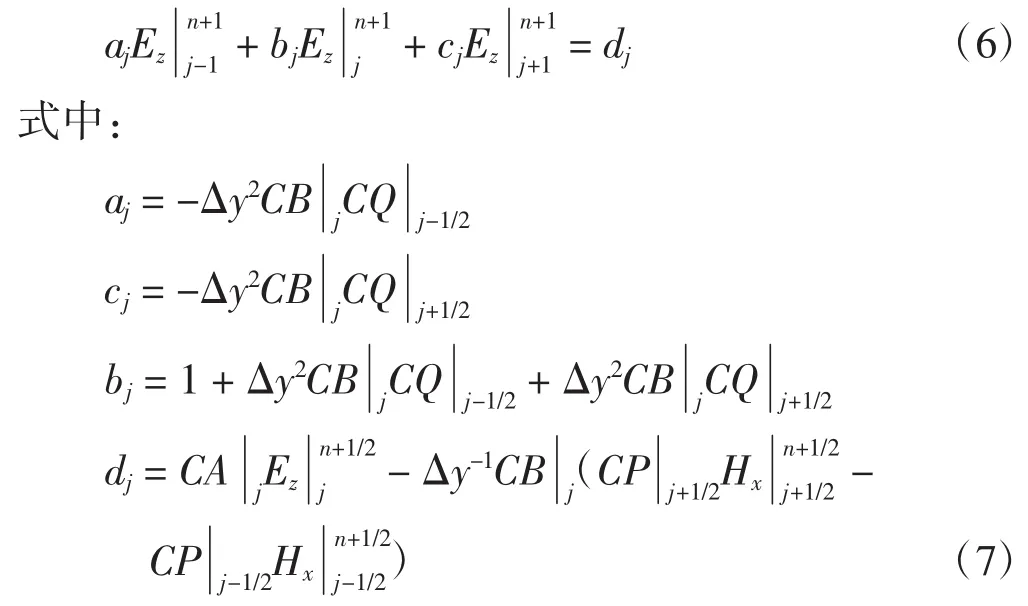
在过程二中，Ez为隐式变量，需通过求解三对角方程才可求解，称为隐式迭代过程。对于Hx在一维ADI-FDTD的2个过程中均为显式迭代过程。通过对（1）和（2）变换的同样过程，亦得到二维TMz下的ADI-FDTD迭代格式2个过程：

过程一 时间步n→n+1/2

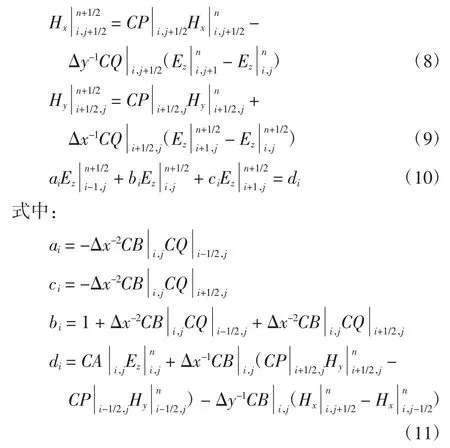
过程二 时间步n+1/2→n+1

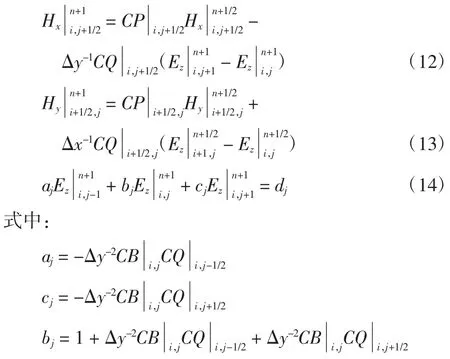
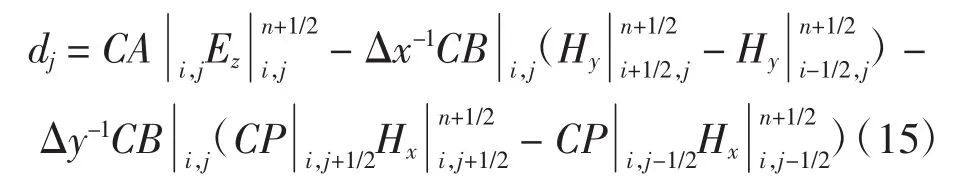
在二维ADI-FDTD中，Ez一直处于隐式迭代过程，而Hx和Hy均为显式迭代过程，并可实现无条件稳定。三维ADI-FDTD的求解过程如同上述步骤一样。

通过ADI-FDTD的迭代式，进行编程后，从而描述出空间中的电磁分布过程。经过数值验证后，发现ADIFDTD对精细结构的仿真有明显的优势，因此在其截断边界上设置一种媒质吸收薄层，可起到无反射条件。

2 媒质表面无反射条件推导

媒质表面电磁分布情况如图1所示。

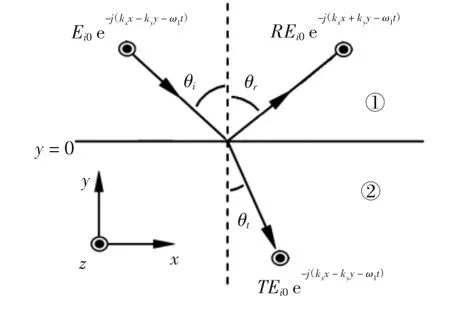
图1 媒质表面的电磁分布情况

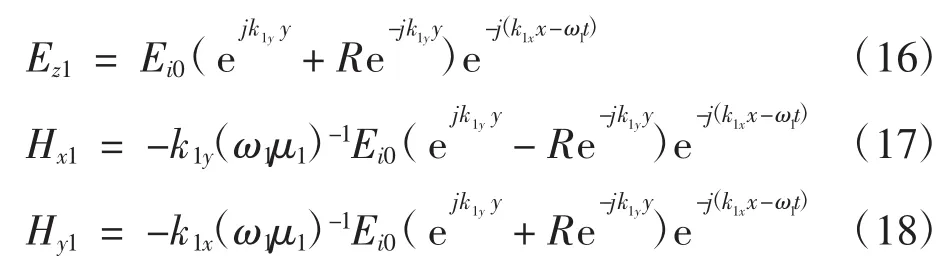
区域②的电磁场分布为：

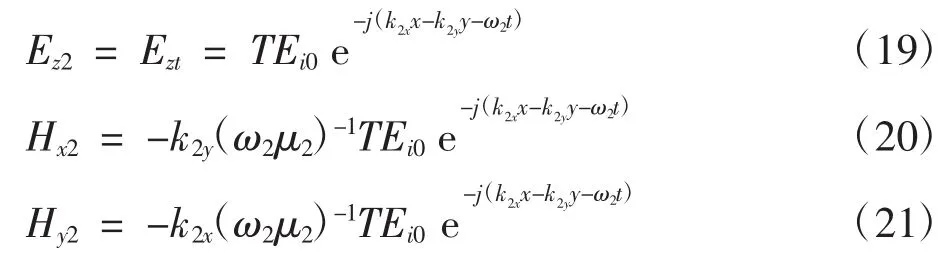
由电磁场的边界条件中切向连续的性质得到：

通过行列式方法求解上述方程，可得：

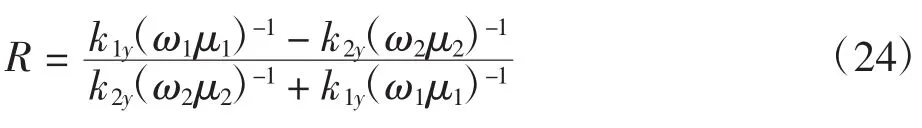
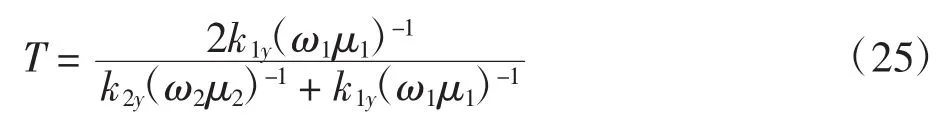
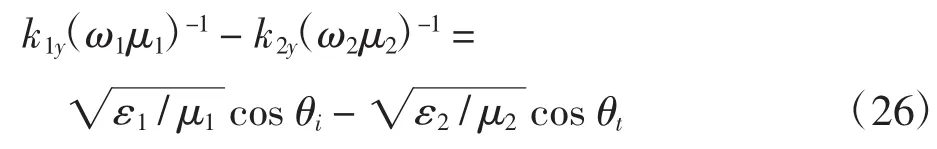
若考虑区域①的媒质为真空，区域②的媒质为有耗媒质，那么令ε2=Cε1，μ2=Cμ1，ε1=C′μ1，其中C、C′均为常数，则有：

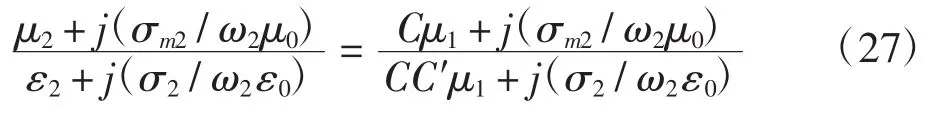
此时相应的反射系数为：

在光学理论中已验证了在阻抗匹配条件下入射角与折射角是相等的。在电磁场数值计算中，一般采取精细网格的切分手段便可在不同入射角下实现θi=θt。

3 数值结果验证

3.1 一维ADI-FDTD算例

通过上面的分析，不妨令ADI-FDTD算法中采用CFLN=2，选取满足式（28）的数据，设置媒质吸收薄层的电导率为σ2=0.828 3/λb，其中λb为基准波长，通过选取不同的λb，求解出不同的相对介电常数εr的值，如图2所示。

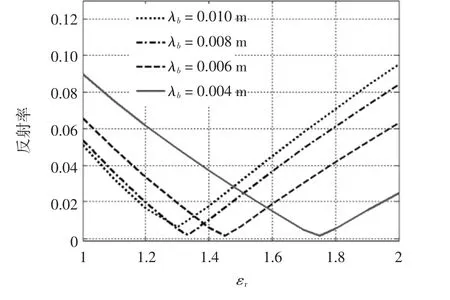
图2 在不同λb下选取的不同相对介电常数εr所对应的反射率曲线

由图2分析得到，当λb越小时，相对介电常数εr需要越大，才能取得最小反射率，因此这种媒质的设置在一维ADI-FDTD中是可行的。设置高斯脉冲形式作为电场上的源：

式中：t0=2×10-10。设置FDTD网格大小为Δx=2 mm，电磁波的传播过程如图3所示。

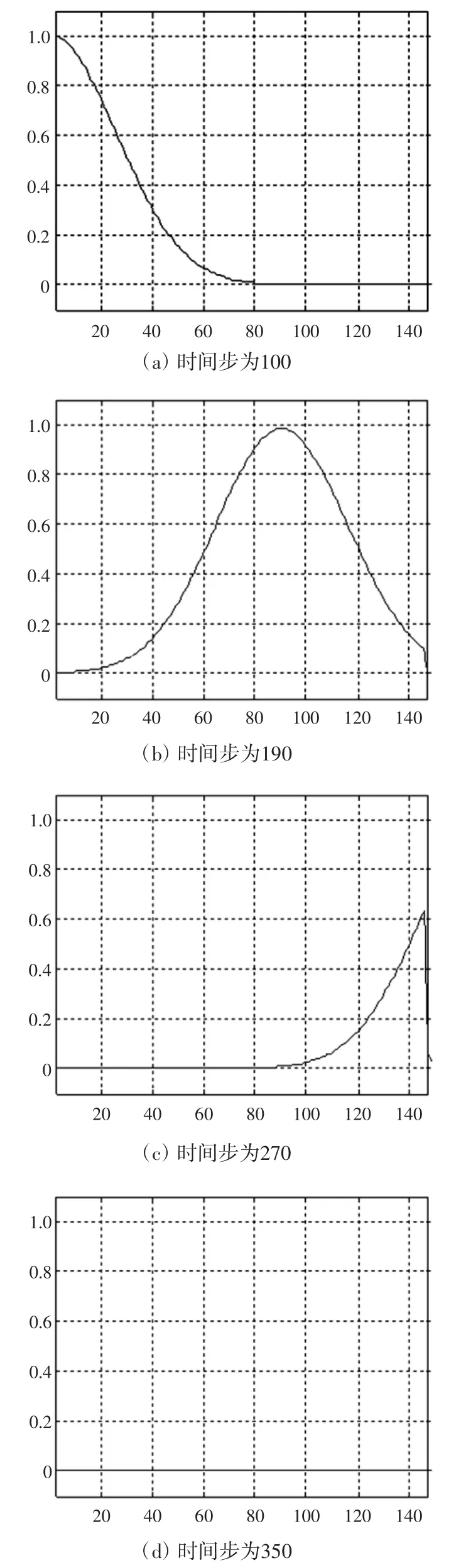
图3 高斯脉冲在媒质吸收薄层下吸收过程

经过多次数值实验，发现只需4～5个网格便可吸收99.85%的电磁能量，相对应的反射系数最低为0.001 5，即反射误差可达到-80 dB以上。

3.2 二维ADI-FDTD算例

按照上述的参数设定，可得到在二维ADI-FDTD下的结果。设置Δy=Δx，计算区域选定为（180Δx）2，在截断边界周围设置一层媒质吸收薄层，引入正弦点源，分别设定点源位置为（90，90）与（60，60），如图4所示。显然，图4（a）和（b）中同心圆的结果表明，上述媒质薄层在满足阻抗匹配条件下，寻找到适当的基准波长λb和相对介电常数εr时，便可在截断边界上实现有效的电磁波吸收。

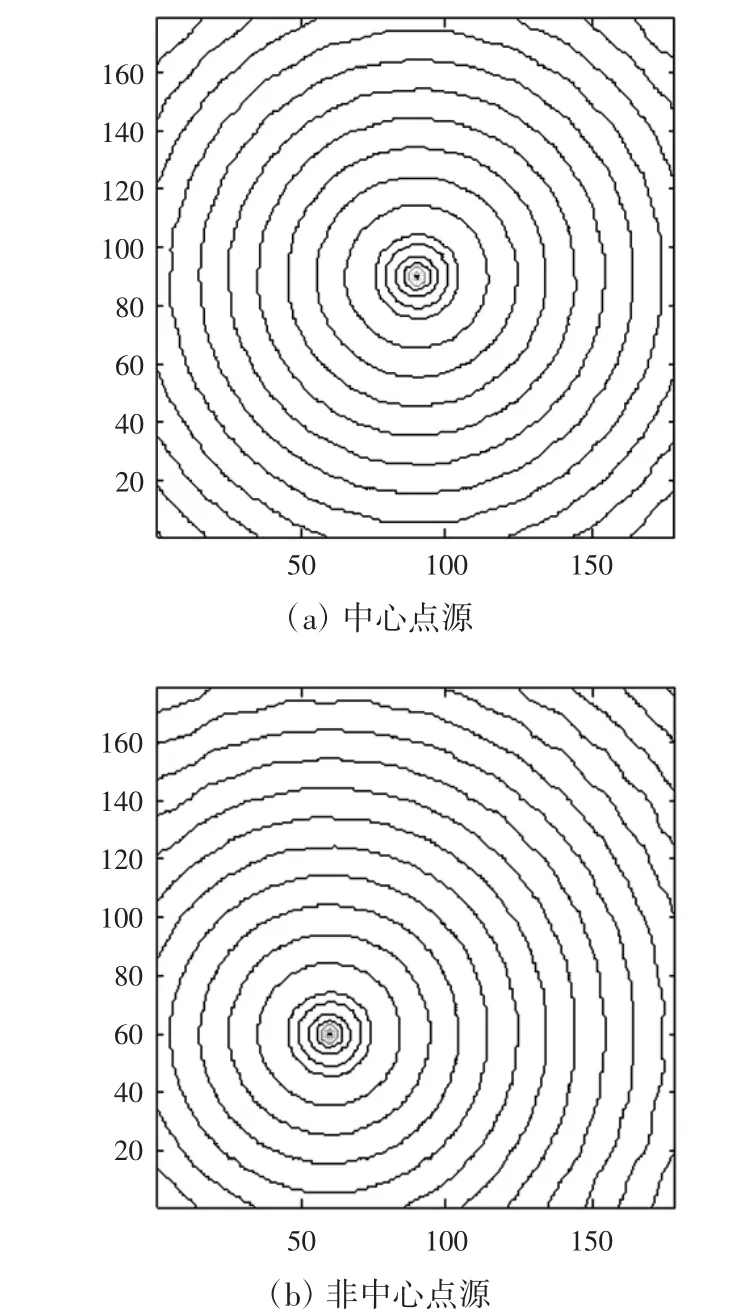
图4 正弦点源在媒质吸收薄层下吸收过程

4 结束语

本文利用媒质表面无反射条件，证明出阻抗匹配的条件，在精细结构中可以满足入射角与折射角相等，利用ADI-FDTD算法，对这种边界进行设计和相应的数值计算。从ADI-FDTD仿真中，能发现正弦波源无反射，这说明这种媒质吸收薄层设计是有效的。

［1］ YEE K S.Numerical solution of initial boundary value problem involving Maxwell′s equations in isotropic media[J]. IEEE Trans on AP，1966，14（3）：585-589.

［2］ NAMIKI T.A new FDTD algorithm based on alternatingdirection implicit method[J].IEEE Trans on MTT，1999，47（10）：2003-2007.

［3］ ZHENG F，CHEN Z，ZHANG J.A finite-differ ent timedomain method without the Courant stability condition[J]. IEEE Microwave Guided Wave Lett，1999，9（11）：441-443.

［4］ NAMIKI T，ITO K.Numerical simulation using ADI-FDTD method to estimate shielding effectiveness of thin conductive enclosures[J].IEEE Trans on MTT，2001，49（6）：1060-1066.

［5］ 付强，刘长军，严丽萍.ADI-FDTD算法的发展与改进[J].洛阳工业高等专科学校学报，2004，14（3）：1-3.

［6］ ZHANG Y，ZHENG H.An Isotropic PML for the FDTD Solver [C]//iWEM2012.Chengdu：iWEM，2012：2005.

［7］ 张玉贤，郑宏兴.时域有限差分法中的数值色散及误差分析［EB/OL］.［2014-03-02］.http：//www.paper.edu.cn/rele asepaper/content/201301-1223，2013.

［8］ 丁世敬，葛德彪，黄刘宏.电磁吸波材料中的阻抗匹配条件[J].电波科学学报，2009，24（6）：1104-1108.

［9］ 王仁乾，马黎黎.吸声材料物理参数优化的研究[J].声学技术，2004，23（2）：74-78.

［10］肖猛.复合吸波材料的阻抗匹配对电波暗室性能的影响[C]//盛志森.2010年第15届可靠性年会论文集.北京：电子工业出版社，2010：352-356.

Design of medium absorbing thin layer for alternate-direction implicit finitedifference time-domain method

ZHANG Yu-xian，ZHENG Hong-xing，JI Lei-lei
（Institute of Antenna and Microwave Techniques，Tianjin University of Technology and Education，Tianjin 300222，China）

In order to solve the boundary problem for alternating-direction implicit finite-difference time-domain method（ADI-FDTD），we design a thin medium layer on the truncation boundary.The iteration form of ADI-FDTD is given.It is proved that non-reflection condition can be realized in this medium when it satisfies the impedance-matched condition.Numerical results show that electromagnetic waves can be absorbed evidently in one-and two-dimensional cases.Almost nonreflection can be found.

ADI-FDTD；thin media；without reflection

TM154

A

2095－0926（2014）03－0012－04

2014-04-22

国家自然科学基金资助项目（61371043）；天津市应用基础及前沿技术研究计划（12JCYBJC10500）.

张玉贤（1989—），男，硕士研究生；郑宏兴（1962—），男，教授，博士，硕士生导师，研究方向为天线、微波电路和计算电磁学,