映射观下的组合问题
2014-02-28陈明
陈明
(遵义师范学院数学与计算科学学院,贵州遵义563002)
映射观下的组合问题
陈明
(遵义师范学院数学与计算科学学院,贵州遵义563002)
排列组合是中学数学内容中学生普遍感到困难的部分,作者用现代数学语言给出其中组合的解释和说明.
组合;映射;等价关系;陪集;商集;分类
排列组合在中学数学内容中,是学生普遍感到困难的部分.究其原因,有以下三个方面:首先,内容本身是教学难点;其次,在其定义及表述上难以理解;再次,解题思路及方法难以掌握.作者用现代数学的集合、计数、分类、陪集、商集与映射的观点及方法,对组合问题作了一些分析、归纳,试图对组合概念作较高层次的解释、说明,希望能对中学数学该部分内容的教学有所帮助或提高.
文中所讨论的集合均为有限集.为方便,记#A表示集合A的元素个数,Nn={1,2,…n}表示从1开始的n个自然数的集合,I(Nm,A)表示映集Nm到集A所有单射组成的集合.关于集合的映射计数法,可作如下定义
定义 若#A=n,当且仅当存在着一个双射f:A→Nn.
普通高中数学教材中对组合概念的叙述:
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
如上叙述之关键,在于取出的m个元素不存在顺序上的问题,并成一组即可.对此,我们设f∈(Nm, A)(其中#A=n),且f(Nm)=B,现如保持B而只改变其元间的顺序,显然,存在这样的g∈(Nm,A),且也有g(Nm)=B.这样,我们给出如下的组合
定义I(Nm,A)中(#A=n)所有的以B为象的单射给出一个“从n事物中一次取m事物的组合”.
另外,若定义I(Nm,A)上的一个关系R,对于f,g∈I(Nm,A),(m≤#A=n),当且仅当f(Nm)=g(Nm)时,称f与g有关系,表为f R g.显然,关系R满足自反性、对称性与传递性,故关系R是集合I∈(Nm,A)中元间的一个等价关系.由近世代数知识(张禾瑞《近世代数基础》28页定理2)知此等价关系R决定了集合I(Nm,A)的一个分类,每一个类叫做I(Nm,A)的一个陪集,所有陪集作成的集叫做I(Nm,A)的商集,记为I(Nm,A)/R.而每个陪集的意义为“从A中取m个元的组合”.因而,商集I(Nm,A)/R中的每一元也就等价于“n个事物中取个m元的一个组合”.从而计算组合数就只需计算陪集的个数:#(I(Nm,A)/R).
证明参见文献[1]中定理1.
推论 在定理1中,当n=m时,#(I(Nm,Nm)=
为了计算组合数,我们首先证明商集I(Nm,A)/R中所有陪集的元素个数均相等.
设f是I(Nm,A)/R中的任一元,因f是I(Nm,A)中的一个单射,这里设f(Nm)=B,显然,#B=m,且所有以B为象的单射个数,就等于B中m元的乱排数.故由定理1的推论知所有以B为象的单射个数为m!.这样,我们就推得f所在的陪集fR的元的个数为#f R=m!.又因f是任意的,所以商集I(Nm,A)/R中所有陪集元的个数均相等且为m!.
另外,由分类的定义可知I(Nm,A)由所有两两不交的陪集之并集所构成,由前面知陪集的个数用表示.从而有

由定理1,有

这样,我们得到了
定理2从n事物中取m事物的组合数为:
同样,这与中学课本上的组合数公式也是完全一致的.
以上采用导入方式给出定理.反之,如给出定理让其证明,那我们又可有如下的证法.
分析由定理2

因此,只需证明商集I(Nm,A)/R中,每一个陪集的元素个数都是m!即可.
证明当m=0时,因故关于模R仅有的陪集是自身.于是

定理2成立.
若m>0,由分析知,只需证每个陪集中单射的个数为m!即可.
为了证得#fR=m!,因#PermNm=m(!注:PermNm为Nm的全排列),故只需证#fR≈PermNm即可.为此,设法构造一个从fR到PermNm的双射.
∵PermNm是Nm→Nm
为了达到这一目的,我们固定一个元h∈fR,若g是可逆的,则有

由图1的线图可以看出:
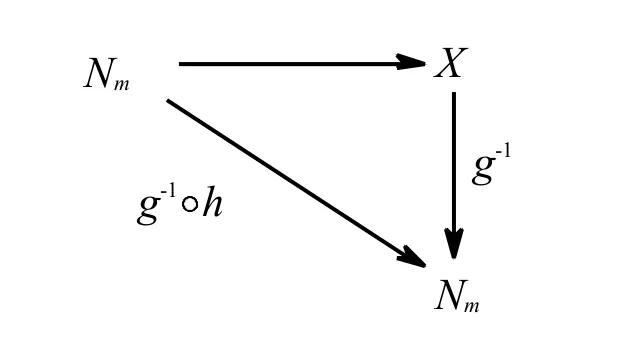
图1

(1)∵g∈I(Nm,A),∴g∶Nm→X是一对一的;
(2)又∵Im(g)=X∴g是在上的.
由(1)、(2)可推出:g∶Nm→X是一双射.
故g可逆,即g-1是存在的.从而上面定义的也就确实有效了.

图2
故由定理1之推论,有

如前所述,这就证明了定理2.
至此,我们利用集合、映射、陪集、计数的观点对组合进行了解释和说明.
关于中学数学教材对这一问题所采用的处理方式,主要是出于以下两方面的原因,一是学生的年龄特点;二是学生的知识结构.本文用现代数学的语言加以阐述,其目的是想说明现代数学与中学数学在这一部分内容上的内在联系.
[1]陈明.映射观下的排列问题[J].遵义师范学院学报,2012,14 (6):81-82.
[2]张奠宙,邹一心.现代数学与中学数学[M].上海:上海教育出版社,1990.
[3]陈明.排列组合之乘法原理探索[J].黔南民族师范学院学报, 2007,(6):37-38.
[4]H B格里菲思,P U希尔顿.经典数学综合教材[M].陈应枢,陈信传译.贵阳:贵州人民出版社,1986.
(责任编辑:朱 彬)
On the Combinatorial Problem from the perspective of Mapping View
CHEN Ming
(College of Mathematics and computing science,Zunyi Normal College,Zunyi 563002,China)
Permutation and combination are what high school students feel very hard in the maths contents of high school,and the author of this paper expounds the combination by modern mathematical expressions.
combination;mapping;equivalent relation;coset;quotient set;classification
O157
A
1009-3583(2014)-0104-03
2014-05-13
陈 明,男,贵州遵义人,遵义师范学院数学与计算科学学院副教授。
