两级高压涡轮三维时序效应研究
2014-02-28李昂薛伟鹏葛宁
李昂,薛伟鹏,葛宁
(1.南京航空航天大学能源与动力学院,江苏南京210016;2.中国燃气涡轮研究院,四川成都610500)
两级高压涡轮三维时序效应研究
李昂1,薛伟鹏2,葛宁1
(1.南京航空航天大学能源与动力学院,江苏南京210016;2.中国燃气涡轮研究院,四川成都610500)
为研究三维时序效应对多级涡轮效率的影响,采用课题组自主研发的三维CFD计算软件NUAA-Tur⁃bo,对GE公司高效节能发动机两级高压涡轮进行了非定常数值模拟。其中,边界条件的设置采用了相位延迟方法。计算结果表明,涡轮性能参数计算结果与实验数据基本吻合。先后验证了二维时序效应、三维时序效应对涡轮流场的影响,并利用非定常计算结果进行了分析。证实应用三维时序效应,可改变第一级转子叶片尾迹在第二级转子叶片前缘的相对位置,以及第二级转子叶片不同叶高处吸力面尾缘的附面层流动,最终能够提高涡轮效率。
高压涡轮;非定常计算;相位延迟法;弯曲叶片;三维时序效应
1 引言
在能源问题日趋严峻的今天,低耗油率成为民用航空发动机设计中最重要的技术指标之一。作为核心机三大部件之一的高压涡轮,其效率对航空发动机耗油率具有重大影响。
上世纪80年代初,美国NASA提出了高效节能发动机(E3)计划,目的是为下一代民用航空发动机研制提供技术储备。E3计划的成果被应用到后续许多大涵道比民用航空发动机中,GE90发动机更是直接应用了E3发动机的核心机技术。GE公司的E3发动机(GE-E3)中,采用了两级高压涡轮,其效率高达92.5%。因此,研究GE-E3两级高压涡轮内部流动特点,对我国先进高压涡轮设计具有重要指导意义[1]。
叶轮机内部转、静叶片的相对运动使得流动具有很强的非定常性,由此会产生时序效应。时序效应是指,叶轮机内同名叶栅(动叶与动叶或静叶与静叶)之间周向相对位置的改变,会引起叶轮机气动性能改变的现象。上世纪70年代,Walker最早发现时序效应能产生声学收益,可以降低叶轮机内转静交涉产生的噪声。到80年代中后期,时序效应对叶轮机性能的影响开始受到广泛关注。到目前为止,国内外已有很多学者对时序效应进行了研究[2,3]。就1.5级涡轮而言,时序效应对效率的提升在0.1%~0.7%之间[4];平面叶栅中甚至能达到2%[5]。大部分研究表明:当前一排同名叶片尾迹恰好撞在下一排叶片前缘上时,效率最高;当前一排同名叶片尾迹通过下一排叶片通道中部时,效率最低[3]。
三维时序效应是一个新概念,在CFM公司的新型涡扇发动机LEAP-X的涡轮上,设计者应用了三维时序效应来提高涡轮效率,如图1所示。图中黑实线为后排叶片的前缘,虚线为前排同名叶片的尾迹中心线。通过叶片弯曲的积叠线调整,使得尾迹中心线变为蓝色实线,周向更加聚拢;再通过调整两排叶片的周向相对位置,将前排同名叶片尾迹中心线移动到绿色实线位置,与下游叶片的前缘线很好地吻合。这种综合考虑不同叶高处的时序效应,保证涡轮总体性能最佳的方法,即为三维时序效应。三维时序效应已在国外先进发动机上得到了实用,证实其可有效提高叶轮机效率。
本文以GE-E3两级高压涡轮为例,通过非定常数值模拟,研究三维时序效应对涡轮性能的影响,并利用非定常计算结果分析涡轮效率上升的原因。
2 计算方法
2.1 几何模型与网格
GE-E3两级高压涡轮,采用等中径设计,中等负荷叶型。四排叶片数分别为46、76、48、70,具体的子午流道和各排叶片叶型参数取自文献[6]。为叙述方便,各排叶片分别命名为S1、R1、S2、R2。
采用自编程序对该两级涡轮绘制网格,如图2所示。叶片表面采用O型网格,势流区采用H型网格。四个叶排通道网格数分别为14.4万、13.7万、13.7万和14.1万,总网格量为55.8万。
2.2 数值解法与边界条件
采用课题组自行开发的基于结构化网格的CFD软件NUAA-Turbo进行计算。计算采用的绕X轴等Ω转速旋转的曲线坐标系下绝对速度的三维可压缩非定常N-S方程参见文献[7]。采用有限体积法数值求解,其中无粘对流通量的计算采用Roe格式,并运用具有二阶/三阶空间精度的Van Leer的MUSCL插值方法,粘性扩散通量则采用二阶中心差分格式计算。时间推进方面,采用牛顿迭代法隐式求解关于守恒变量的非线性方程组,对流通量的线化应用Roe近似雅可比矩阵,并采用多步对称高斯塞德尔(SGS)迭代求出牛顿线化后方程组的渐近解。湍流模型采用S-A模型。
定常隐式计算采用具有一阶时间精度的后差格式,非定常隐式计算则采用Jameson提出的具有二阶时间精度的双时间步法[8],且都采用当地时间步长方法加速解的收敛。定常计算时,转静交接面采用Denton提出的混合平面法;非定常计算,采用相位延迟方法给定周期边界条件和转静交接面边界条件。
根据文献[6]附录G中第11个状态点的实验数据,确定进口总压345 951.3 Pa,总温711.5 K,出口背压61 941.0 Pa,转速8 439.21 rad/min,轴向进气。
3 原始涡轮计算结果与分析
定常与非定常计算下得到的涡轮性能参数与实验值的对比见表1。其中,非定常结果为非定常计算收敛后一个周期内时均流场下所得结果。可见,定常计算的效率比实验值低1.14%,但压比、流量、功率与实验值基本吻合,能正确反映流场信息。非定常计算的效率较定常结果低1.08%,其他性能参数与定常结果和实验值基本一致。
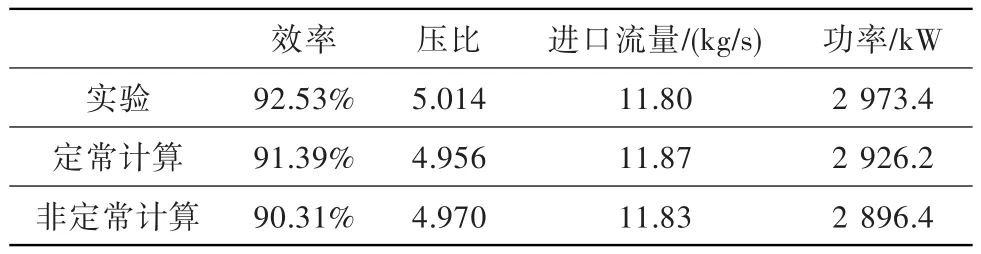
表1 定常与非定常计算涡轮性能参数与实验值的对比Table 1 Comparison of turbine performance parameter of steady and unsteady simulation
图3展示了非定常计算结果中一个周期四等分时刻下涡轮流场的熵分布。从图中可以看出,尾迹在叶片通道内的弯曲、拉伸、再定向等现象,与经典的尾迹输运理论[9]相符。因此,本文的非定常计算结果符合真实流场,在交接面处流动参数连续,证实了本文非定常计算方法的正确性。
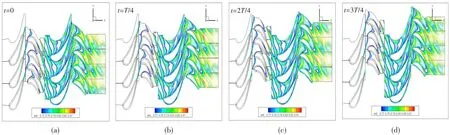
图3 一个周期四等分时刻下涡轮流场的熵分布Fig.3 Entropy distribution of turbine in different quarters
4 二维时序效应结果与分析
采用上述非定常计算方法,改变GE-E3两级高压涡轮中第二级转子的周向相对位置,研究转子二维时序效应。两个转子叶片叶根处前缘周向角度之差为0.232°,考虑转子时序效应时,改变R2叶片周向位置,初始位置为P1,每次逆时针旋转八分之一倍R2通道角,为0.625°,分别得到P2~P8时序位置,见图4中黑色圆点。
在上述8个不同转子时序位置下进行非定常计算,得到非定常收敛解,并求得时均流场下的效率,见图5。可见,P1时序位置涡轮效率最低,为90.31%;P5时序位置涡轮效率最高,为90.70%。为叙述方便,后文将P1、P5时序位置,分别命名为“最叙述方便,后文将P1、P5时序位置,分别命名为“最差时序位置”和“最佳时序位置”。
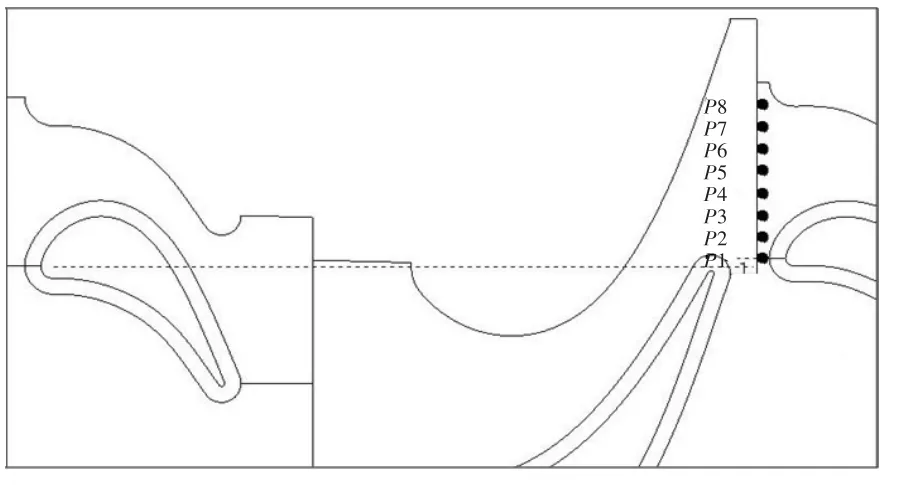
图4 涡轮转子叶片时序位置示意图Fig.4 Different clocking positions of rotor blade
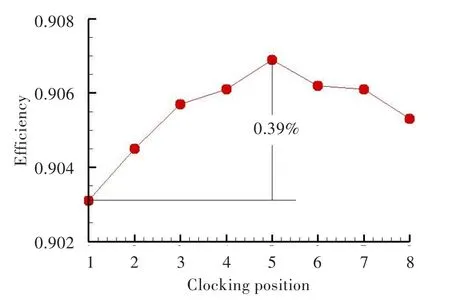
图5 不同转子时序位置下的涡轮效率Fig.5 Efficiency of turbine in different clocking positions
下面分析P1和P5时序位置效率差距的原因。图6为最差时序位置t=0时刻,R2通道内叶中截面和进口截面上的熵分布云图。其中图6(a)中通过箭头指出了S2叶片的尾迹(R2尾缘之前的红色区域),图6(b)中通过箭头指出了R1叶片的尾迹(R2尾缘之前的绿色区域)。时序效应中研究的是同名叶片尾迹相对位置带来的影响,本文计算中指的是前排R1叶片尾迹在后排R2通道处的周向位置。由于R1和R2叶片之间无相对运动,因此R1叶片尾迹总是出现在R2通道进口的相同周向位置。从图6(b)中可以看出,在R2通道进口截面上,R1尾迹1和R1尾迹4出现在R2通道中间。
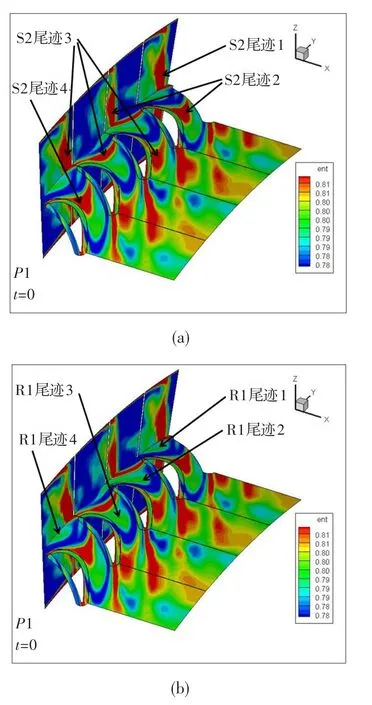
图6 P1时序位置t=0时刻R2通道的熵分布Fig.6 Entropy distribution of R2 in P1 clocking position and at time oft=0
图7为最差时序位置一个周期不同时刻下R2通道的熵分布图。由于R1叶片尾迹被R2叶片前缘切割,R1叶片尾迹在R2通道进口截面上呈现出空间间断性。可见,最差时序位置下,R1叶片尾迹输运到R2叶片前缘附近时,其周向位置总是出现在R2通道的中间,此时效率最低。这与时序效应的经典结论—当前一排同名叶片尾迹通过下一排叶片流道中部时效率最低一致。
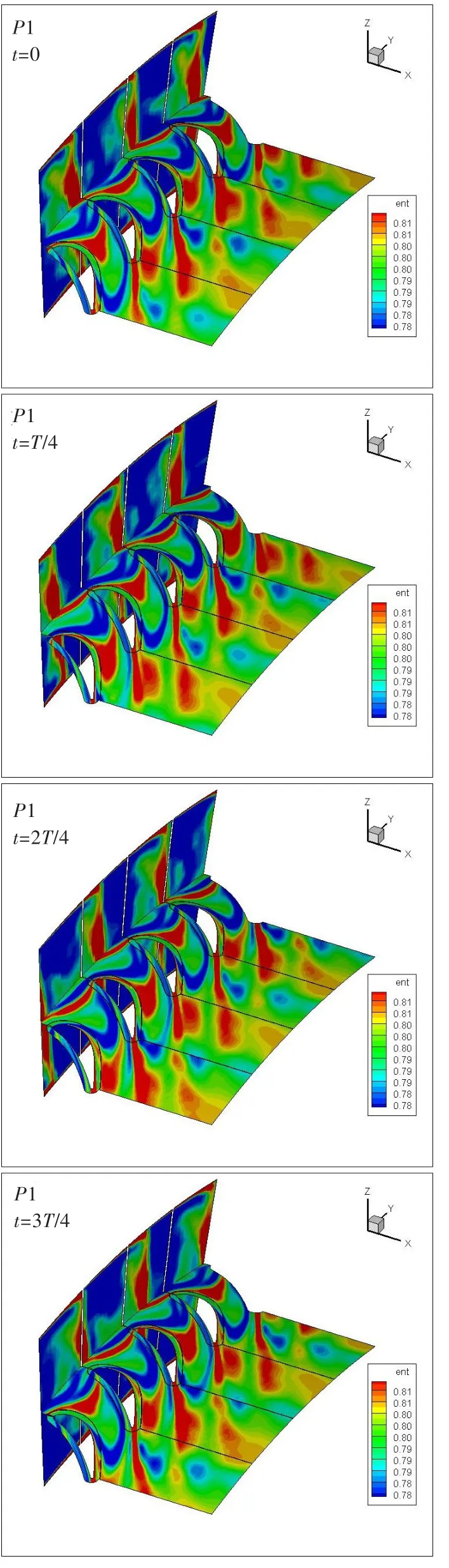
图7 P1时序位置不同时刻下R2通道的熵分布Fig.7 Entropy distribution of R2 in P1 clocking position and in different quarters
采用相同方法分析最佳时序位置下,R1叶片尾迹运动到R2叶片前缘时的周向位置,见图8。对比图7和图8可以看出,图8中绿色区域代表的R1叶片尾迹范围明显比图7中的小,这是由于最佳时序位置下R1叶片尾迹打到了R2叶片前缘,而不是从R2通道中间流过。因此最佳时序位置下,R1叶片尾迹输运到R2叶片前缘附近时,其周向位置总是可以打到R2叶片前缘,此时效率最高。这与时序效应的经典结论—当前一排同名叶片尾迹恰好撞在下一排叶片前缘上时效率最高一致。
综上所述,对于GE-E3两级高压涡轮,通过调整转子时序位置,改变了上游转子R1叶片尾迹在R2叶片通道内的周向相对位置。当时序位置保证R1叶片尾迹可以尽可能多地撞在R2叶片前缘上时,即本次计算中的最佳时序位置,可得到最高的涡轮效率。
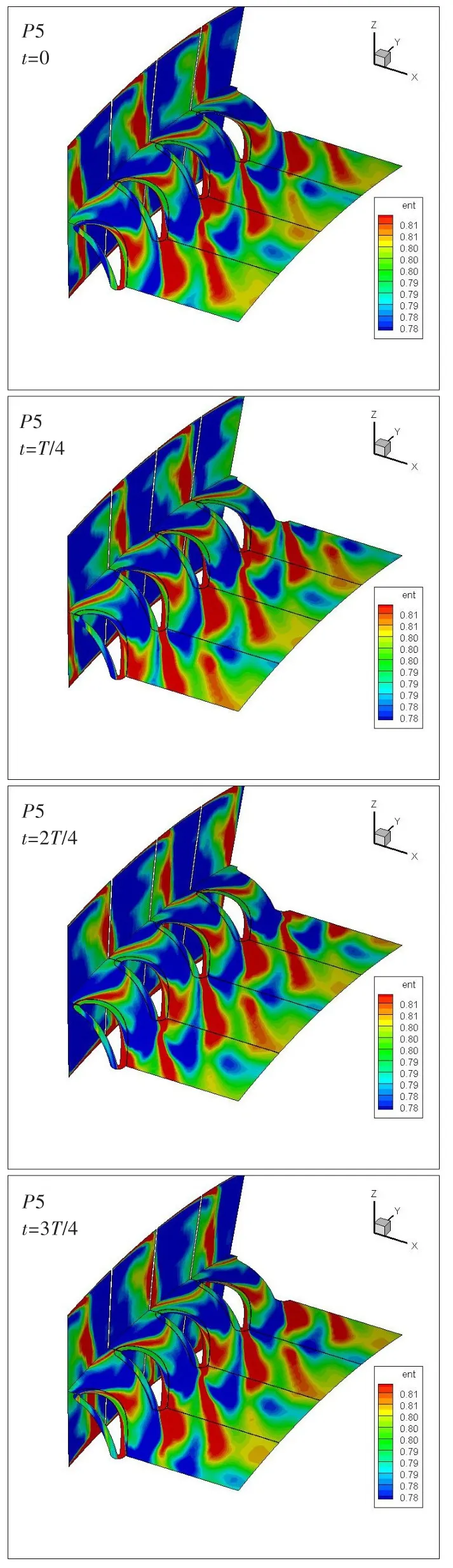
图8 P5时序位置不同时刻下R2通道的熵分布Fig.8 Entropy distribution of R2 in P5 clocking position and in different quarters
5 三维时序效应结果与分析
参考LEAP-X发动机,在GE-E3两级高压涡轮中,将叶片弯曲和周向时序位置调整相结合,研究三维时序效应。对于非定常计算结果,采用损失功的方法来分析各排叶片中的损失,结果显示R2叶片通道的损失最大,因此针对R2叶片进行弯曲设计。
本文计算状态下,R2叶片吸力面尾缘中间叶高无流动分离,因此采用叶片正弯。冯国泰[10]指出,动叶采用弯叶片时最佳倾角在一般条件下比较小,因此本文设计中叶根和叶尖的弯角都为10°。原始R2直叶片和正弯10°后的R2叶片如图9所示。
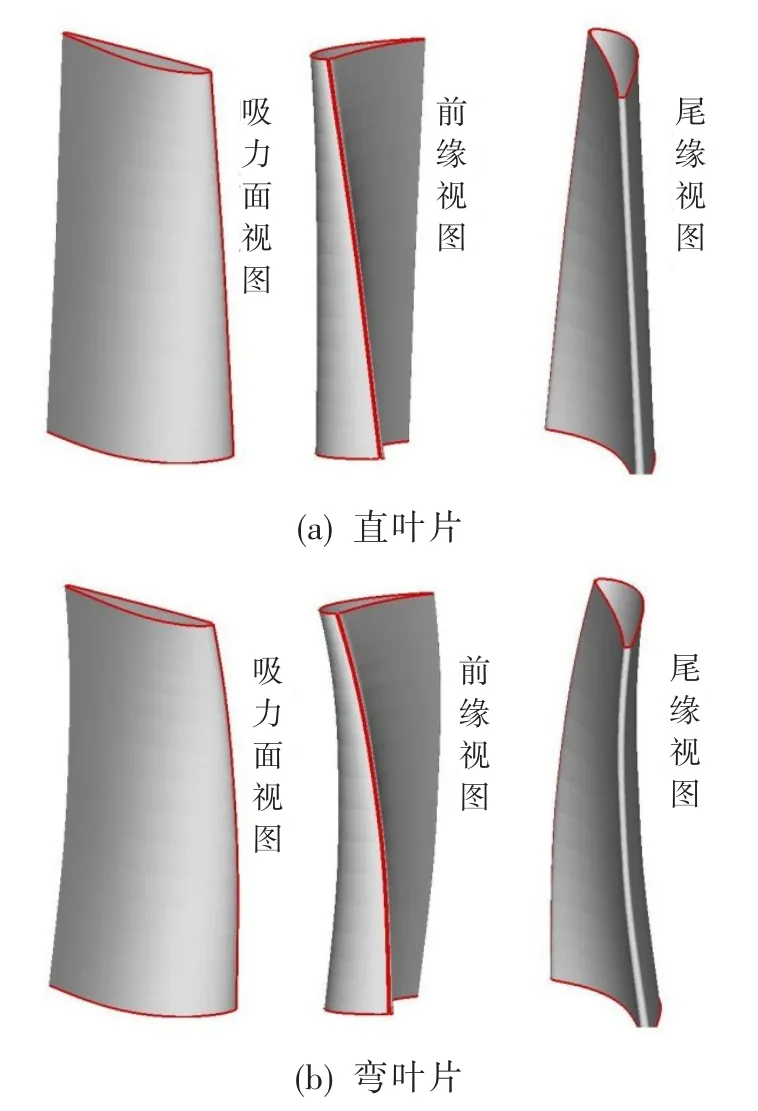
图9 R2叶片Fig.9 R2 blade
针对GE-E3两级高压涡轮的三维时序效应研究中,采用最佳时序位置与R2叶片正弯10°相结合,考察这一情况下涡轮的性能,并与原始涡轮、最佳时序位置下涡轮的性能进行对比,结果见表2。可见,利用三维时序效应,在最佳时序位置下进行叶片弯曲的积叠线调整,涡轮压比、流量基本不变的同时效率进一步上升到90.89%,相比最佳时序位置下直叶片效率提高了0.19%,相比原始涡轮效率提高了0.58%。
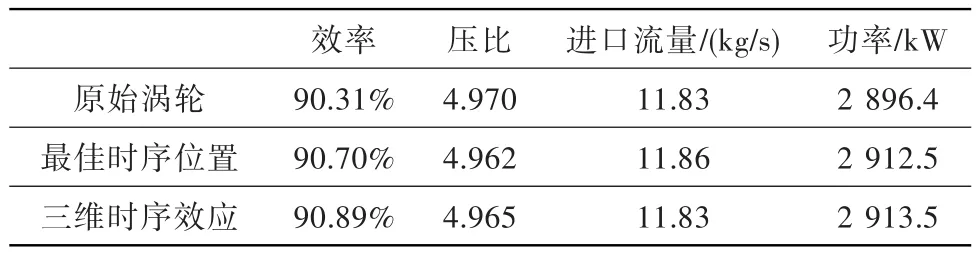
表2 涡轮性能参数对比Table 2 Comparison of turbine performance parameter
下面分析R2叶片正弯后效率进一步上升的原因。图10为最佳时序位置下直叶片与弯叶片算例中,涡轮第二级的沿叶高反力度对比。可见,在最佳时序位置下,将R2叶片正弯10°,涡轮第二级不同叶高的反力度几乎不变,即本文条件下叶片变弯后并未改变涡轮第二级中负荷的分配状况。
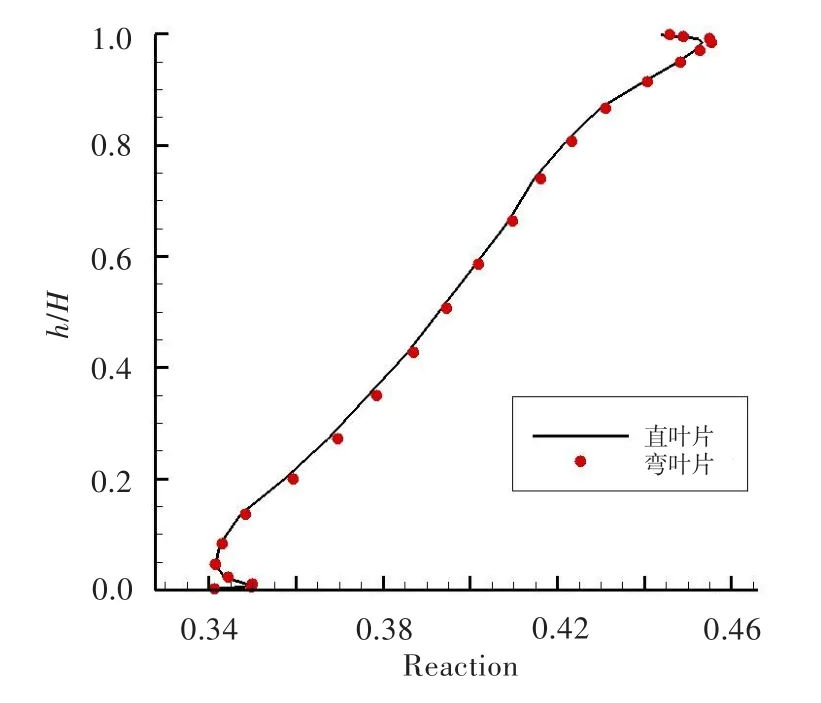
图10 P5时序位置下涡轮第二级沿叶高反力度Fig.10 Reaction of 2nd stage in P5 clocking position
图11为最佳时序位置下R2叶片通道叶中截面的熵分布云图。可见,两图中R1尾迹与S2尾迹的大小和位置基本相同,但弯叶片图中R2叶片尾迹范围相对较窄,同位置下的熵值也较小。也就是说,在最佳时序位置下经叶片正弯后,会使中间叶高附近R2叶片尾迹强度降低,从而降低损失。
图12为最佳时序位置下,R2叶片叶中截面尾缘附近的马赫数图。可见,最佳时序位置下R2叶片正弯后,中间叶高处吸力面尾缘附面层变薄。其原因为,叶片正弯改变了吸力面尾缘中间叶高处附面层的流动情况,另外也改变了此处附面层与S2叶片尾迹的耦合作用,使得此处附面层变薄,最终产生R2叶片尾迹强度降低的结果。
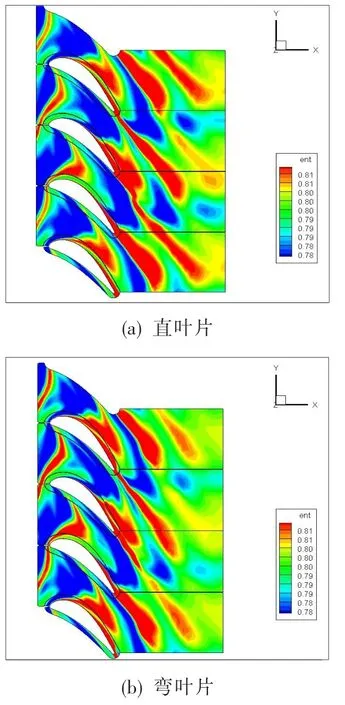
图11 R2叶片通道叶中截面的熵分布Fig.11 Entropy distribution of R2 blade passage of mid-span
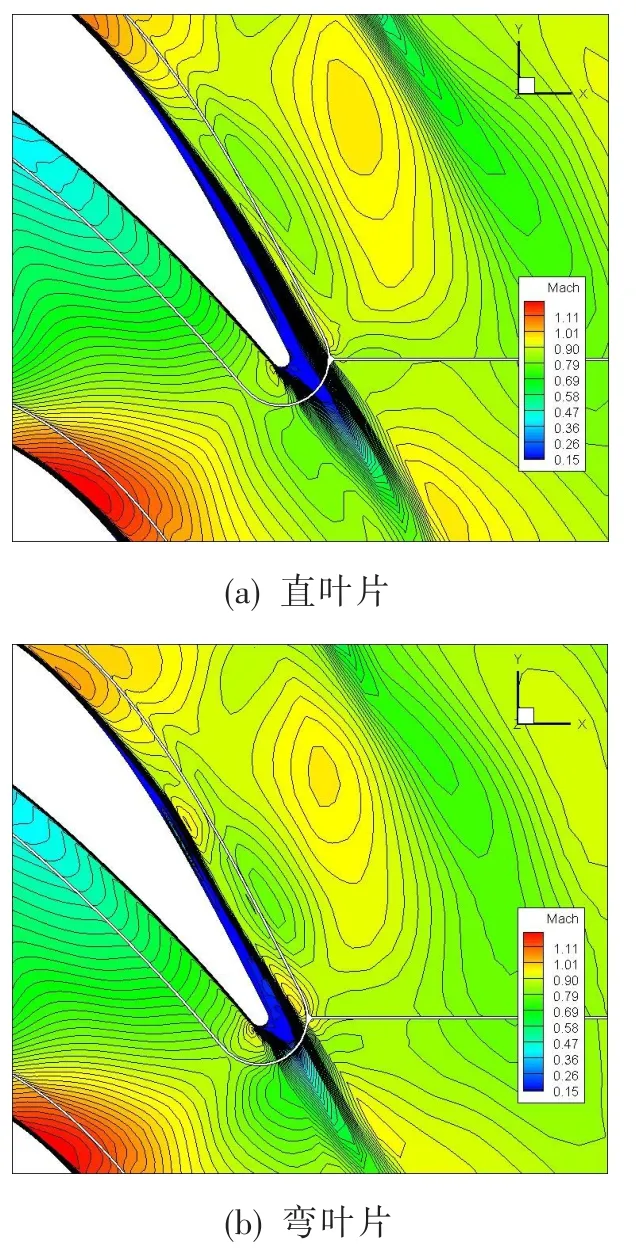
图12 R2叶片叶中截面尾缘的马赫数分布Fig.12 Mach distribution of R2 blade tail of mid-span
综上所述,通过结合了时序位置调整与积叠线调整的三维时序效应,改进了GE-E3两级高压涡轮,使其效率提高到了90.89%。相比最佳时序位置下算例效率提高了0.19%,相比原始涡轮效率提高了0.58%。利用非定常计算结果进行分析,涡轮效率提高的原因是:叶片周向时序位置移动后,使得R1叶片尾迹打到R2叶片前缘,令相对低速的尾迹区域与叶片表面附面层混合,降低了通道中的损失;R2叶片积叠线调整后,可改变不同叶高处吸力面尾缘附面层的流动情况,使中间叶高处吸力面尾缘变薄,从而使得尾迹范围变窄、强度减弱,使得R2叶片尾迹带来的损失降低,最终提高了涡轮效率。
6 结论
本文运用课题组自行开发的三维CFD软件NU⁃AA-Turbo进行了两级高压涡轮的非定常数值模拟,研究了三维时序效应对涡轮性能的影响,并利用非定常计算结果进行了分析,可得到以下两点结论:
(1)对于本文计算采用的两级高压涡轮,利用二维时序调整转子时序位置,可改变R1叶片尾迹与R2叶片前缘的相对位置,最佳时序位置下涡轮效率能提高0.39%。
(2)利用三维时序效应,将转子时序位置调整与叶片弯曲相结合,进一步改变叶片吸力面附面层分布情况,可使涡轮效率提高0.58%。在多级叶轮机中,合理利用三维时序效应,能有效提高涡轮效率。
[1]曾军,王彬,卿雄杰.某双级高压涡轮全三维计算[J].航空动力学报,2012,27(11):2553—2561.
[2]Reinmöller U,Stephan B,Schmidt S,et al.Clocking Ef⁃fects in a 1.5 Stage Axial Turbine-Steady and Unsteady Experimental Investigations Supported by Numerical Simu⁃lations[J].ASME 2001-GT-0304,2001.
[3]侯安平,周盛.轴流式叶轮机时序效应的机理探讨[J].航空动力学报,2003,18(1):70—75.
[4]李红丽,乔渭阳.静叶时序对高压涡轮性能影响的数值研究[J].科学技术与工程,2012,12(17):4221—4225.
[5]Dorney D J,Sharma O P.A Study of Turbine Performance Increases through Airfoil Clocking[R].AIAA 1996-2816,1996.
[6]Timko L P.Energy Efficient Engine High Pressure Tur⁃bineComponentTestPerformanceReport[R].NASA CR-168289,1990.
[7]Chen J P.Unsteady Three-Dimensional Thin-Layer Navi⁃er-Stokes Solutions for Turbomachinery in Transonic Flow [D].Mississippi:Mississippi State University,1991.
[8]Jameson A.Time Dependent Calculations Using Multigrid with Application to Unsteady Flows Past Airfoils and Wings[R].AIAA 91-1596,1991.
[9]Stieger R D,Hodson H P.The Unsteady Development of a Turbulent Wake through a Downstream Low-Pressure Tur⁃bine Blade Passage[J].ASME GT2004-53061,2004.
[10]冯国泰,顾中华,王松涛.具有弯扭掠叶片流场结构分析能力的燃气涡轮三维设计体系[J].航空发动机,2002,28(4):5—9.
3D-Clocking Effect on Two-Stage High Pressure Turbine
LI Ang1,XUE Wei-peng2,GE Ning1
(1.College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.China Gas Turbine Establishment,Chengdu 610500,China)
In order to study the influence of 3D-Clocking effect in multistage turbine,the 3D CFD software NUAA-Turbo was used to simulate the GE-E3two-stage high pressure turbine,and the phase-lag method was used in setting boundary conditions.The calculation result of turbine performance parameter was con⁃sistent with experiment data approximately.Farther more,the influence of 2D-Clocking and 3D-Clocking effect on turbine performance was validated,and the reason was discussed by unsteady results.Finally,the turbine efficiency increase caused by 3D-Clocking effect was confirmed,by changing relative position of upstream rotor wake in downstream rotor and changing distribution of boundary layer in suction surface of downstream rotor R2.
high pressure turbine;unsteady numerical simulation;phaselag method;bowed blade;3D-Clocking effect
V231.3
:A
:1672-2620(2014)04-0012-06
2013-10-08;
:2014-03-20
李昂(1989-),男,吉林省吉林市人,硕士研究生,主要从事叶轮机气动力学研究。
