涡轮盘低循环疲劳寿命预测方法与流程

魏芷峰，王延荣，袁善虎，石亮

(北京航空航天大学能源与动力学院，北京100191)

涡轮盘低循环疲劳寿命预测方法与流程

魏芷峰，王延荣，袁善虎，石亮

(北京航空航天大学能源与动力学院，北京100191)

发展了一种涡轮盘低循环疲劳寿命预测方法及流程，其重点在于材料疲劳参数的确定、考虑多重影响因素的疲劳寿命预测方法，及涡轮盘结构的寿命预测，并以GH901合金涡轮盘为例进行了分析。结果表明：所发展的寿命预测方法及流程，可保证材料疲劳参数，同时具有明确的物理意义和良好的数值准确性；采用考虑梯度影响的疲劳寿命预测方法，在较少试验和计算量的基础上，考虑平均应力、应力梯度和尺寸效应的影响，对GH901合金缺口试样和实际涡轮盘试验件的疲劳寿命预测均较为理想，在2倍分散带以内。

航空发动机；涡轮盘；低循环疲劳；疲劳参数；平均应力；应力梯度；寿命预测

1 引言

涡轮盘作为航空发动机关键热端结构件，其轮盘连接孔、冷却孔等几何不连续区域会产生明显的应力集中，在高温、高转速条件下，成为疲劳裂纹萌生乃至疲劳破坏的主要原因。因而，发展一种发动机涡轮盘低循环疲劳寿命预测方法及流程，对于发动机结构完整性和可靠性具有重要意义。

预测结构件疲劳寿命，首先需要确定结构件的材料疲劳参数，而材料疲劳参数以疲劳寿命预测方程为基础。众多的寿命预测方程[1-4]中，总应变寿命方程既可反映应变为主导的低循环疲劳特征，又可反映应力为主导的高循环疲劳特征，且应用最为广泛，因而材料手册[5]中通常给出该方程的相应参数值作为材料的疲劳参数。疲劳参数的确定有诸多方法，如简单近似法[6]、四点相关法[7]、通用斜率法[8]等，如何根据疲劳参数的物理意义，准确确定参数值对疲劳寿命预测的准确性十分重要。

在明确材料疲劳参数的基础上，还需考虑影响结构疲劳寿命的主要因素，如载荷特性、温度、应力集中、尺寸效应等。由于实际结构影响疲劳寿命的因素多且复杂，材料疲劳试验不可能全部囊括，因而根据这些因素对疲劳寿命的影响规律，发展了许多考虑实际影响因素的疲劳寿命预测方法。如载荷特性中考虑平均应力影响，Morrow[9]、Smith[10]和Walker[11]等都提出了各自的平均应力修正模型，并在疲劳寿命预测中得到广泛使用；Dowling[12]对目前广泛应用的考虑平均应力影响的四种模型进行了对比。而针对应力集中构件疲劳寿命的预测方法，主要有名义应力法[13]、局部应力应变法[14-15]和临界距离法[16-18]等。因而在众多考虑疲劳寿命影响因素的预测方法中，确定一种既能考虑诸多影响因素，又能尽量降低对大量试验的依赖且计算相对简单的寿命预测方法，对于工程应用十分重要。

本文在众多疲劳寿命研究的基础上，发展了一种发动机涡轮盘低循环疲劳寿命的预测流程，如图1所示，研究疲劳参数确定方法选用、考虑诸多影响因素的缺口疲劳寿命预测方法选用及其在结构件上的应用，并以GH901合金涡轮盘为例进行检验计算，以期为工程实际中涡轮盘低循环疲劳寿命预测提供一条可行的途径。

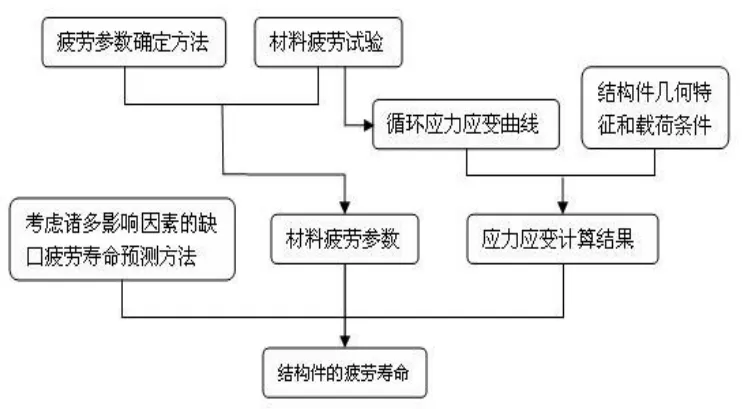
图1 结构件低循环疲劳寿命预测流程Fig.1 Low-cycle fatigue life prediction procedure for structural components

2 材料疲劳参数的确定

材料手册中通常给出总应变寿命方程参数作为低循环疲劳参数，其形式为：

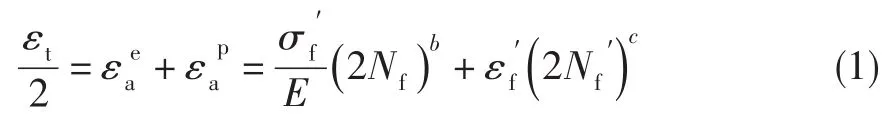
式中：εt为总应变范围，为弹性应变幅，为塑性应变幅，E为弹性模量，Nf为材料或构件的疲劳寿命，为疲劳强度系数，b为疲劳强度指数，为疲劳延性系数，c为疲劳延性指数。以上4个材料参数需根据试验结果获得，但由于总应变方程在双对数坐标系下不再是简单的线性关系，不易直接通过线性拟合得到。王延荣等[19]通过建立总应变方程中疲劳强度系数及疲劳延性系数，与单调拉伸时强度极限和断面收缩率之间的关系，发展了一种新的总应变方程参数的确定方法，关系式为：

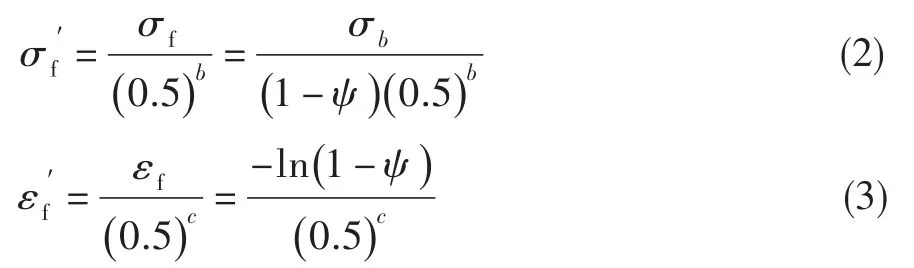
式中：σf为一次单调拉伸时的断裂真应力，εf为断裂真应变，σb为材料拉伸强度极限，ψ为断面收缩率。以上参数均可通过材料手册查得或材料试验获得。将式(2)、式(3)代入式(1)并结合疲劳试验数据，可拟合得到b和c，进一步可得到。该方法可保证总应变方程中参数具有明确的物理意义，同时采用拟合得到的参数对3种材料进行寿命预测的结果十分理想，因而涡轮盘低循环疲劳寿命预测流程中采用该方法确定材料的疲劳参数。王延荣等[19]给出了根据材料手册试验数据拟合得到的GH901合金低循环疲劳参数，及采用拟合得到的参数进行疲劳寿命预测的结果，见表1和图2。可见，该方法给出的参数值既符合参数的物理意义，又能在较大寿命范围内较好地预测材料的疲劳寿命。

表1 500℃下GH901合金的低循环疲劳参数Table 1 Fatigue parameters of GH901 alloy at 500℃

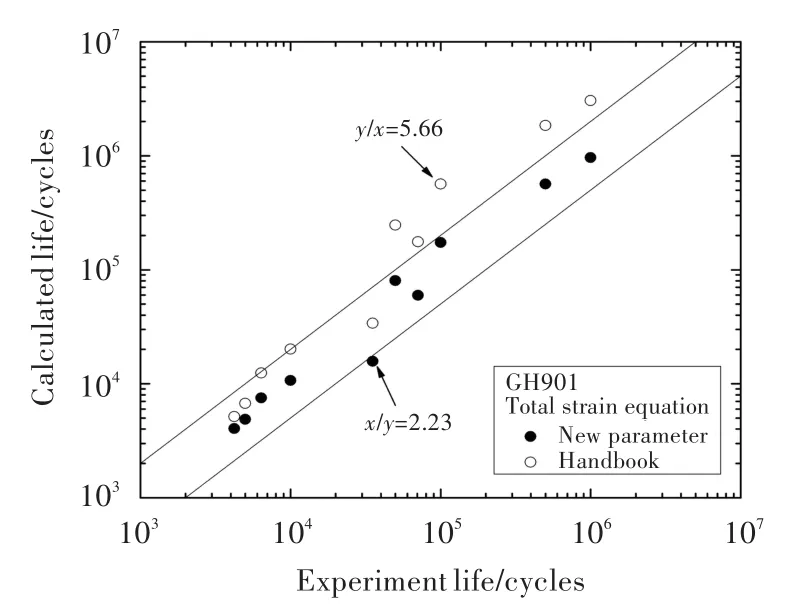
图2 GH901合金两种参数总应变寿命方程的预测结果Fig.2 Life prediction by total strain equation with two kinds of parameters for GH901 alloy

3 考虑多种影响因素的疲劳寿命预测方法

疲劳分析中经常遇到载荷(平均应力、载荷波形)、应力集中、尺寸效应(均匀应力场、非均匀应力场)等影响因素，在寿命预测方程中如何体现这些影响因素，对寿命方程预测的准确性十分重要。文献[20]在研究缺口应力应变分布的基础上，给出了一种综合考虑平均应力、应力梯度和尺寸效应的疲劳寿命预测方法，其寿命预测方程为：

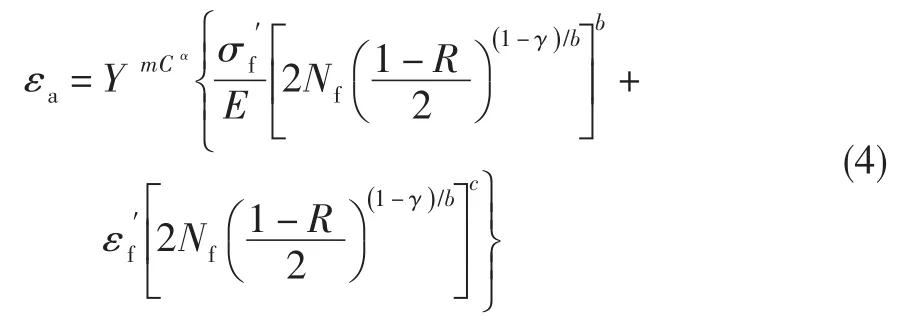
式中：Y为应力梯度影响因子；C为尺寸影响因子，刻画尺度效应；α为尺寸效应影响指数；R为应力比；m为应力梯度影响指数，且与Nf存在如下关系

式中：A、B为常数。本节采用该方法开展GH901合金缺口试样的疲劳寿命预测，以检验其预测精度。

3.1 应力比的影响

材料手册[5]给出的GH901合金在500℃下的疲劳试验数据见表2，基于表2中疲劳寿命结果拟合得到的Walker平均应力修正参数见表3。

表2 GH901合金试样500℃下的疲劳性能Table 2 Fatigue properties of GH901 at 500℃

表3 Walker寿命方程中的参数Table 3 Parameters in Walker life equation

图3给出了GH901合金平均应力修正的寿命预测结果，图中Nw为Walker寿命方程得到的等效寿命，。可见，Walker平均应力修正方程，对不同应力比条件下试样的寿命预测均十分理想。

图3 Walker平均应力修正的寿命曲线Fig.3 Life curve modified by Walker’s mean stress

3.2 应力梯度的影响

对缺口圆棒试样进行轴对称线弹性有限元分析，缺口局部的应力分布见图4，试样缺口平分线上归一化应力分布见图5。图中，σmax为缺口根部最大应力，σ为缺口平分线上不同位置应力，x为距缺口根部的距离，r为缺口根部半径。求得Y=1/(2S0.5)=1.421 4。

图4 缺口圆棒试样局部应力分布Fig.4 Local stress distribution of notched round specimen

图5 GH901合金缺口试样缺口平分线上归一化应力分布Fig.5 Normalized stress distribution along symmetric path for notched specimens of GH901 alloy

采用Neuber法计算缺口试样(Kt=3)局部应力应变，结合对称加载条件(R=-1.0)下的疲劳试验数据，对m的参数A和B进行拟合，结果如图6所示。

图6 梯度影响指数与2Nf的关系Fig.6 Gradient effect exponentmversus2Nf

3.3 缺口试件疲劳寿命预测

利用Neuber法计算缺口试件在不同应力比条件下的局部应力应变，结合考虑应力梯度的寿命方程，对不同应力比条件下缺口试件进行寿命预测，结果见表4和图7。由图7可看出，考虑应力梯度的寿命预测方程，对应力比-1.0和0.1条件下的GH901合金缺口试样寿命预测结果十分理想，其分散带在2倍以内。

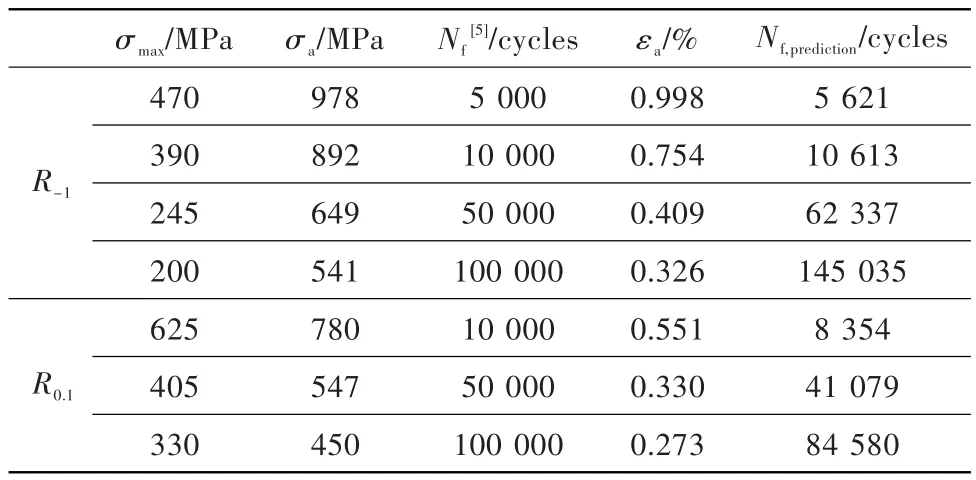
表4 缺口试件寿命预测结果Table 4 Life prediction of notched specimen

图7 缺口试件寿命预测结果Fig.7 Predicted life of notched specimen

4 涡轮盘疲劳寿命预测

结构件示例分析采用文献[21]给出的涡轮盘试验件，其材料为GH901合金，试验条件为：均温525℃，转速范围650～12 640 r/min。试验结果表明，轮盘销钉孔边为疲劳破坏区域，孔边裂纹萌生寿命为3 435次循环。

选用MSC.MARC有限元分析软件，建立涡轮盘扇区(1/16圆周)有限元模型，如图8所示。单元类型为八节点六面体实体单元，网格进行了加密以提高计算精度。

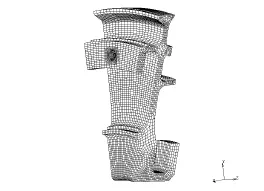
图8 轮盘扇区(1/16圆周)有限元模型Fig.8 FE model of the turbine disk sector

轮缘施加外载荷131.74 MPa，以模拟叶片离心力，转速为12 640 r/min，扇区两侧面施加循环对称约束，盘与轴连接处约束轴向和周向位移，整体模型均温525℃。轮盘的周向应力、应变分布分别如图9和图10所示。

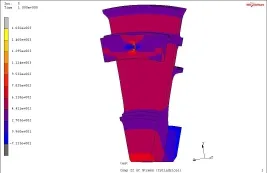
图9 轮盘周向应力分布Fig.9 Hoop stress distribution of the turbine disk

图10 轮盘周向应变分布Fig.10 Hoop strain distribution of the turbine disk

销钉孔边归一化周向应力沿对称平分线归一化距离的分布曲线如图11所示，进一步计算可得轮盘销钉孔边应力梯度影响因子Ydisk=1.356 5。m与Nf的关系式采用GH901合金缺口试样疲劳试验数据拟合得到，m=29.65(2Nf)-0.253。

图11 轮盘销钉孔边周向归一化应力-归一化距离分布Fig.11 Normalized hoop stress distribution along normalized symmetric path of the turbine disk pin-hole

涡轮盘及材料标准缺口试件的局部归一化应力-距离分布如图12所示，计算得C=0.113 8。由于GH901材料仅有Kt=3的试验数据，无法拟合得到α，因而轮盘模型中的α参考其他材料数据[20]给定为0.3。

图12 轮盘销钉孔边周向归一化应力-距离分布Fig.12 Normalized hoop stress distribution along symmetric path of the turbine disk pin-hole

基于以上参数计算结果及Neuber法计算的销钉孔局部弹塑性最大应力和局部应变，采用考虑应力梯度的疲劳寿命预测方法，对涡轮盘进行寿命预测，结果见表5。可见，考虑多种影响因素的轮盘寿命预测值较为理想，在2倍分散带以内。

表5 轮盘寿命预测结果Table 5 Life prediction of turbine disk

5 结论

通过对GH901合金材料疲劳参数确定、缺口试样寿命预测及GH901合金涡轮盘疲劳寿命预测，确立了一种结构件疲劳寿命预测方法及流程。

(1)材料疲劳参数作为结构件疲劳寿命预测的基础，对构件寿命预测的准确性起着至关重要的作用，采用所发展的寿命预测流程确定的材料疲劳参数，既可保证其有明确的物理意义，又可保证其数值的准确性。

(2)所发展的寿命预测流程采用的考虑应力梯度的寿命预测方法，在尽量降低疲劳试验和计算量的基础上，综合考虑了平均应力、应力梯度和尺寸效应的影响，对GH901缺口试样寿命预测在2倍分散带以内。

(3)所发展的寿命预测流程很好地建立了结构件与标准试样之间的关系，对GH901涡轮盘低循环疲劳寿命预测结果较为理想，在2倍分散带以内。

(4)本文基于已有研究发展的寿命预测流程，一方面可有效利用材料手册中现有数据，降低寿命预测对大量试验的依赖；另一方面又充分考虑了各种影响因素，提高了寿命预测精度，为工程实际结构件的疲劳寿命预测提供了一条切实可行的途径。

[1]Basquin O H.The Exponential Law of Endurance Tests[J]. American Society for Testing and Materials Proceedings，1910，10：625—630.

[2]Manson S S.Behavior of Materials under Conditions of Thermal Stress[R].NACA TN-2933，1953.

[3]Coffin L F Jr.A Study of the Effect of Cyclic Thermal Stresses on a Ductile Metal[M].New York：Knolls Atomic Power Laboratory，1953.

[4]Morrow J D.Cyclic Plastic Strain Energy and Fatigue of Metals[R].ASTM STP 378，1964.

[5]中国航空材料手册编辑委员会.中国航空材料手册[M].北京：中国标准出版社，1988.

[6]Draper J.Modern Metal Fatigue Analysis[M].Sheffield，UK：EMAS Publishing Company，1999.

[7]Manson S S.Fatigue:A Complex Subject-Some Simple Approximations[J].Experiment Mechanics，1965，5(7)：193—226.

[8]Socie D F，Mitchell M R，Caulfield E M.Fundamentals of Modern Fatigue Analysis[R].Illinois：University of Illi⁃nois，1977.

[9]Morrow J D.Fatigue Design Handbook Section 3.2[J].Soci⁃ety for Automotive Engineers(SAE)Advances in Engineer⁃ing，1968，4(1)：21—29.

[10]Smith K N，Watson P，Topper T H.A Stress-Strain Func⁃tion for the Fatigue of Metals[J].Journal of Materials，1970，5(4)：767—778.

[11]Walker K.The Effect of Stress Ratio during Crack Propa⁃gation and Fatigue for 2024-T3 and 7075-T6 Aluminum [R].ASTM STP 462，1970.

[12]Dowling N E.Mean Stress Effects in Stress-Life and Strain-Life Fatigue[C]//.Second SAE Brasil International Conference on Fatigue.San Paulo，2004.

[13]姚卫星.结构疲劳寿命分析[M].北京：国防工业出版社，2002.

[14]Topper T H，Wetzel R M，Morrow J.Neuber’s Rule Ap⁃plied to Fatigue of Notched Specimens[J].Journal of mate⁃rials，1969，4(1)：200—209.

[15]Dowling N E，Brose W R，Wilson W K.Notched Member Fatigue Life Prediction by the Local Strain Approach[J]. Advances in Engineering Fatigue under Complex Loading SAE，1977，6：55—84.

[16]Qylafku G，Azari Z，Gjonaj M，et al.On the Fatigue Fail⁃ure and Life Prediction for Notched Specimens[J].Materi⁃als Science，1998，34(5)：604—618.

[17]Luca S，David T.An Elasto-Plastic Reformulation of the Theory of Critical Distances to Estimate Lifetime of Notched Components Failing in the Low/Medium-Cycle Fatigue Regime[J].Journal of Engineering Materials and Technology，2010，132(2)：021002.1—021002.8.

[18]Luca S.The Theory of Critical Distances:A Review of Its Applications in Fatigue[J].Engineering Fracture Mechan⁃ics，2008，75(7)：1706—1724.

[19]王延荣，李宏新，袁善虎，等.确定总应变寿命方程参数的一种方法[J].航空动力学报，2014，29(4)：881—886.

[20]王延荣，李宏新，袁善虎，等.考虑应力梯度的缺口疲劳寿命预测方法[J].航空动力学报，2013，28(6)：1208—1214.

[21]杨俊，张贵斌，祁圣英，等.涡轮盘传动臂销钉孔低循环疲劳寿命分析[J].机械科学与技术，2011，30(9)：1490—1494.

Life Prediction Method and Procedure for Low-Cycle Fatigue of Turbine Disk

WEI Zhi-feng，WANG Yan-rong，YUAN Shan-hu，SHI Liang
(School of Energy and Power Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

A low-cycle fatigue life prediction procedure for turbine disk was developed.The study focused on the determination of material fatigue parameters,fatigue life prediction methods with multiple influential factors considered and life prediction of turbine disk.Furthermore,the life prediction procedure was used to predict the fatigue life of turbine disk made of GH901 alloy.The results show that the fatigue parameters ob⁃tained by the developed procedure have both definite physical significance and good numerical accuracy and the fatigue life prediction method adopted considers the effects of mean stress,stress gradient and di⁃mensional size on the basis of limited experiments and calculated amount.The life predictions give esti⁃mates falling within a scatter of two for notched specimens and turbine disk.

aero-engine；turbine disk；low-cycle fatigue；fatigue parameter；mean stress；stress gradient；life prediction

V231.9；V232.3

：A

：1672-2620(2014)05-0025-05

2013-09-02；

：2014-02-25

魏芷峰(1990-)，男，吉林德惠人，硕士研究生，主要从事高温结构强度与疲劳等方面的研究。