湍流燃烧模型在燃烧室数值模拟中的对比分析
2014-02-28刘重阳戴斌
刘重阳,戴斌
(中国燃气涡轮研究院,四川江油621703)
湍流燃烧模型在燃烧室数值模拟中的对比分析
刘重阳,戴斌
(中国燃气涡轮研究院,四川江油621703)
以某单头部矩形燃烧室为研究对象,采用多种湍流模型和燃烧模型进行组合计算,模拟燃烧室内部的速度场和温度场,并对计算结果进行对比分析。结果表明:湍流模型主要影响火焰筒内部主燃孔横截面上游的速度分布,Standardk-ε和Realizablek-ε模型的速度场计算结果差异相对较小;湍流动能预测受湍流模型的影响较大,并具有一定规律性;不同组合模型对燃烧室内部和出口温度分布的局部细节模拟差异较大,燃烧模型影响最大;PDF模型计算的温度值较合理,另外三种燃烧模型在单步完全反应燃烧机理下的计算值偏高,计算获得的OTDF也相差较大。
航空发动机;燃烧室;数值模拟;温度场;湍流燃烧模型
1 引言
随着计算机技术和计算燃烧学的迅速发展,燃烧室数值模拟技术也不断提高。湍流燃烧模型作为一种基本燃烧模拟工具一直受到广泛关注,其选择是否合适对计算结果有很大影响。到目前为止,已经研究和发展了不同的湍流燃烧模型,总的趋势是寻找更为合理的计算方法,但缺乏令人满意的、能同时满足工程应用中合理性和准确性的模型[1]。
许多学者对湍流燃烧模型在航空发动机燃烧室数值模拟中的应用进行了对比分析。郭尚群对Standardk-ε模型和RNGk-ε模型进行比较,得出RNGk-ε模型略优于Standardk-ε模型[2]。金戈等在FLUENT软件中采用非预混概率密度函数(PDF)燃烧模型,对Standardk-ε模型、RNGk-ε模型及Realizablek-ε模型进行对比,确定Realizablek-ε模型适合燃烧室数值计算[3]。Jiang等在FLUENT软件中采用层流小火焰燃烧模型,以2D某单管燃烧室为研究对象,对Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型、Standardk-ω模型、剪切应力输运模型(SST)和雷诺应力模型(RSM)进行比较研究,得出RSM模型优于其他湍流模型的结论[4]。Mongia在其文中提到:Giridharan对DACRS混合器流场计算的最新研究表明,FLUENT的Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型和RSM模型中,Realizablek-ε模型的预测结果与试验结果最吻合;Hsiao等模拟的旋流杯流场中,Standardk-ε湍流模型的预测结果最好[5]。
由此可见,目前燃烧室数值模拟中采用的湍流模型并不统一,对其进行的诸多对比分析研究结论也不一致,未形成统一的参考标准;对于燃烧模型,研究者也是各持观点,采用的计算方法不一。本文采用FLUENT软件,以某模型燃烧室为研究对象,对软件中的四种湍流模型和四种燃烧模型进行计算分析,对比其在预测燃烧室内部速度场和温度场上的差异,以期为湍流燃烧模型在该类型燃烧室数值模拟上的工程应用提供参考。
2 计算模型及方法
2.1 建模及网格划分
某单头部矩形燃烧室,其头部为双级轴向旋流器结构,火焰筒为传统的气膜冷却结构,如图1所示。建模时,在不影响整体流场的前提下,简化局部细节(如喷嘴、点火电嘴等);增加出口通道长度以便于收敛;模型坐标原点位于突扩扩压器进口中心,其中X轴与旋流器轴线重合。采用非结构化四面体网格,在头部和火焰筒小孔等参数梯度变化较大的区域进行网格加密,网格单元总数约264万。
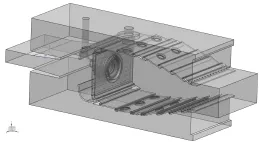
图1 燃烧室计算流体域几何模型Fig.1 The geometrical model of combustor fluid domain
2.2 边界条件和计算方法
为比较不同湍流模型和燃烧模型计算结果差异,采用表1所示模型组合计算,共计11组。表中,FR/ED为有限速率/涡耗散模型,ED为涡耗散模型,EDC为涡耗散概念模型。计算参数为:进口空气流量0.973 5 kg/s,总压550 kPa,总温600 K,余气系数2.5。进口边界给定流量、总温、湍流强度和水力直径;出口为自由流出口;壁面绝热无滑移。
为避免壁面附近区域网格过细,近壁区域模拟采用标准壁面函数;选用离散相DPM模型模拟燃烧室内两相流动;采用P1模型模拟辐射换热。燃烧模型中,PDF模型选用16组分简化化学反应机制,另外三个采用替代燃料C12H23的单步完全反应模拟。控制方程采用一阶迎风格式离散,压力-速度耦合采用SIMPLE算法,同时采用亚松弛因子控制收敛。

表1 计算选用的湍流模型和燃烧模型Table 1 The turbulent models and combustion models applied in the simulation
3 计算结果与分析
3.1 速度场对比
11组模型计算得出的速度场结构基本一致,只是在回流区大小和主燃孔射流穿透深度上稍有差别。图2给出了模型中心纵截面速度矢量场的部分计算结果。
图3为11组模型燃烧区中心线(从喷嘴出口中心至燃烧室出口中心)上轴向分速度(U速度)沿X轴的变化曲线。可见,各模型计算的中心回流区尾缘在轴向上的位置,均位于主燃孔中心横截面(X= 185.137 mm)处,但回流区和文氏管内的U值大小、气流回流至上游的位置各不相同:①在旋流器出口上游文氏管内,Realizablek-ε+PDF、Standardk-ε+ PDF和Standardk-ε+ED模型计算的U值明显大于其他模型,文氏口附近数值上相差最大约90 m/s;在旋流器出口至主燃孔中心横截面之间,RNGk-ε+ PDF和RSM+PDF模型计算的U值明显大于其他模型,回流区边缘与主燃孔大股射流交界处数值上相差最大约70 m/s。②Standardk-ε+FR/ED、RSM+ FR/ED、RSM+ED和RSM+EDC模型,在主燃孔中心横截面之前计算的U值均为负值,即回流区气流均回流至喷嘴出口处,其他模型则是回流至旋流器出口或接近喷嘴出口处。随着气流向下游流动,除RNGk-ε+FR/ED模型计算结果明显较低外,其余各模型计算的U速度基本无差异。
图4为各计算模型燃烧区不同横截面上平均流速沿X轴的变化曲线。可见,所有模型的速度变化趋势相同,在主燃孔和掺混孔中心(X=239.258 mm)横截面附近都出现两次速度波动,这主要是由于主燃孔和掺混孔气流冲击形成回流所致。在掺混孔横截面之前,RNGk-ε+PDF模型预测的截面平均流速最大,Realizablek-ε+PDF模型的最小,两者最大相差约20 m/s;掺混孔横截面之后,截面上的平均流速随流动距离的增加而增大,至燃烧室出口处达到最大,各模型计算结果的差异也随之减小。

图2 中心截面速度矢量图Fig.2 The velocity vector graph of center section

图3 燃烧区中心线上轴向分速度沿X轴的变化曲线Fig.3 The axial velocity changes of centerline alongXaxis

图4 火焰筒内横截面平均速度沿X轴的变化曲线Fig.4 Average velocity changes of the cross section alongXaxis
图5为采用相同湍流模型时不同轴向位置处平行于Y轴的直线上的U速度分布,从图中可看到气流速度沿轴向在径向上的变化过程及回流区径向边界(U=0)。采用Standardk-ε和Realizablek-ε模型时,不同燃烧模型计算结果显示,仅在旋流器出口附近(X=145 mm处)略有差异,其余位置基本相同;采用RNGk-ε模型时,FR/ED和PDF模型计算结果差异较大,主要体现在速度大小和回流区边界上;采用RSM模型时,在掺混孔中心横截面之前,PDF模型计算结果与FR/ED和PDF模型相比差异明显,ED模型在X=165 mm位置之前略有偏差。对比回流区径向边界,图5(a)、(c)、(d)均显示回流区径向最大尺寸,基本位于X=165 mm、Y=±20 mm点上,而RNGk-ε模型结果显示的尺寸略小。

图5 不同轴向位置轴向分速度的径向分布Fig.5 The radial distribution of axial velocity at different axial position
图6为11组模型燃烧区中心线上的湍流动能k沿X轴的变化曲线。可见:在旋流器出口截面以后,湍流动能计算值的规律是Realizablek-ε模型>Standardk-ε模型>RSM模型>RNGk-ε模型,且与燃烧模型无关;在旋流器出口截面之前的文氏管流道内,此规律不明显。在主燃孔和掺混孔中心横截面处,湍流动能达到最大峰值。Realizablek-ε模型计算所得湍流动能最大,这是因为此湍流模型的湍流粘度计算公式中,引入了与旋转和曲率有关的内容,且方程中的产生项不再包含k方程中的产生项。
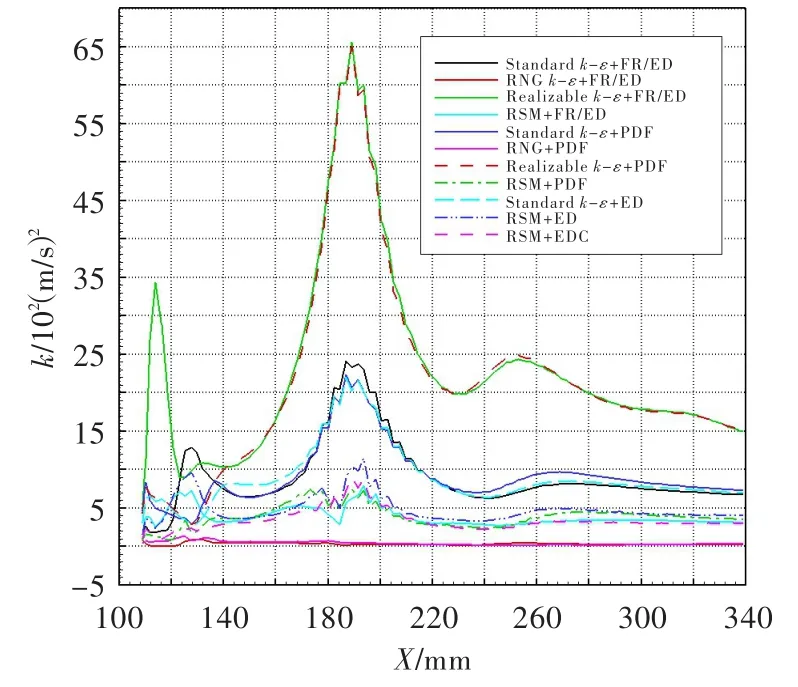
图6 中心线上湍流动能沿X轴的变化曲线Fig.6 The turbulent kinetic energy changes of centerline along Xaxis
11组模型计算的旋流器通道内部的有旋流动和中心回流区内的大分离流动结果差异较大,主要是因为四种湍流模型在求解湍流动能方程和耗散率方程上存在区别[6]:Standardk-ε模型先求解湍流动能方程和耗散率方程,然后再计算湍流粘度;RNG k-ε和Realizablek-ε模型均对耗散率方程进行了改善,前者通过在大尺度运动和修正后的粘度项中体现小尺度影响,后者增加了一个为层流速度波动而作的耗散率传输方程,在时均应变率特别大时需对某种正应力进行某种数学约束;RSM模型放弃等边性边界速度假设,考虑了各向异性效应,直接求解N-S方程中的雷诺应力项,同时求解耗散率方程。
此外,各种湍流模型都有一定的局限性,部分系数需要靠经验来确定。这是因为在构造模型时对许多未知项知之甚少,有很多量至今没有直接的测量数据作参考,所作的假设主观臆测程度较大,尤其表现在ε的模拟方程中。同时,由于不少湍流模型与涡粘性概念相联系,因而涡粘性假设本身的不真实性必然影响到模型的精确性。
3.2 中心温度场对比
图7~图9为各组模型计算的燃烧室中心截面总温分布云图。总体看,各模型计算火焰筒内燃烧高温区分布大体一致,高温区基本上集中在回流区,及主燃孔和掺混孔之间,但仔细对比又有些不同。
图7中,在文氏管出口区域,RSM模型计算有高温燃气;在挡溅板与火焰筒交接处的角落回流区,RNGk-ε模型计算的温度最低,Realizablek-ε和 RSM模型计算值相对较高;Standardk-ε模型计算的高温燃气区位于主燃孔后的卷吸区,Realizable k-ε模型位于主回流区和上下两个角落回流区内,RSM模型位于主回流区内,RNGk-ε模型计算的高温燃气区面积最小且上下分布不对称。
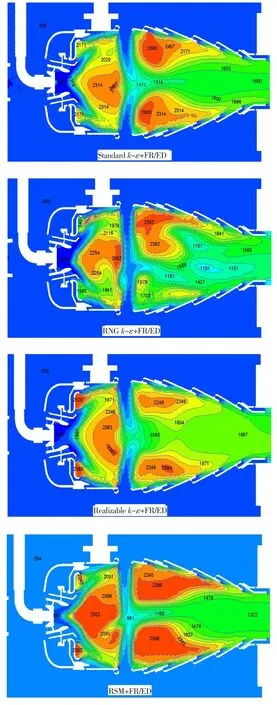
图7 采用FR/ED模型的燃烧室中心纵截面总温分布Fig.7 The total temperature distribution of center section applying FR/ED model
从图8中可以发现,4种湍流模型的结果均显示有高温燃气回流至旋流通道内,Standardk-ε和Re⁃alizablek-ε模型的回流深度更大。与图7相比,4种湍流模型在主回流区和角落回流区的预测温度都相对较低。与理论温度值相比,PDF模型的计算结果相对较合理。
与图8相比,图9中3种湍流模型的高温燃气分布更清晰,分布区域略大;与图7相比,图9中除数值上略高外,其余相差不大。
图10、图11为燃烧室中心线和不同横截面上总温沿X轴的变化曲线。可见,各组模型计算的温度分布趋势大体一致,但数值上差别明显。最大值差异主要体现在掺混孔上游区域内,中心线上最大值与最小值相差约750℃,横截面上最大值与最小值相差约350℃。即使采用相同湍流模型,差异也如此。
由此可见,燃烧模型对燃烧室内温度场的计算结果影响最大。对于CFD数值模拟,模型推导方法和燃烧机理不同,必然导致不同的模型常数、温度场求解变量和附加函数,以及k和ε输运方程中出现不同的附加项,从而使得模型的模拟结果不同。

图8 采用PDF模型的燃烧室中心截面总温分布Fig.8 The total temperature distribution of center section applying PDF model

图9 采用ED和EDC模型的燃烧室中心截面总温分布Fig.9 The total temperature distribution of center section applying ED and EDC model

图10 中心线上总温沿X轴的变化曲线Fig.10 The total temperature changes of centerline alongXaxis
3.3 出口温度分布对比
各组合模型计算的燃烧室出口截面的总温分布差异较大:Realizablek-ε模型的高温区最集中,位于出口中心稍偏下,其余模型的高温区相对较分散;所有组合计算的出口温度各不相同。
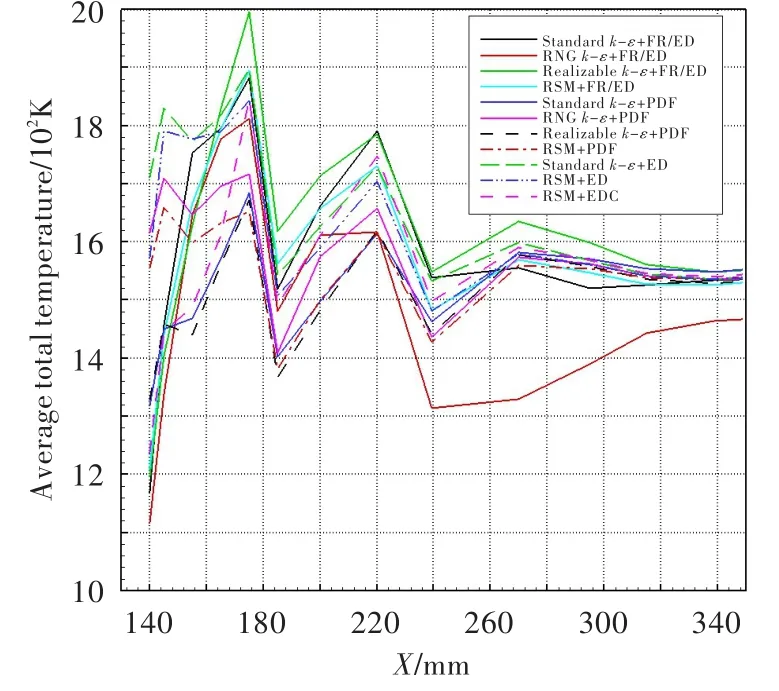
图11 火焰筒内各截面平均总温沿X轴的变化曲线Fig.11 Average total temperature changes of different section alongXaxis

图12 燃烧室出口径向温度分布Fig.12 The radial temperature distribution of combustor outlet

表2 燃烧室出口总温及OTDFTable 2 The total temperature of combustor outlet and OTDF
4 结论
(1)各组合模型计算的总体流动差别较小,但局部细节差异较大。不同湍流模型对于旋流器通道内部有旋流动和中心回流区内大分离流动的计算结果差异较大,主要体现在气流速度大小和回流区边界上。燃烧模型和不同湍流模型组合计算时,在速度场预测上差异程度也有所不同,与Standardk-ε和Realizablek-ε组合的所有模型的计算结果差异相对较小。
(2)火焰筒内部湍流动能受湍流模型的影响较大,并有一定的规律性,数值上Realizablek-ε模型>Standardk-ε模型>RSM模型>RNGk-ε模型,燃烧模型对湍流动能的影响不明显。
(3)11组模型对于燃烧室内部及出口温度分布模拟存在差异,燃烧模型的影响最大。与理论值相比,PDF模型的温度较合理,FR/ED、ED和EDC模型在单步完全反应燃烧机理下的计算值偏高。
(4)目前,由于缺少试验数据验证,根据本文计算结果仅能分析出模型间的差异,而无法做出合理性和准确性判断,接下来还需要在试验验证方面多开展研究工作。
[1]吴超.湍流燃烧模型在燃烧室数值计算中的应用研究[D].沈阳:沈阳航空工业学院,2009.
[2]郭尚群,赵坚行.环形燃烧室两相燃烧流场的数值模拟[C]//.中国工程热物理学会2004年学术会议论文集.辽宁大连:中国工程热物理学会,2004:322—327.
[3]金戈,张志学,顾铭企.QD128航改燃气轮机燃烧室数值模拟[J].航空发动机,2008,34(2):30—35.
[4]Jiang L Y.A Critical Evaluation of Turbulence Modeling in a Model Combustor[R].ASME GT2012-68414,2012.
[5]Mongia H C.Recent Progress in Comprehensive Modeling of Gas Turbine Combustion[R].AIAA 2008-1445,2008.
[6]蒲宁,徐让书,吴超,等.航空发动机燃烧室流动数值计算中湍流模型的比较[J].沈阳航空工业学院学报,2008,25(5):24—27.
Comparison and Analysis of Turbulent Combustion Models in Numerical Simulation of Combustor
LIU Chong-yang,DAI Bin
(China Gas Turbine Establishment,Jiangyou 621703,China)
The inner velocity and temperature fields of a single-dome rectangular combustor were simulat⁃ed with various turbulence models and combustion models.Through comparison and analysis,it is found that the turbulence models are the main influential factor on the velocity distribution before the cross sec⁃tion of primary hole,the difference of velocity field results between the Standardk-εmodel and the Realiz⁃ablek-εmodel is slight.The turbulence models mainly affect the turbulence kinetic energy and turbu⁃lence intensity,and the simulation results have a stated regularity.There is a big difference in the details of combustor inner and exit temperature distribution applying different combined models,the combustion mod⁃els play an important role in the result difference.The temperature value is simulated reasonably using PDF model,but the results got from the other three combustion models which used the global reaction mecha⁃nism are on the high side,theOTDFcalculated from the results also have many differences.
aero-engine;combustor;numerical simulation;temperature field;turbulent combustion model
V231.3
:A
:1672-2620(2014)05-0012-07
2013-10-07;
:2014-03-31
刘重阳(1980-),男,江苏徐州人,高级工程师,硕士,主要从事燃烧室数值模拟与试验技术研究工作。
