斐波那契数的标准分解式中因子19的指数

严婉琳

（华南师范大学 数学科学学院，广东 广州 510631）

斐波那契数的标准分解式中因子19的指数

严婉琳

（华南师范大学 数学科学学院，广东 广州 510631）

研究和探讨斐波那契数Fn标准分解式中因子19的指数与其下标n之间的内在联系，同时证明，斐波那契数Fn下标n的分解式中因数18的指数与19的指数，将一起决定Fn标准分解式中因子19的指数。

斐波那契数；标准分解式；因子；指数；同余

1 引言

斐波那契数列，又称为黄金分割数列，在现代物理等领域，斐波那契数列有着广泛的实际应用。多年来，学者们都对斐波那契数投以关注的目光。

定义1.1[2-3]斐波那契数列是指递推关系Fn=Fn－1+Fn－2（n≥2）所确定的数列{Fn}n≥2，这里的初始条件是F0=0，F1=1，并且Fn称为斐波那契数。

在查找关于斐波那契数的标准分解式中因子的指数相关文献的过程中，文献[4-10]已经研究了关于斐波那契数的标准分解式中因子2，3，5，7，11，13，17的指数，文献[11，12]则证明了斐波那契数的整除特征和整除性。此外，文献[13]不仅提出了一个关于一般奇素因子p在Fd（p）标准分解式中的指数的猜测，还研究了对一般奇素因子p与d（p）=min{w：p/Fw}的整除关系。本文则是在研究上述相关文献之后，得出了斐波那契数Fn下标n的分解式中因数18的指数与19的指数将决定Fn标准分解式中因子19的指数的结论。

引理1.1 如果m|n，则有Fm|Fn，这里假设m，n为正整数，记号“a|b”表示a整除b

引理1.2 假设m，n为正整数，则有Fm+n=FmnFn-1+ Fm+1Fn.

引理1.3 19|Fn⇔18|n，这里假设n为正整数。

根据斐波那契数的定义及相关数论知识，逐一计算Fn（0≤n≤17）关于模19的最小非负剩余，可得到以下结果：F0≡0（mod19），F1≡1（mod19），F2≡F1+F0≡1（mod19），F3≡F1+F2≡2（mod19），…若 设 Fn≡m（mod19），则可得表1。

表1 关于模19的最小非负剩余

因此可以得知，在斐波那契数列之中，Fn关于模19的最小非负剩余的周期是18，并且Fn≡0（mod19）当且仅当n≡0（mod18），即19|Fn⇔18|n

引理1.4 设m为正整数，F18m+1≡F18m－1（mod19）

证明 由引理1.3及斐波那契数的定义知道，F18m≡F18m+1－F18m－1≡0（mod19），故引理1.4成立。

引理1.5 设m为非负整数，i是通过模18的最小非负剩余系，则F18m+i≡Fi（mod19）

证明 当i=0时，由18|18m及0|18可知F18m≡F0（mod19），所以结论成立；当i≠0时，由引理1.2及引理1.3可知，F18m+i=F18mFi－1+F18m+1Fi≡F18m+1Fi≡Fi（mod19）.

引理1.6 设m，p为正整数，则

假设a，b是整数，t是非负整数，那么记号at||b，即at|b的含义是b恰好可以被a的t次方整除，但b不可以被at+1整除。

2 相关证明

定理2.1 假设p和k都是正整数，则有F18kp与F18k+1p标准分解式中因子19具有相同的指数。

证明 由引理1.3可以得到19|F18kp，假设n=18kp，s（s≥1）且p是一个正整数。因为在F18kp标准分解式中，因子19的指数必定是大于0.要证得定理，可以利用数学归纳的方法。

（i）当k=1时，若s是F18kp的标准分解式中因子19的指数，即19s||F18p，下证19s||F182p.

由于18p|182p，由引理1.1知F18p|F182p，从而有F182p≡0（mod19s

）另一方面，令m=18p，则由引理1.6可知，F18×18p≡，进而由及2s≥s+1可得

再由引理1.4知，F18m+1≡F18m－1（mod19），从而，并且19不能整除，故19s+1不能整除F182p，所以，即当k=1时，F18kp与F18k+1p标准分解式中因子19具有相同的指数。

（ii）假设k≥1时，F18kp与F18k+1p标准分解式中因子19具有相同的指数s（s≥1）。

此后需要证明在k+1的情形下，结论也是成立的，即证明F18k+1p与F18k+2p的标准分解式因子19的指数也为s.

因为18k+1p|18k+2p，由引理1.1得到F18k+1p|F18k+2p从而有F18k+2p≡0（mod19s）另一方面，令m=18k+1p，则由引理1.6知

再由引理1.4知F18k+1p+1≡F18k+1p－1（mod19），从而

定理2.2 假设p为一个不含18和19的正整数，则1是F18p的标准分解式中因子19的指数。

证明 已知18|18p，由引理1.1有F18|F18p，从而有F18p≡0（mod19），下证F18p不能被192整除。不妨设p= 19m+r，1≤r≤18，则

借助计算机实现可得到192||F18×19，从而F18p≡F18×19m+1F18r（mod192）

又192不能整除F18r（1≤r≤18），且19不能整除F18×19m+1，从而192不能整除F18×19m+1F18r，即192不可以整除F18p，因此得到19||F18p，所以1是F18p的标准分解式中因子19的指数。

下面定理2.3的证明，可以使用上述方法。

定理2.3 假设p为一个不含18和19的正整数，则2为F18×19p的标准分解式中因子19的指数。

定理2.4 假设n=18×19sp，同时假设s是任意一个非负的整数并且p是不含18和19的一个正整数，则s+1是F18×19sp标准分解式中因子19的指数。

证明 为了证明对于因子19的指数在n的分解式中应用，可以利用数学归纳方法来证明。

（i）s=0时，n=18p，从定理2.2知，s+1=1是F18p标准分解式中因子19的指数，所以s=0时，结论显然成立。

（ii）s=1时，n=18×19p，从定理2.2可以得知，s+1=2是F18×19p标准分解式中因子19的指数，因此s=1时，结论也显然成立。

（iii）首先作出假设，即这个命题对于s≥1都显然成立，即F18×19sp的标准分解式中因子19的指数为s+1，下证F18×19s+1p的标准分解式中因子19的指数为s+2，即

令m=18×19sp，由引理1.2有

由（1）～（5）式可得

当s≥1时，有2（s+1）≥s+3，则由引理1.4及18|m知，Fm+1≡Fm－1（mod19）且其最小非负剩余不是0，代入式（6）得

从而由19s+1得到即

下证19s+3不能整除

首先由式（7）有

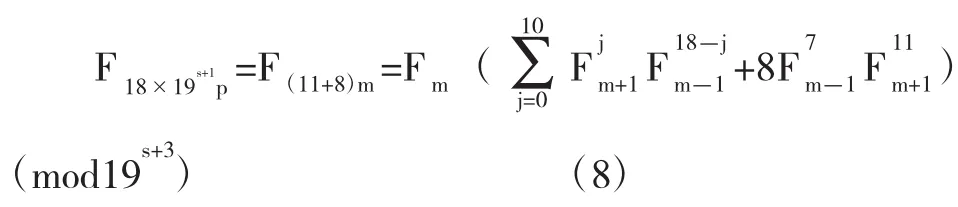
要证19s+3不能整除，由，只需证192不能整除.由引理1.4及表1不妨设Fm+1=19q1+r，Fm－1=19q2+r，这里r=1，q1，q2为非负整数，从而

因为19s+1||Fm=Fm+1-Fm－1=19（q1-q2），所以19s||（q1-q2）.又r+143q1+199q2≡r+10（q1-q2）（mod19）知，19不能整除r+143q1+199q2.且（r，19）=1，则（r17，19）=1，由式（9）知192不能整除

再由式（8）知，19s+3不能整除，故，即在标准分解式中因子19的指数是s+2=（s+1）+1.

因此定理2.4显然成立。

结合上面已经得到的定理及其证明，我们可以得到如下结论，即定理2.5.

定理2.5 假设n为一个正整数，n=18k×19s×p，k，s都是非负整数，而p是一个不含因数18和19的正整数，则有

1）当k=0的时候，Fn标准分解式中因子19的指数是0；

2）当k≥1的时候，Fn标准分解式中因子19的指数是s+1.

证明 1）k=0的时候，由于n不可以被18整除，根据引理1.3可得知，0是Fn标准分解式中因子19的指数，因为19不可以整除Fn.

2）k≥1时，由定理2.1知，F18kp标准分解式中因子19的指数与F18k+1p准分解式中因子19的指数是相同的，所以只需要考虑k=1的情形。

根据定理2.4可以得知，s+1是F18×19sp标准分解式中因子19的指数。最终，定理2.5得证。

[1]曹汝成.组合数学[M].广州：华南理工大学出版社，2006：91-98.

[2]潘承洞，潘承彪.初等数论[M].2版.北京：北京大学出版社，2003.

[3]吴振奎.斐波那契数列[M].沈阳：辽宁教育出版社，1987：43-152.

[4]袁明豪.正Fibonacci数的标准分解式中因子2的指数[J].数学通讯，2003，（15）：26-27.

[5]袁明豪.正Fibonacci数的标准分解式中因子3的指数[J].荆州师范学院学报：自然科学版，2003，26（2）：12-13.

[6]袁明豪.正Fibonacci数的标准分解式中因子5的指数[J].数学的实践与认识，2007，37（7）：166-170.

[7]王念良，张洁.Fibonacci数的标准分解式中因子7的指数[J].商洛学院学报，2007，21（4）：4-7.

[8]林丽荣，尤利华.Fibonacci数的标准分解式中素因数11的指数[J].甘肃联合大学学报，2008，22（6）：4-10.

[9]黄荣辉，尤利华.Fibonacci数的标准分解式中素因数13的指数[J].江西师范大学学报，2012，36（3）：234-237.

[10]林伟芬，尤利华.Fibonacci数的标准分解式中素因数17的指数[J].淮阴师范学院学报，2013，12（3）：213-217.

[11]袁明豪.Fibonacci数的一组整除特征[J].数学通讯，2004，（15）：29-31.

[12]吴佃华，贾小英.Fibonacci数的整除性[J].广西师范学院学报，2007，24（3）：28-29，60.

[13]尤利华，黄荣辉.Fibonacci数的标准分解式中诸奇素因数的指数[J].广西师范大学学报，2011，29（3），18-22.

G642.0，O156

A

1674-9324（2014）42-0225-04