数字图书馆联盟中概率数据集成系统上的top-k查询
2014-02-27潘林
潘 林
(青岛港湾职业技术学院 山东 266404)
0 引言
数字图书馆是虚拟的图书馆,其目的是在网络环境下构建共享的可扩展的知识网络系统,提供超大规模的,分布式异构数字化信息的智能检索和服务的知识中心[1]。
由于单一的数字图书馆提供的资源有限,不能满足每个用户的访问需求,所以理想的方式是为用户提供可以一次请求访问多个数字图书馆资源的途径。于是人们提出了联盟数字图书馆(Digital Library Federation简称DLF)的概念[2]。
在一个数据集成的系统中,一个查询在中介模式上提交后,查询会产生若干带有概率的重写形式。这样结果中的每个元组都会具有不同的概率,我们可以采用 top-k算法来获得最近似的k个结果。在一个DLF中,最终用户会希望获得结果中最符合其偏好且概率最高的结果。这样,在传统的 top-k算法中,需要同时考虑依据偏好形成的得分函数与概率直接的关系。
1 数字图书馆联盟DLF的概率的信息集成模型
Lenzerini 等[3]提出了一种数据集成的理论模型,基于该模型,本文定义了概率性的数据集成模型,其形式化描述如下:
一个数据集成系统Δ 是一个四元组
其中G是全局模式,用使用了一组相关字母表Ag的逻辑理论来表达
S是源数据的模式,用使用了一组相关字母表As的逻辑理论来表达
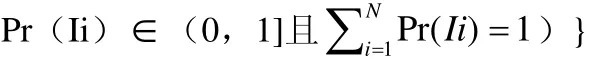
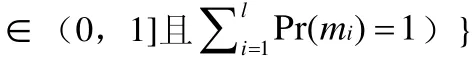
对于映射mi∈M来说,我们可以定义为属性的对应关系,一个属性对应可表达为Cij=(Si,Ti),其中Si是模式S中一个源属性,Ti是模式T中一个目标属性。
在图书馆联盟中,由于每个DL的自治性,适于利用LAV表达映射关系,其形式化描述为:
∀ x( s( x) → qg( x ))当qg⊇s时
∀ x( s( x) ≡ qg( x ))当 g≡qs
∀ x( q g( x) →s( x ))当s ⊇ qg时
其中s是S的一个元素,gq 是在G上一个查询。
2 模式映射的概率
2.1 映射的概率
在进行模式的自动映射时,可能会产生几种候选的模式对应关系,每一种都有其出现的概率,其元组的概率分布情况分为两类:
(1)在所有的数据上会采用一种相同的映射关系,称为by-table 映射,这是本文所关注的。
(2)在源数据的关系中,会出现多个元组的子集采用不同的映射关系 称为by-tuple映射。
2.2 查询
当从G上提交查询时,会按照各种映射形式形成多个查询的重写形式,对于每个返回的结果,其概率是不同的。
对于在G上的一个查询Q,按照其与某个局部模式S可能会有的映射形式,可重写成 Q….Q,对于 Q( i ∈ [1,k])中的元组 t∈ans( Q),t有如下形式 t={t1,….tj}, t1∈ R,… t j ∈ R, R( λ∈[1,j])为与t相关的具有概率的关系模式,我们定义与t相关的布尔表达式:
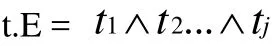
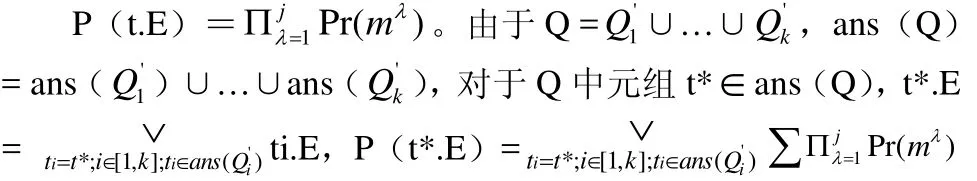
即Q的查询结果中每个元组的概率为包含该元组的查询重写的概率之和。
根据计算,我们得出如下的图示:

图1 概率
3 Top-k 查询回答
3.1 U-kRanks查询的定义
以下是对U-kRanks的定义:
D为一个具有可能的实例集I= {I1,I2,….In}的概率数据库,且∑r(Ii)=1。对于i=1….k,让{ t,… t}为一个元组集,其中每个元组会在一个非空的实例I()中根据得分函数F出现在位置i。一个在F上的U-kRanks查询,会返回结果{ t*; i=1….k},其中
3.2 状态的概率的定义
假定以得分函数F访问一个数据库D,在访问了m个元组后,这些元组会形成若干个状态,设sm,l为其某个状态,其中l(l<=m)个元组出现在该状态中,表示为sl,未出现的(m-l)个元组表示为 Im,则状态 sm,l的概率为 ρ(sm,l)=Pr(sl∩ ls¬),例如假若已经检索出的元组为{t1,t2,t3,t4},对于其中某个状态s(4,3)=
3.3 利用状态树对opt_U-kRanks算法的讨论
首先本文采用树结构来阐述opt_U-kRanks查询。假设得分排序的元组向量为(t1,t2....tn)(见图1),每个节点代表一种具有一定概率的状态,其值代表了该状态的长度,即位次。节点i和j组成的边表明通过添加一个新的元组状态(出现或不出现),状态i可以变成另一个状态j。形如t1t2....ti的从根节点到一个非根节点i的路径正好表达了状态i。
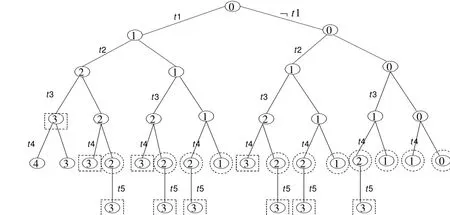
图2 状态数
如图1表示了位置(rank)为3,当前元组集为{t1,t2,t3,t4}时的状态图,根到虚线矩形内的元素形成的路径为符合要求的状态集即{t1,t2,¬t3,t4}{t1,¬t2,t3,t4}{¬t1,t2,t3,t4},新加入的元组可在剩余的路径中形成符合要求的状态集(即根到虚线椭圆内元素形成的路径)
当新元组t5后,位置(rank)为3时符合要求的状态都是从根到虚线椭圆内元素形成的路径集合中选择子集加入新元素(元组t5)后形成的
正如图2描述,虚线矩形内的节点表示了排序元素个数为3的状态,椭圆内节点表示了加入元组t4后排序元素个数小于3(包括0,1,2)的节点。从图中可以看出,只有在长度为i-1的状态上添加元组t才能保证其出现在排序i上。这时我们可以计算t4按照排序函数出现在位置3的概率为:

根据图1,我们可以推到一个可使计算快速收敛的不等式。
对于位置k,由于任何一个事件的概率都不会大于1,所以在图1中有 P5,3<= S= ∑ ρ(s4,2)。
不失一般性,对于任意元组 tm,不等式 Pm,k<= S=∑ρ(sm−1,k−1)(k is a rank position)都是成立的。如果我们要求tm为在排序位k时的概率,我们应该保证,mkP 是所有的里面最大者。从前面的讨论,我们也可以推断出即使用如所提出的Pm,k> S代替 Pm,k> Pm+1,k的方案,也不能保证 Pm,k比 Pm+2,k'or....or,nkP (n>i)大。下面,我们来简化该不等式。
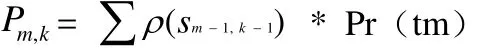
如图1所描述的,我们有:

当k>=2时,我们有:
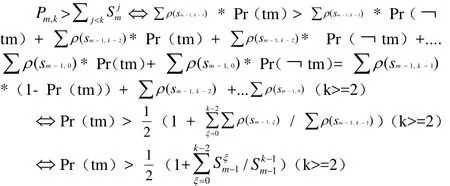
当k=1时,我们有:

综上,我们可以得到一个近似的条件,即Pr(tm)>= 1/2,该条件可快速评估tm是否是在位置上的适合的解。
[1]E.A.Fox.Source Book on Digital Libraries.Technical Report TR-93-35 Virginia Polytechnic Institute and State University,1993.
[2]S.P.Harter.W hat is a Digital Library? Definitions,Content,and Issues.In KOLISS,1996.
[3]Birm ingham B.,et al.EU-NSF digital library working group on interoperability between digital libraries.http://www.iei.pi.cnr.it/DELOS/NSF/interop.htm,2001-10-15.
