基于软阈值和遗传自适应阈值的车辆制动信号的联合小波去噪*
2014-02-27贺岩松徐中明张志飞
贺岩松,刘 程,徐中明,张志飞
(1.重庆大学,机械传动国家重点实验室,重庆 400030; 2.重庆大学机械工程学院,重庆 400030)
前言
由于测量的车辆声信号一般会受到噪声污染,因此对车辆声信号进行声学分析前,首先要对其进行前处理。采用滤波器进行低通抗混叠滤波的传统方法只是保留低于截止频率的信号,而对高于截止频率的信号直接置零[1],这种处理没有根据信号的本身特点进行滤波,不利于信号的后续处理。当前广泛应用的小波去噪,由于其具有多分辨率特点,可以聚焦到信号的任意细节进行处理,频率分辨率可随频率变化自动调节,非常适用于非平稳信号的去噪,但标准的小波软阈值去噪方法也不能根据信号本身的特点选择最优阈值[2-5]。自适应阈值去噪算法能够根据信号的本身特点确定最优阈值,但其算法的迭代步长一般很难确定[6]。遗传算法具有很好的最优值搜索特性,通过遗传迭代可以得到最优解,但其计算速度随数据量的增加而变慢[7]。一般车辆车内声信号的能量主要集中在低频段上,因此可以在保证精度的基础上对信号的高频小波系数进行软阈值去噪,对低频小波系数进行新的阈值去噪。本文中在对自适应阈值去噪算法分析的基础上,利用遗传算法对该方法进行改进,提出了一种适用于车辆声信号的联合小波去噪方法,为声信号的后续处理奠定基础。
1 小波阈值去噪的基本思想
一维含噪信号模型[1,7]可表示为如下形式:
yi=xi+ni(i=0,1,…,Nn-1)
(1)
式中:xi为原始信号;ni为方差为σ2的高斯白噪声;Nn为信号数据点数。
离散小波阈值去噪基本过程如图1所示。基本思想为对小波分解后的各层小波系数中模值大于和小于某阈值的系数分别处理,然后对处理后的小波系数再进行反变换,重构出经过去噪后的信号。其中,关键是阈值的选取和如何对小波系数进行量化。
标准的软阈值估计函数定义为
(2)
式中t(t≥0)为阈值。
标准阈值函数阈值的一般计算公式为
(3)
式中:nj为在尺度j上小波系数的长度;σj为噪声的标准方差,当噪声的标准方差未知时可用下式估计:
σj=median(|dj,k|)/q
(4)
式中:median(·)为求输入向量中间值函数;dj,k为第j层的小波系数;常数q在0.4~10之间取值,具体取值与实验数据有关,一般建议取值为0.674 5[8]。
2 基于遗传算法的自适应阈值去噪
2.1 自适应阈值去噪
在实际去噪过程中,须根据信号本身的特点对阈值参数进行修正,因此一些学者[6-7,9]应用均方误差(MSE)的估计来进行自适应阈值去噪,并根据均方误差的无偏估计推导出自适应阈值的优化迭代算法。其去噪过程如图2所示。
式(2)中,当t≥0时,均方误差MSE的期望函数定义为
(5)
一般用无偏估计JSURE来替换JMSE的估计,通过数值梯度算法来计算最优解topt。其第k步的迭代公式为
t(k+1)=t(k)+Δt(k)
(6)
(7)
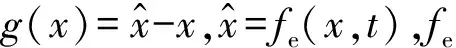
采用式(7)计算阈值梯度时,需要g(x)及其偏导数,但标准的软阈值去噪函数(式(2))不具有2阶可导,因此fe(·)选取一种新的软阈值函数fns(x,t),其定义如下[2]:
(8)
式中λ≥0为用户自定义参数。当λ>0时,fns(x,t)有高阶导数;当λ=0时,fns(x,t)为标准的软阈值函数。
x取值为[-3,3],t取值由式(3)和式(4)确定,λ取不同值时fns(x,t)对应曲线如图3所示。由图可见,λ=0.2和λ=0.8时的两个阈值函数和λ=0时的标准软阈值函数相差无几,因此可以预期新的阈值函数可取得较好的去噪效果。本文中选取λ=0.8,此时g(x),∂g(x)/∂t和∂2g(x)/∂x∂t对应值如图4所示。
2.2 遗传算法自适应阈值去噪
当应用自适应阈值算法进行迭代求解最优值时,迭代的收敛速度往往很慢或优化的结果并不能满足精度要求,因此选择合适的步长矩阵α(k)来迭代搜索最优适应阈值十分困难。为解决以上问题,文献[7]中提出了一种采用二进制代码的遗传算法(GA)来改善自适应阈值的迭代算法。由于遗传算法根据计算适应函数值进行评价,然后经过交叉和互换,得到子代种群,因此遗传算法比较容易搜索到局部最优值,一般把遗传算法的结果作为初始点,应用Matlab中的fmincon函数进行全局最优值搜索。
遗传算法的适应度函数[9]定义为
(9)
式中Δt(k)可由式(6)~式(8)计算得到,当梯度Δt(k)最小时,适应度函数也达到最小,可以认为t(k)=t(k-1)+Δt(k)达到最优化值。
遗传算法的输入参数设置如下:初始种群的大小设定为np=50;交叉概率为pc=0.7;变异概率为pv=0.1;最大的进化代数为Ng=50;q取0.8~5,利用式(3)和式(4)算出初始种群的范围为as;q取0.4~10,利用式(3)和式(4)得到最优值的搜索范围为aopt。基于遗传算法的自适应阈值去噪的计算流程图如图5所示。
3 遗传算法自适应阈值去噪和标准软阈值去噪方法的对比
3.1 去噪效果的评价参数
去噪效果的评价参数主要有均方误差Mse和输出信噪比Snrout,分别定义为
(10)

3.2 试验验证
选取Matlab中的Blocks、Bumps和Doppler等3种模拟噪声信号,信号的长度取为1 024点,采样频率为10kHz,它们都受信噪比分别为2、4、8、16的高斯白噪声的污染。选取小波基为db8,进行3层小波分解,对其分别采用一般的小波去噪和基于遗传算法的自适应阈值去噪。
图6~图8为受输入信噪比Snrin=16的高斯白噪声的污染后去噪前后的信号图,每幅图中依次是原始信号(C)、染噪信号(N),小波软阈值函数去噪信号(W)、遗传小波去噪信号(G)(即为遗传算法的自适应去噪信号)。可以看出,两种去噪结果的幅值平直区域都出现了起伏现象,但是遗传小波去噪信号在波形上更加逼近真实信号,因此这种改进的去噪方法比直接的小波去噪更好。两种方法去噪后评价参数结果见表1,可以看出遗传小波去噪的效果比一般的小波去噪好。

表1 两种去噪方法评价参数的结果对比
4 车辆制动声信号的软阈值函数与遗传自适应阈值的联合去噪
4.1 车辆声信号的特征分析
本文中分析的为某混合动力城市客车制动过程中车厢内驾驶员耳旁处采集到的声信号,采样频率为50kHz。通过Matlab中的Welch经典谱分析方法对信号进行谱分析。声压和功率谱随时间变化如图9所示,可以看出,在低频段功率谱随频率的增大而衰减较快,其声压级也较高,在较高频率段功率谱衰减缓慢。为进一步分析该车辆声信号的特征,采用小波变换和谱估计相结合的方法。利用Matlab中的db8小波基对车辆声信号进行6层小波分解,如图10所示,其中a1,a2,a3,a4,a5和a6分别为1~6层的低频部分的小波系数,d1,d2,d3,d4,d5和d6分别为1~6层的高频部分的小波系数,图中第1、3列为各层小波声压随时间变化曲线,第2、4列为该频段内的功率谱随频率变化曲线。具体小波分解每层频带如表2所示。
根据各层小波系数频率的分布范围,由图10可以看出,该车辆声信号为低频窄带噪声,能量主要集中在低频段,高频分量的幅值较小。在1~3层的分解中声信号的能量主要集中在低频部分,说明1~3层高频能量分布较少,信号的能量主要集中在3 000Hz以内;当信号分解到4~6层时,幅值-时间分布图上,低频段的波形基本不变,但高频段的波形幅值增大;在功率谱-频率分布图上,低频分量的衰减减缓,高频分量的增长减缓,尤其在第6层,低频段的能量和高频段的总能量基本趋于一致,因此4~6层的高频小波系数对信号的影响比较大。由小波分解理论可知频率段越高对应小波系数的长度就越长,进行阈值处理所需的时间越长[4-5]。1~3层高频小波系数能量分布较少,数据处理量比较大,可直接利用软阈值小波去噪;4~6层高频系数能量分布较多,并且数据量相对较少,利用遗传自适应阈值的小波去噪可以达到去噪的效果。

表2 频带分布表
4.2 针对车辆声信号的联合去噪应用
对该车辆声信号提出一种软阈值函数去噪和基于遗传算法的自适应阈值去噪的联合小波去噪方法,即利用阈值函数对1,2,3层高频小波系数进行去噪,用基于遗传算法的自适应阈值对4,5,6层的高频系数进行去噪。
利用软阈值去噪和基于遗传算法的自适应阈值去噪模块编写去噪程序,信号的长度为198 001点,采样频率为50kHz,遗传算法参数和软阈值去噪参数与上述相同,去噪前后信号的对比如图11和图12所示。图11为利用Matlab中的Welch方法对去噪前后进行功率谱估计对比,这种改进的去噪方法不仅保持了信号的低频部分,还对高频部分进行快速衰减;图12为对去噪前后信号的幅值-时间的局部放大图,可以看出去噪前后信号的基本波形没有改变,而去噪后信号的波动减小。说明通过改进的联合去噪方法可以达到很好的去噪效果。
5 结论
(1) 在对软阈值小波去噪和自适应阈值小波去噪对比的基础上,提出了基于遗传算法的自适应阈值去噪,并与软阈值小波去噪方法进行试验对比分析,验证了该方法的可行性。
(2) 对某车辆驾驶室内声信号进行小波分析和经典谱估计分析,表明该车辆声信号的能量主要集中在低频部分,在此基础上提出了基于软阈值去噪和基于遗传算法的联合去噪方法,试验结果对比分析表明该方法可以快速衰减高频噪声,减小信号的波动。
[1] 黄跃刚.FIR数字滤波器的MATLAB设计与DSP实现[D].沈阳:东北大学,2006.
[2] 邓玉娟.基于小波变换的语音阈值去噪算法研究[D].重庆:重庆大学,2009.
[3] 高玉华,王卫东,姜永胜,等.汽车振动信号去噪分析中的小波参数选择[J].合肥工业大学学报(自然科学版),2007,30(8):975-979.
[4] 雷英杰,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[5] 周伟.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006.
[6] Zhang Xiaoping. Thresholding Neural Network for Adaptive Nosie Reduction[J]. IEEE Trans.Neural Networks,2001,12(3):567-584.
[7] Li Jian, Cheng Changkui. Wavelet De-noising for PD UHF Signals Based on Adaptive Thresholding by Genetic Algorithm[C]. IEEE 2008 Annual Report Conference on Electrical Insulation Dielectric Phenomena,2008.
[8] Wang Y S. Sound Quality Estmation for Nonstationary Vehicle Noises Based on Discrete Wavelet Transform[J]. Journal of Sound and Vibration,2009,324:1124-1140.
[9] Nasri Mehdi, Nezamabadi-pour Hossein. Image Denoising in the Wavelet Domain Using a New Adaptive Thresholding Function[J]. Neurocomputing,2009,72:1012-1025.
