基于马尔可夫链的混合动力汽车行驶工况预测研究*

张 昕，王松涛，张 欣，田 毅

(1.北京交通大学机械与电子控制工程学院，北京 100044； 2.酒泉卫星发射中心铁路管理处，酒泉 732750)

前言

混合动力车辆在燃油经济性和排放性能方面的优势，来自于混合动力系统中两种动力源功率或转矩的合理分配。目前国内外的混合动力能量管理合理分配基本上均依赖于车辆当前时刻的行驶状态，如车速、需求转矩和蓄电池荷电状态(state of charge, SOC)等，没有考虑汽车未来的运行状态和驾驶员的预期功率需求，因此无法充分发挥混合动力汽车节能减排的潜力[1-2]。

汽车未来行驶状态具有较强的随机性和无后效性(即前一时刻的状态对下一时刻的行驶状态没有直接影响)，具有马尔可夫特征[3]，马尔可夫链广泛应用于自然科学和工程技术领域，对状态预测有较好的效果[4-6]。为解决混合动力汽车环境适应性的问题，本文中基于马尔可夫链思想，采用具有实际序列性的马尔可夫链混合动力汽车未来行驶状态预测模型，辨识和预测混合动力汽车未来运行状态，然后根据预测结果，进行更加合理高效的混合动力汽车能量管理控制，适应多变的交通状况。

1 HEV行驶工况预测控制原理

马尔可夫链预测模型是一种随机预测过程，在基于历史数据的基础上，确定研究对象发展的转移概率，根据上一时刻研究对象的状态预测下一时刻状态的计算过程，研究对象的第t+1状态值仅仅与第t次的状态值有关，由其状态值和转移概率乘积决定[7]。马尔可夫链的运动变化分析，主要是研究链内有限马尔可夫过程的状态和相互关系，进而预测链的未来状况，并据此作出决策。

车辆在连续行驶中，行驶状态转移过程由马尔可夫链形式表达，如图1所示。

图1中箭头为车辆行驶方向，在实车试验中，仪器采集数据的时间间隔为1s(频率为1Hz时)，即采集的时间变量是一个离散连续时间序列，因此图中每一个虚线所划分的方格都是车辆在该时刻内离散化后的行驶状态。因此车辆行驶状态的变化过程可以表达为连续离散时间t={…,i-3,i-2,i-1,i,i+1,i+2,i+3,…}的一个序列x(t)={…,x(i-3),x(i-2),x(i-1),x(i),x(i+1),x(i+2),x(i+3),…}。

汽车实际运行过程中，行驶工况中各个特征参数都可以进行离散化处理，而且变化过程具有很强的随机性，并且具有无后效性，系统内部的转移概率只与当前状态x(i)有关，而与之前的状态无关，所以车辆行驶状态转移过程具有马尔可夫性，本文中将着重研究基于马尔可夫链的混合动力汽车行驶工况预测。

2 行驶工况特征参数预测模型的建立

2.1 行驶工况特征参数

行驶工况中特征参数的选取直接影响到模型的预测结果，本文中选用了12个特征参数进行汽车行驶工况预测的研究。这些参数主要分为两部分：标准参数和波动参数[8-9]，见表1。

表1 样本参数

本文中汽车行驶工况特征参数全集为x，用向量{x1,x2,…,x12}进行表示，x1,x2,…,x12分别为表1中12个汽车行驶工况特征参数。针对不同的汽车行驶工况特征参数建立对应的基于马尔可夫链的预测模型，并对其预测准确性进行探讨。

2.2 运行车速采集

研究共选取两种汽车交通流量具有代表性的测试路线：第1种测试路段选择通过繁华市区且交通流量大的主干道，第2种测试路段选择车流量大的快速路(环路或高架路)。具体选择以下两条路线：通过繁华市区且交通流量大的主干道——长安街(公主坟至八王坟)；车流量大的快速路(环路或高架路)——三环路。采集时间为每天上午8：30～11：30，下午13：00～16：00。

采集车速曲线时间跨度很长，为了提高行驶工况预测模型的实时性，将其划分为短时间的速度-时间曲线片段。考虑到汽车在行驶过程中车速是一个时变量，随时间的不断变化而变化，新的车速会不断生成，而旧的车速则逐渐失去作用。为了提高预测模型的实时性，采用滚动时间窗的方式对速度-时间曲线进行分割，并在此基础上计算汽车行驶工况的各个特征参数。

滚动时间窗示意图如图2所示，设定车速采样间隔为T，滚动时间窗长度，即分段时间长度为NT，预测视距，即每次滚动时间长度为LT。

汽车的行驶状态由前N组车速数据来表示，即汽车当前的运行状态信息是由时间长度为NT的速度小片段内的所有车速组成的。随着汽车的行驶，时间窗长度为NT的速度小片段向前滚动，不断有新的车速输入和输出。设每次预测视距为LT，为了保持NT时间长度不变，当有新LT时间长度的车速加入时，最早的LT时间长度车速相应的从NT区间移出。

由于汽车行驶工况特征参数具有不同的动态范围，本文中通过归一化(见式(1))来消除特征参数动态范围不同带来的计算偏差，使得特征向量内部各个分量在预测识别计算时具有相同的贡献。

(1)

2.3 行驶工况特征参数的状态划分

设定汽车不同的行驶工况特征参数xm在每个行驶阶段含有Sm1，Sm2，…，Smn个可能状态：

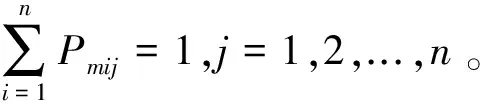
这里，不同行驶工况特征参数xm在汽车行驶过程中的行驶状态分别为：πm(1)=πm(0)Pmij，πm(2)=πm(1)Pmij，…，πm(i)=πm(i-1)Pmij，i=1，2，…，n。

(2) 假设汽车行驶工况特征参数在汽车行驶过程中的状态πm满足条件：πm=πmPmij，则该参数处于稳定状态。

2.4 状态转移概率矩阵计算

若状态集合S为n×n有限集合，则一阶齐次马尔可夫链的转移概率矩阵可表示为

(2)

一般的pmij满足以下条件：

(3)

从理论上讲，历史数据越长，状态划分越多，预测准确度越高，但状态划分过多，容易导致各状态样本点减少，转移概率规律性不强[10]。本文中将每个行驶工况特征参数平均划分为4个状态，即n=4。每个行驶工况特征参数xm看作是一个以{Sm1，Sm2，Sm3，Sm4}为状态空间的马尔可夫链。

表在主干道中的马尔可夫链的转移概率

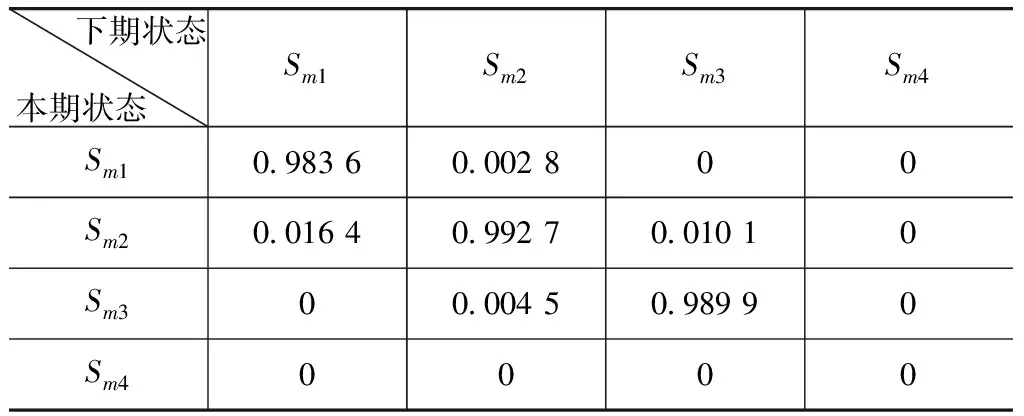
表3 σv在主干道中的马尔可夫链的转移概率

3 预测模型参数适值优化及准确度分析

在混合动力汽车行驶工况预测过程中，预测视距和滚动时域的大小直接影响预测和实时控制的准确度和效果，本文中对两者进行适值选取分析。其行驶工况预测准确度根据式(4)进行计算分析。

预测准确度Racc：

(4)

3.1 预测视距选取分析

应用上述基于模糊神经网络和马尔可夫链的车辆行驶工况特征参数预测模型，针对预测视距LT从1～30s逐次增加取值，图3为主干道和快速路两种路况下，预测准确度变化曲线。

由图可见，快速路工况预测准确度比较为拥堵的主干道行驶预测准确度高，但均随预测视距的逐渐增加，预测准确度逐渐下降，LT=1s时，快速路预测准确度为83.9%，当预测视距增加到30s时，预测准确度下降至70.3%。导致准确度下降的主要原因在于预测视距长度增加，新近状态转移信息无法加入，为保证预测的准确度，LT取1s。

3.2 滚动时间窗适值选取分析

混合动力车辆行驶特征参数从滚动时间窗中提取，如果时域过小，无法涵盖足够信息，如果过大，将包含了失去时效的信息。分别对滚动时间窗从160～220s进行了预测准确度分析，其准确度变化如图4所示。

随着滚动时域长度的变化，预测准确度没有明显的下降或改善，但滚动时间增加，计算速度有一定降低，此外，快速路工况预测准确度在滚动时间窗长度增加后有所降低，相反较为拥堵的主干道行驶预测准确度有所提高。

综合考虑预测模型的准确性和实时性，选用车速采样间隔为T=1s，预测视距为LT=1s，滚动时间窗长度为NT=180s。此时在繁华市区特征参数的预测准确度为90.1%，快速路预测准确度为70.5%。

4 预测结果分析

基于上述一阶齐次马尔可夫链行驶工况预测模型，对混合动力汽车整车能量管理进行了控制效果分析。

整车能量管理控制模型采用模糊神经网络控制策略[11](该部分在本文中不做重点介绍)。在运行过程中根据汽车运行状态预测模型的计算结果，在控制策略库中选择相应的最优模糊控制策略进行整车能量管理控制。

为验证预测效果，本文中另采用某市综合运行工况进行了预测仿真，运行工况由主干道和快速路两种运行工况组成，如图5所示。图6为运行工况预测识别结果。由图可见，在主干道运行工况中预测准确率略高，快速路部分路段车速特征介于主干道与快速路之间，预测状态产生频繁跳动，后续研究可通过细化运行状态类型和改进预测算法加以完善。图7和图8分别对比了有无工况预测时发动机转矩和电池SOC的时间历程。由图可见，在主干道行驶过程中，基于工况预测控制策略的发动机输出转矩低于无工况预测控制策略的发动机转矩，充分利用电机驱动，耗电量较大，电池SOC增长较慢；在快速路行驶过程中，基于工况预测的整车动力系统更多工作于发动机驱动和发电模式，发动机输出转矩增长至480N·m，电池SOC下降较慢，满足电机助力需求。在全程运行中，电池SOC波动较小，在满足动力性需求的同时，延长了电池使用寿命。

采用行驶工况预测与无行驶工况预测识别的整车控制方法相比，整车燃油经济性可提高3%左右，对进一步改善HEV的燃油经济性和排放性具有一定的促进作用。

5 结论

研究了混合动力汽车行驶工况预测的方法，建立了一阶齐次马尔可夫链行驶工况预测模型，对行驶工况特征参数进行了预测，并对预测中预测视距和滚动时间窗的适值选取进行了分析，与传统基于既定循环工况设计出的整车能量管理控制策略相比，基于工况预测的能量管理策略具有更好的燃油经济性。为新能源汽车能量管理实时控制提供了一种新方法。

但预测识别准确率在个别段较低，影响其燃油经济性的提升，主要是由于工况训练统计数据量有限和一阶马尔可夫链方法的限制，此外在实际运行中也会增加随机干扰等因素，在后续工作中将对算法进行进一步完善。

[1] Gong Q, Tulpule P. The Role of ITS in PHEV Performance Improvement[C]. 2011 American Control Conference (ACC 2011),San Francisco, CA, USA,2011:2119-2124.

[2] 舒红,高银平.中度混合动力汽车燃油经济性预测控制研究[J].公路交通科技,2009,26(1):149-153.

[3] Wang X, McGee R, Gillespie R B. An Energy Management Controller to Optimally Trade off Fuel Economy and Drivability for Hybrid Vehicles[J]. IEEE Transactions on Control Systems Technology: A Publication of the IEEE Control Systems Society, 2012, 20(6): 1490-1505.

[4] Crisostomi E, Schlote A. Traffic Modelling Framework for Electric Vehicles[J]. International Journal of Control,2012,85(7):880-897.

[5] 彭曲,丁治明.基于马尔可夫链的轨迹预测[J].计算机科学,2010,37(8):189-193.

[6] 邓鑫洋,邓勇.一种信度马尔科夫模型及应用[J].自动化学报,2012,4:666-672.

[7] Arrospide J, Salgado L. On-road Visual Vehicle Tracking Using Markov Chain Monte Carlo Particle Filtering with Metropolis Sampling[J]. International Journal of Automotive Technology,2012,13(6):955-961.

[8] 田毅,张欣,张昕,等.汽车运行状态识别方法研究(一)——特征参数选择[J].中国机械工程,2013,24(9):1258-1263.

[9] 田毅,张欣,张昕,等.汽车运行状态识别方法研究(二)——基于模糊神经网络的识别方法[J].中国机械工程,2013,24(11):1521-1530.

[10] 胡迪鹤.关于随机环境中的马尔可夫过程的简介[J].数学物理学报,2010,30A(5):1210-1241.

[11] 田毅,张欣,张昕.计及行驶工况影响的混合动力汽车控制策略[J].汽车工程,2010,32(8):559-663.