基于遗传算法的液力变矩器与发动机匹配的多目标优化

陈 凯，吴光强,2

(1.同济大学汽车学院,上海 201804； 2.东京大学生产技术研究所,东京 153-8505,日本)

前言

液力变矩器与发动机的合理匹配对提高车辆的动力性和经济性有着重要的影响。其匹配结果须针对不同车型的性能指标进行优化，以获得理想的共同工作点。随着计算机技术的发展，利用软件编程进行匹配分析和优化[1]，缩短了计算时间，提高了精度，已成为液力传动匹配优化中重要的手段。

文献[2]中对无级变速车辆提出从起步性能、燃油经济性等方面进行优化匹配，但优化中的设计变量，仅考虑了循环圆直径，这样得到的结果对于变矩器几何尺寸改动较大，不利于传动系的布置；文献[3]中通过分析变矩器结构参数对性能的影响，建立数据库，并以此建立优化模型，通过修改变矩器结构参数进行优化，但此优化方法依赖于数据库的精度与规模，并不通用。

事实上，匹配优化不仅与变矩器循环圆直径有关，还与各工况的泵轮转矩系数相关。通过已知的变矩器结构参数，根据一维束流理论和能量方程，可求出各工况下的循环流量系数，从而得到泵轮转矩系数[4]。据此，本文中建立了以泵轮出口角和导轮进出口角为设计变量的多目标优化模型，使用遗传算法进行液力变矩器与发动机的匹配优化，以提高两者匹配的动力性和经济性。

1 液力变矩器与发动机匹配计算方法

1.1 液力变矩器原始特性

液力变矩器的原始特性是反映变矩系数K、泵轮转矩系数λB和效率η随速比i变化的规律。表1为某款液力变矩器的主要性能参数。

表1 液力变矩器主要性能参数

1.2 发动机外特性

发动机的外特性主要指的是发动机的转矩Te、功率Ne和燃油消耗率be随发动机转速ne和油门开度α变化的关系。通过试验数据进行最小二乘法或者三次样条拟合得到发动机外特性曲线[5]。表2为某车型发动机主要参数，其稳态工况下输出转矩特性如图1所示。

表2 发动机主要参数

1.3 液力变矩器与发动机的共同工作特性

发动机与液力变矩器相结合时，仍按自身特性工作。当两者的转速和转矩相同时，才能够稳定地共同工作。

(1)

式中：TB为泵轮转矩，N·m；g为重力加速度，m/s2；λB为泵轮转矩系数，min2/(r2·m)；ne为发动机转速，r/min；nB为泵轮转速，r/min。

式(1)为发动机转矩Te和泵轮转矩TB的表达式。当液力变矩器与发动机处于稳定的共同工作状态时，两者的转速和转矩相同，即ne=nB，Te=TB。将式(1)中发动机转矩与泵轮转矩方程代入便可求得两者的共同工作点。在获得了共同工作输入特性后，通过不同工况下的共同工作点和液力变矩器的原始特性，计算得到涡轮轴转速nT、转矩TT和功率NT：

(2)

通过式(2)计算得到各转速比i所对应的涡轮轴转速、转矩和功率，经拟合后即可得液力变矩器与发动机共同工作的输出特性。

2 液力变矩器与发动机匹配优化设计

2.1 液力变矩器与发动机的匹配要求

对于液力变矩器与发动机的匹配，根据用途的不同，其评价指标和计算方法也有所不同。一般来说，合理的匹配应满足以下要求[6]：

(1) 起动工况，变矩器在i=0时的负载抛物线应在发动机最大转矩点附近，以使车辆在起步时能获得最大转矩；

(2) 液力变矩器在最高效率工况i=iη的负载抛物线应通过发动机最大功率所对应的转矩点，以使输出的功率最大；

(3) 液力变矩器与发动机的共同工作范围应处

于发动机燃油消耗率较低的区域，以提高车辆的燃油经济性。

2.2 液力变矩器与发动机匹配优化模型

根据一维束流理论和能量守恒定律建立能量平衡方程[7]，通过已知的液力变矩器基本参数可求得各工况下的无因次循环流量系数q，再根据转矩方程求得各流量下的叶轮转矩值，最后得到液力特性关系式：泵轮转矩系数λyB、变矩比Ky和泵轮液力转矩TyB的关系式分别为

λyB=(1+A1q)q

(3)

(4)

(5)

其中q为无因次循环流量系数：

q=Q/(ωBR3)

(6)

A1为泵轮和导轮联合工作时，中间流线的综合几何参数：

(7)

A2为泵轮和涡轮联合工作时，中间流线的综合几何参数：

(8)

rij,(i=B，T，D；j=1，2)表示各工作轮进出口的无因次半径(B、T、D分别表示泵轮、涡轮、导轮；j=1表示进口，j=2表示出口)：

rij=Rij/R

(9)

fij,(i=B，T，D；j=1,2)表示各工作轮进出口处的无因次流道面积：

fij=Fij/R2

(10)

式(3)～式(10)中：βij,(i=B，T，D；j=1,2)表示各工作轮进出口角；Rij，(i=B,T,D;j=1,2)表示各工作轮进口半径；Fij,(i=B,T,D;j=1,2)表示各工作轮进出口处的流道面积；R为变矩器特性半径，m；ωB为泵轮角速度，rad/s；λyB表示泵轮转矩系数，1/rad2；TyB表示泵轮液力转矩，N·m。

根据一维束流理论，对液力变矩器叶片进行形状设计，由于涡轮叶片铸造工艺复杂、要求高，因此以泵轮出口角和导轮的进出口角为设计变量，即X=(X1,X2,X3)=(βB2,βD1,βD2)，结合匹配要求，以两者匹配的动力性和经济性为目标函数，建立多目标优化模型：

minF(X)={F1(X),F2(X),F3(X)}

s.tGj(X)≥0 (j=1，2，3)

XL≤X≤XU

(11)

优化模型中，目标函数F1(X)表示失速时共同工作点应交于最高转矩点(4 000,238)附近：

(12)

F2(X)表示最高效率时共同工作点应交于发动机最高功率所对应的转矩点(6 500,200)附近：

(13)

F3(X)表示最高效率时共同工作点应交于发动机比燃油消耗较低区域的右边界所对应的转矩点(4 620,228)的左边：

(14)

约束条件G1(X)表示失速工况下的循环流量系数大于最高效率下循环流量系数：

G1(X)=q0-q0.9≥0

(15)

G2(X)对起动工况变矩比K0约束：

(16)

G3(X)对最高工况效率进行约束：

(17)

X的上下限分别设为

XU=[45,60,35]，XL=[35,50,25]

2.3 优化算法

对于多目标优化问题，使用Pareto遗传算法获得其全局最优解集。遗传算法[8]不对所求解问题的实际决策变量直接进行操作，而是通过构造非支配解集(non-dominated solutions)，对可行解集施加选择、交叉、变异、小生境、解集过滤等操作，慢慢逼近最优解集。对于上述优化模型，3个目标的最优边界构成一个曲面，边界上的任意一点都是最优解。

2.4 优化模型求解

优化模型的各控制参数设置为：群体规模M=800，交叉概率pc=0.6，变异概率pm=0.2，终止代数T=600。通过优化计算，得到Pareto最优解集，如图2所示。图中*号标注为目标函数优化前原始点值，即[βB2*,βD1*,βD2*]=[41.75,56.19,29.52]，不在Pareto最优边界上。

3 液力变矩器与发动机匹配结果评价

3.1 液力变矩器与发动机匹配评价

液力变矩器与发动机共同工作的性能优劣直接影响整车的动力性和经济性，须做量化的评价，常用的指标分为非积分指标和积分指标，包括最大输出转矩MTmax、起步时变矩器转矩容量MP1000、高效转速范围dm、高效工作范围内平均输出功率PTj2、高效工作范围内平均燃油消耗率bej2和动力经济性综合指标E(=PTj2/bej2)。

3.2 匹配优化模型评价

选取Pareto最优曲面上一点[βB2,βD1,βD2]=[37.36,57.04,28.55]与优化前进行对比，优化前后液力变矩器结构参数如表3所示。

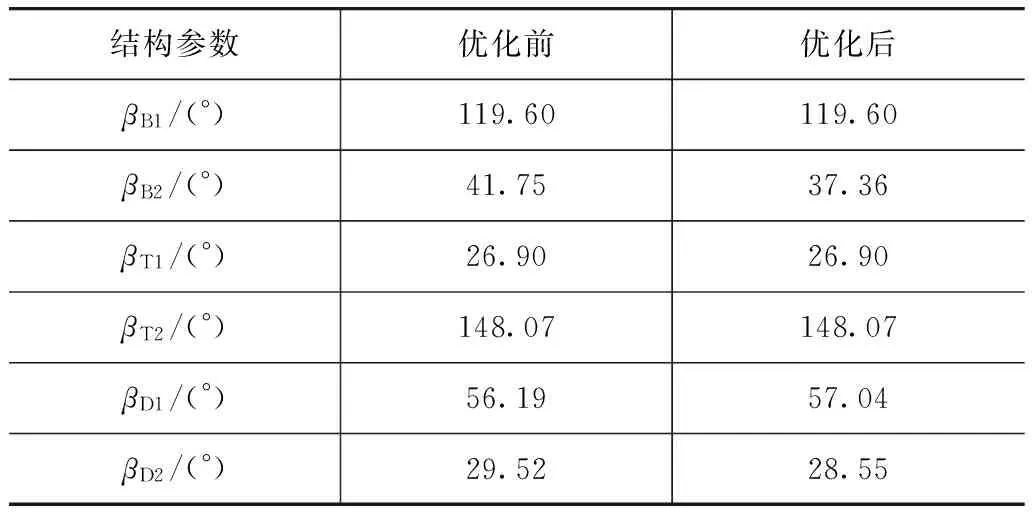
表3 优化前后液力变矩器结构参数对比

图3为液力变矩器原始特性在优化前后的对比，可以发现，在效率小幅提高的情况下，各速比工况下的变矩比增大，泵轮转矩系数λB减小。

分别将发动机的40%、60%和100%油门开度下的净转矩曲线，及优化前后液力变矩器的各工况泵轮负载抛物线绘制在同一个坐标系内，得到两者共同工作的输入特性，如图4所示。由图可见，优化后，由于泵轮转矩系数的减小，使得液力变矩器负载曲线与发动机特性曲线的交点向右偏移，各工况下所得的共同工作点所对应的转矩皆增大，提高了整车的加速性能。并且，优化后泵轮负载曲线仍穿过燃油消耗低的区域。

在获得了两者共同工作的输入特性后，通过式(2)拟合得出共同工作的输出特性。图5为优化前后100%油门开度下发动机与液力变矩器的输出特性曲线，优化后涡轮输出转矩、输出功率和效率皆提升，并且涡轮转速范围增大。

表4为评价液力变矩器与发动机匹配结果的主要指标。可以看出：优化后，失速工况下涡轮最大输出转矩MTmax增加7.2%，提高了车辆的起步性能与爬坡性能；起步时变矩器转矩容量MP1000减小15.9%，这使起步时发动机转速提升更快，从而使变矩器与发动机更快地达到共同工作转速，提高了起步加速性能。在变矩器高效转速范围内，涡轮输出的功率PTj2较优化前增加10.73%，说明变矩器更大程度地传递了发动机的功率；同时，优化后高效转速范围内的燃油消耗率bej2稍有降低，提升了燃油经济性；而工程上注重的动力性综合指标E提高了11.9%，整车的综合性能更加优越。通过多目标优化，改善了液力变矩器与发动机的匹配性能，提高了整车的动力性和经济性。

表4 优化前后匹配评价指标对比

4 结论

(1) 介绍了液力变矩器与发动机的匹配方法，对发动机模型与液力变矩器模型进行了匹配计算，得到两者共同工作的输入输出特性。

(2) 根据一维束流理论和能量方程，以动力性和经济性为匹配要求，建立以泵轮出口角和导轮进出口角为设计变量的多目标优化模型，通过遗传算法计算得到了Pareto最优解集。

(3) 选取Pareto最优边界上一点，计算得到优化后液力变矩器的结构参数；依据各匹配评价指标，通过优化前后的对比发现，优化后液力变矩器与发动机匹配动力性提升明显，高效工况的经济性略有提高，证明了优化模型的正确性。

参考文献

[1] 孙跃东,周萍,邹敏,等.发动机与液力变矩器匹配的计算机软件开发[J].汽车工程,2004,26(6):702-704.

[2] 刘振军,秦大同,胡建军.无级变速车辆发动机与变矩器共同工作特性[J].重庆大学学报(自然科学版),2002,25(12):14-17.

[3] 桂勇,骆清国,孔令伟,等.基于液力变矩器与发动机匹配工作性能的液力变矩器结构参数优化[J].装甲兵工程学院学报,2009,23(1):45-49.

[4] 陈曙光,吴光强,王欢.液力变矩器叶栅参数的优化研究[J].工程机械,2008,39(8):50-54.

[5] 李金辉,徐立友.基于MATLAB语言的发动机特性研究[J].汽车科技,2005(3):40-42.

[6] 朱经昌.液力变矩器的设计与计算[M].北京:国防工业出版社,1991,10:13-32,68-72.

[7] Dong Yu, Vamshi Korivi, Pradeep Attibele, et al. Torque Converter CFD Engineering Part I: Torque Ratio and K Factor Improvement Through Stator Modifications[C]. SAE Paper 2002-01-0884.

[8] Kikuo Fujita, Noriyasu Hirokawa, Shinsuke Akagi, et al. Multi-objective Optimal Design of Automotive Engine Using Genetic Algorithm[C]. ASME Design Engineering Technical Conferences,1998.