THE CORRESPONDENCE THEOREM FOR COALGEBRAS

ZHU Jia-gui

（Departmentof Mathematics,Chaohu College,Chaohu Anhui 238000）

1 Introduction

On the fundamental homomorphism theo-rem for coalgebras,the existing monographson the subject,such as the books of[1]，[2]or[3],have given statement and proof.For example,the fundamental homomorphism theorem for coalgebras in[3]was stated as following：

TheoremSuppose that C is a coalgebraover the eld k.

（1）Let I be a coideal of C.Then the quotient space C/I has a unique coalgebra structure so that the linear projection π:C → C/I is a coalgebra map.

Suppose D is also a coalgebra over k and that f:C→D is a coalgebra map.Then

（2） Kerf is a coideal of C,and if I is a coideal of C such that I⊆Kerf then there is a unique coalgebra map f:C/I→ D such thaπ =.

（3） Suppose that f is onto and let I=Kerf.Then there is a unique isomorphism:C/I→D of coalgebras such thatπ=f.

As compared with the usual algebraic systems like group,ring,module and Lie algebra,under surjective homomorphism map,the correspondence relation of subobjects for coalgebras has not been given in any literature.Without loss the generality,we observe the subgroups of a quotient group.The following description is given in[4].

TheoremLet G be a group,N◁G a normal subgroup,and let π :G → G/N be the natural map.Then

is a bijection from{H＜G,H⊇N},the family of all those subgroups H of G that contain N,and{K＜G/N},the family of all the sub groups of G/N.

Moreover,under this correspondence,normal subgroups of G correspond to normal subgroups of G/N.

If H◁G,N⊆H,then G/H≌G/N/H/N,i.e.,G/H ≌ G/N/π（H）.

If we substitute ring,module,Lie algebra for group,subring,submodule,Lie subalgebra for subgroup respectively,similar results still hold.We will generalize this fact to coalgebra case.

2 Main Results

Throughout,we work over a field k.For basic denition and facts about coalgebras we refer to[2]and[3].In particular the comultiplication and counit of a coalgebra C is denoted by △Cand εCrespectively.Our main result is the following theorem.

Theorem 2.1 Let C be a coalgebra,I a coideal of C,let π :C → C/I be natural coalgebra map.Then

（1）π :J→ π（J）=J/I is a bijection from{J＜C,I⊆J},the family of all those subcoalgebras J of C that contain I,and{L＜C/I},the family of all the subcoal-gebras of C/I.

Moreover,under this correspondence,coideals of C correspond to coideals of C/I.

（2）If J◁ C is a coideal and J⊇ I,then C/J≌C/I/π（J）.

The proof of this theorem is based on the following lemmas.

Lemma 2.2 Suppose that f:C→D is a coalgebra map,we have

（1） If C1is a subcoalgebra of C,then f （C1）is a subcoalgebra of D;

（2） If I is a coideal of C,then f （I） is a coideal of D;

（3） If J is a coideal of D,then f-1（J）is a coideal of C.

Proof.（1）For any c∈C1,we have

△C（c）∈C1⊗ C1,because C1is a subcoalgebra of C.Thus

It follows that△D（ f（C1））⊆ f（C1）⊗ f（C1）.Hence f（C1） is a subcoalgebra of D.

（2）Since I is a coideal of C,we have

△C（I） ⊆ C ⊗ I+I⊗ C,and εC（I） =0.Then

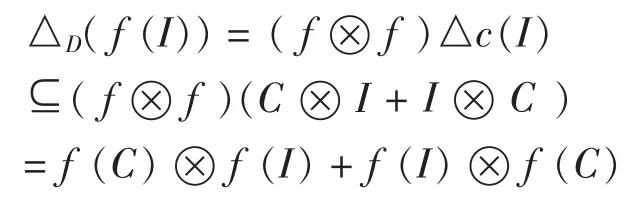
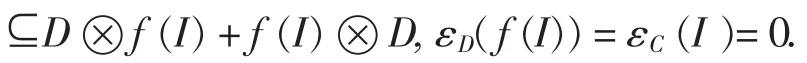
This implies that f（I） is a coideal of D.

（3）Let f-1（J）={c∈C,f（c）∈J}.It is suffcient to show that

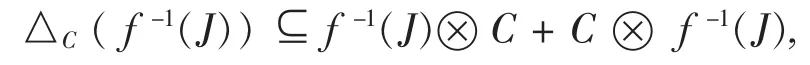
and

For any c∈（ f-1（J））,εC（c） = εD（ f（c））∈εD（J） =0,hence εC（f-1（J））=0.

We consider the projection π：D → D/J.

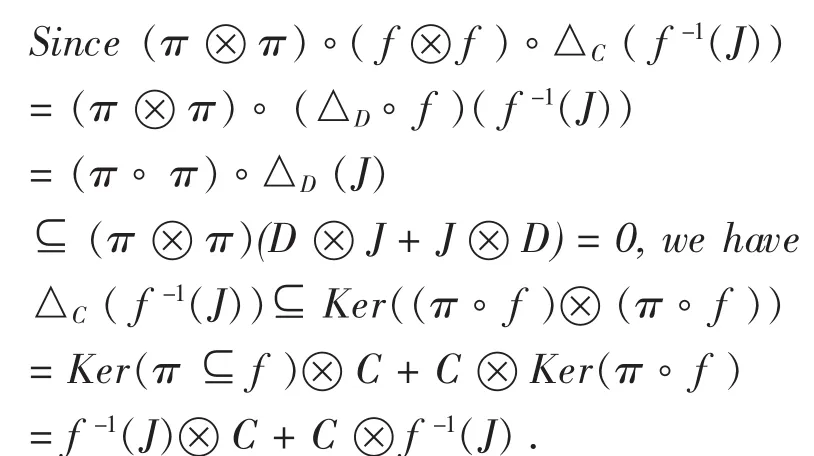
Lemma 2.3 （Characterization of subcoalgebras in a quotient coalgebra）

Let C be a coalgebra and I⊆C a coideal.Then L is a subcoalgebra of the factor coalgebra C/I if and only if L=J/I for some subcoalgebra J of C such that I⊆J.

ProofLet π :C → C/I be the natural projection.Then π-1（L）={c∈C, π（c）∈L}.We need show that π-1（L） ⊇ I and

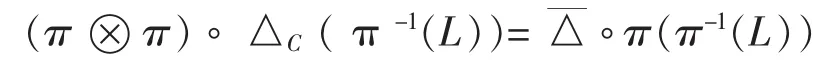
It follows that△C（π-1（L））⊆ π-1（L）⊗π-1（L）.

Set π-1（L）=J,then L= π（J）=J/I.

We are now in a position to give the proof of the main result.

Proof of Theorem 2.1.（1） By lemma 2.3,if J is a subcoalgebra of C and I⊆ J,then π（J）=J/I is a subcoalgebra of C/I.Conversely,if L is a subcoalgebra of C/I,then π-1（L）={c∈C,π（c）=c+I∈L}is a subcoalgebra of C,π（L） ⊇ I and π（π-1（L））=L.

According to the defnition of π-1, we know that π-1（π （J））⊇ J for any subcoalgebra J of C.We show that π-1（π（J）） =J when J ⊇ I.

Let c∈π-1（π（J））,then π（c）∈π（J）,and so there exists some element j∈J such that π（c）= π（j）.This imply π（c-j）=,i.e.c-j∈I,or c∈ j+I⊆ J.Thus π-1（π（J）） =J.

We have showed all those subcoalgebra of C that contain I are one to one correspondence to all subcoalgebras of C/I.By lemma 2.2 （2） and （3）,we know that,under this correspondence,coideals of C correspondence tocoideals of C/I.That is,π is also a bijection from the family of all those coideals of C that contain I and the family of all the coideals of C/I.

（2） Since π（J） is a coideal of C/I,C/I/π（J）is a quotient coalgebra.

Let φ ：C/I→ C/I/π（J） is the natural coalgebra map,then φπ ：C → C/I/π（J）is a coalgebra map.Since Kerφ = π（J）,we have Ker（φπ）= π-1（π （J））=J.By the fundamental homomorphism Theorem,we obtain C/J ≌ C/I/π（J）.Because π（J）=J/I,we have C/J≌ C/I/J/I.

Up to now,we give,under surjective homomorphism, the correspondence relation of subobjects between coalgebras.It is worth pointing out that,under general homomorphism,preimage of subobject is still subobject for group,ring,module or Lie algebra.But this result is not hold for coalgebra.In the other word,the preimage of a subcoalgebra need not to be a subcoalgebra for general coalgebra homomorphism.

Example.Set C=k+kx=k[x]/ （x2）,D=k.C and D has a natural coalgebra structrue.

For example,in C,△（1） =1 ⊗1,△（x） =1⊗x+x⊗1.

Consider the coalgebra map f:C→D which sends 1 to 1 and x to 0.Then it is easy to show that the preimage of the 0 subcoalgebra of D is not a subcoalgebra of C.In fact f-1（0） =kx which is not closed under coproduct.

This is just equivalent to say that for a morphism of algebras, the image of an ideal may not be an ideal.

[1] Montgomery,S.,Hopf algebras and their actions on rings,CBMS Reg.Conf Series 82,Providence,R.I.,1993.

[2] Daˇscaˇlescu,S.,Naˇstaˇsescu,C.,Raianu,S.,Hopf Algebras.An Introduction,Marcel Dekker,New York-Basel,2001.

[3] Lambe,L.A.,Radford,D.E.,Introduction to the Quantum Yang-Baxter Equation and Quantum Groups：An Algebraic Approach,Kluwer Academic Publishers,1997.

[4] Jacobson,N.,Basic Algebra I,W.H.Freeman and Company,1974.