基于Matlab压电超声换能器匹配电路的研究
2014-02-24张伟涛张永俊
张伟涛,张永俊,姚 震
(广东工业大学机电工程学院,广东广州510006)
基于Matlab压电超声换能器匹配电路的研究
张伟涛,张永俊,姚 震
(广东工业大学机电工程学院,广东广州510006)
为了使超声振子获得良好的振动效果,必须设计高效的匹配电路。对单个电感、电容的串联和并联匹配电路进行了研究。利用等效电路法推导出匹配电路的阻抗公式,根据该公式,采用Matlab平台仿真得到不同参数的各匹配电路阻抗特性曲线。通过分析阻抗特性曲线得出匹配电路及匹配参数对系统谐振频率、阻抗及机电耦合系数的影响规律。实验结果表明:仿真结果与实验结果一致,所得结论为压电换能器匹配电路的设计提供了理论依据。
匹配电路;压电换能器;谐振频率;阻抗;机电耦合系数
随着超声技术的不断研究与发展,超声加工、超声焊接及超声清洗等大功率超声技术的应用越来越广泛。超声应用的核心设备主要由超声波电源、匹配电路及换能器等构成。其中,匹配电路能较好地实现系统能量高效传输,有效降低各部分之间多次反射造成的能量损失,保证超声系统安全高效的运行。目前,匹配电路已成为超声技术应用领域中的研究热点之一。
匹配电路一般采用电感或电容等储能型元件构成,以减少其自身的损耗。换能器的本质属于一种谐振系统,由于加入了匹配电路中的电感和电容,使换能器的性能受到一定程度的影响。文献[1]在忽略动态电阻的情况下,推导出单个电感、电容串联和并联匹配的电抗或电纳特性曲线,从中得到电感、电容的加入会对谐振频率和机电耦合系数产生不同的影响,但未充分论证电感、电容的加入会对系统阻抗产生何种影响。文献[2-6]研究了电感、电容组合匹配电路,推导了匹配电路在谐振频率处的阻抗公式及最佳匹配元件的参数。然而,匹配元件的加入会使谐振频率发生改变,导致计算结果与实际情况存在一定的误差。由于实际工程应用对匹配电路性能的要求越来越高,因此,对匹配电路进
行研究是极有必要的。
针对上述问题,本文对压电换能器的单个电感、电容的串联和并联匹配电路进行了研究。根据推导得出的各匹配电路全频域的等效阻抗计算公式,采用Matlab平台绘制不同大小匹配元件、匹配换能器系统的阻抗特性曲线,通过分析阻抗特性曲线得到匹配元件对系统匹配后的阻抗、谐振频率及机电耦合系数的影响。
1 换能器等效电路
压电换能器在基频附近的等效电路模型见图1a。其中,C0为静态电容,L1、C1、R1分别为动态电感、动态电容、动态电阻,三者组成的支路称为动态支路[6]。根据图1a可得压电换能器等效阻抗为Zd:

其中,

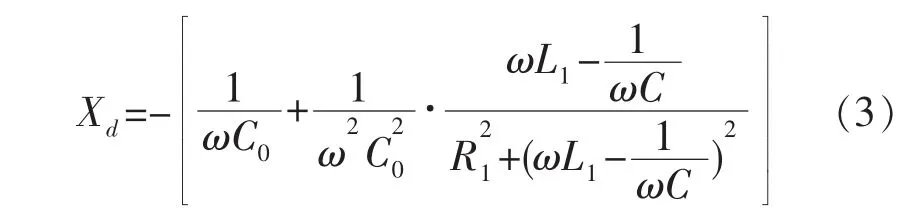
式中:C=C0C1/(C0+C1);ω=2πf。
根据式(1)可将图1a转化为图1b。其中,Rd和Xd分别表示换能器的等效电阻和等效电抗。
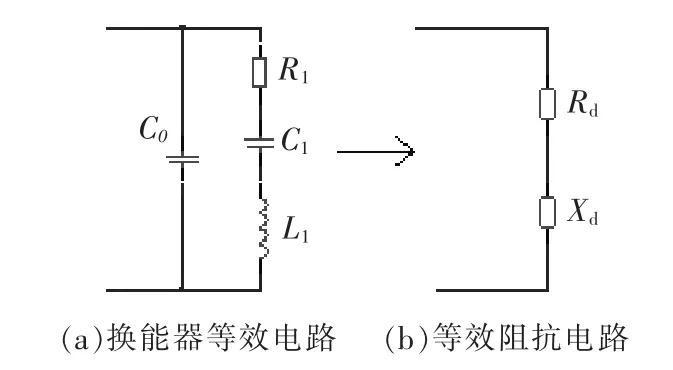
图1 压电换能器等效电路
2 匹配电路仿真
换能器匹配电路的拓扑结构有多种,但基本上是由单个电感或电容组合而成的感性网络。本文主要研究单个电感的串、并联和单个电容的串、并联匹配电路特性,其拓扑结构见图2。
为便于研究,选取一个换能器,其参数见表1。将各参数代入式(1)可得无匹配时的换能器阻抗特性曲线。图3~图6所示的L=0 mH、C=0 nF分别表示所对应的无匹配时的换能器阻抗特性曲线。
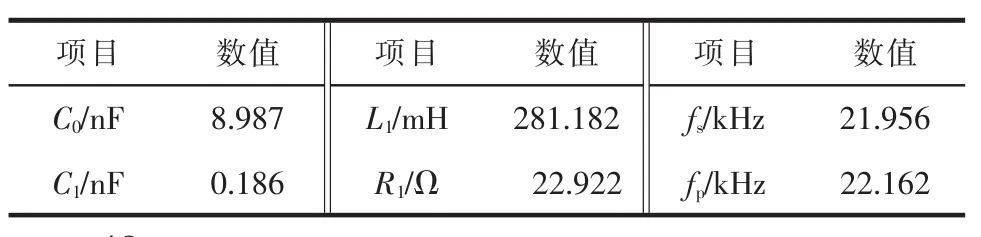
表1 换能器初始参数
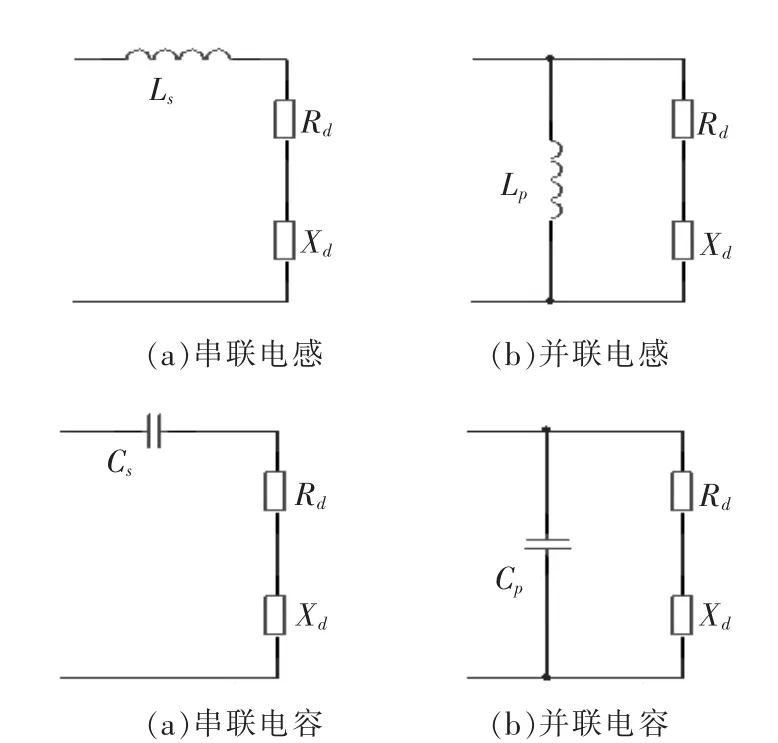
图2 各匹配电路的拓扑结构
2.1 串联电感匹配
串联电感匹配的拓扑结构见图2a,由此可推出其等效阻抗公式:
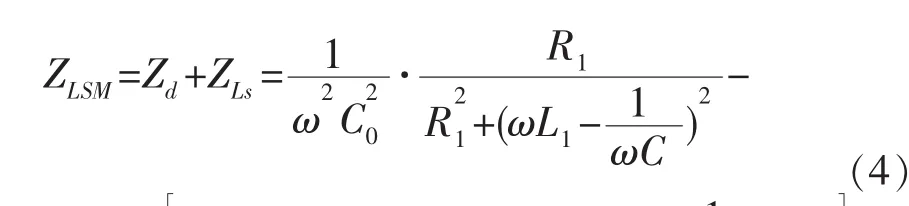
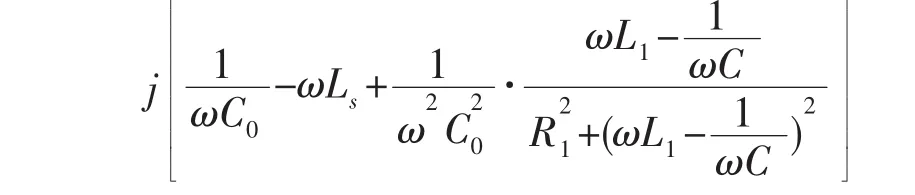
将表1所示的参数分别代入式(1)和式(4),匹配电感Ls取值为1.5、2.1 mH。采用Matlab平台,仿真得到无匹配时的换能器阻抗特性曲线和匹配后系统的换能器阻抗特性曲线(图3)。
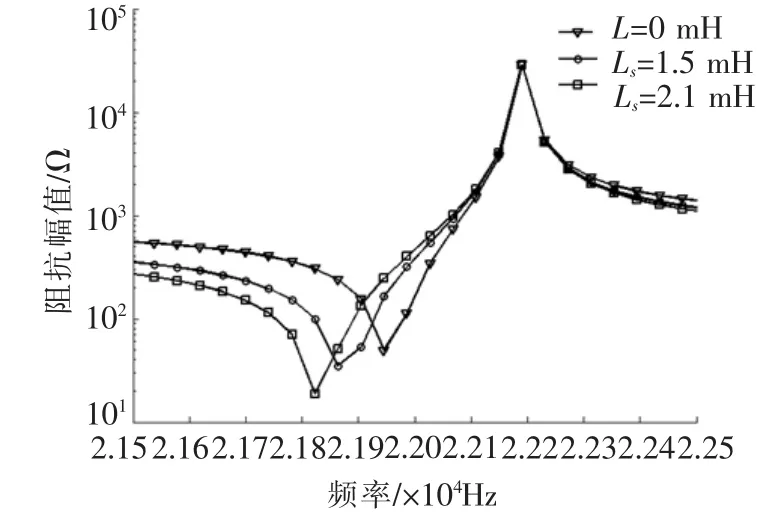
图3 串联电感阻抗特性曲线
由导纳理论可知,阻抗最小时对应频率为串联谐振频率fs;阻抗最大时对应频率为并联谐振频率fp[4]。图3所示的3条曲线的阻抗最大值Zmax相同,说明串联电感匹配对匹配后系统的最大阻抗值Zmax无影响,即表明串联电感匹配不会影响系统的并联谐振频率fp。从图3还可看出,3条曲线的阻抗最小值Zmin各不相同,串联电感的加入使匹配后系统的最小阻抗Zmin变小;且当串入的电感Ls越大时,新的Zmin越小。这表明串联电感匹配会对系统串联谐振
频率fs产生影响,匹配后系统串联谐振频率fs会变小,且匹配电感Ls越大,新的串联谐振频率fs越小。根据机电耦合系数的公式:
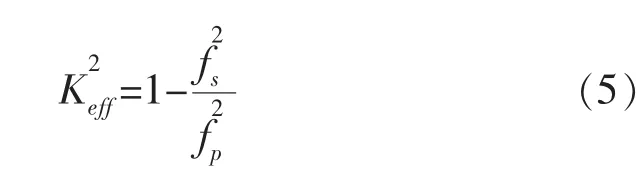
可知,当fs减小、fp不变,则机电耦合系数Keff逐渐增大。因此,串联电感匹配后,系统Keff是一个增函数,且当Ls越大时,新的Keff越大。
2.2 并联电感匹配
并联电感匹配的拓扑结构见图2b,由此可推出匹配后的系统阻抗表达式:
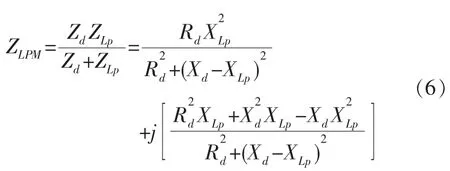
式中:ZLp=jXLp=jωLp为并联电感Lp的阻抗;ZLPM表示并联电感匹配后的系统阻抗。
将表1所示的参数分别代入式(6),匹配电感Lp取值为10、12 mH。采用Matlab平台,仿真得到无匹配时的换能器阻抗特性曲线和匹配后系统的换能器阻抗特性曲线(图4)。
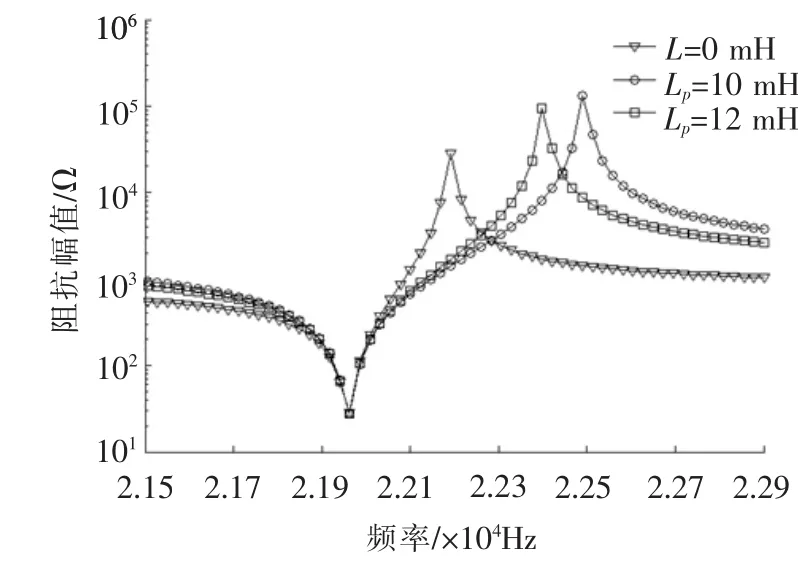
图4 并联电感阻抗特性曲线
从图4可看出,3条曲线的阻抗最小值重合,即串联谐振频率点重合,说明并联电感的加入对系统的串联谐振频率fs没有影响。然而,每条曲线的阻抗最大值各不相同,即并联谐振频率点fp没有重合,说明并联电感Lp对系统的并联谐振频率fp有影响,使并联谐振频率fp升高,且并联电感Lp越小,并联谐振fp越大。并联电感Lp后,阻抗最大值比没有匹配时都有所增加,且电感Lp越小,新的阻抗最大值Zmax越大。这是因为并联电感匹配后,系统的串联谐振频率fs不变,并联谐振频率fp变大,根据式(5)可知,并联电感匹配后系统的机电耦合系数会变大,且并联的电感Lp越小,机电耦合系数越大。
2.3 串联电容匹配
串联电容匹配的拓扑结构见图2c,由此可推导出串联电容匹配后系统的阻抗表达式:
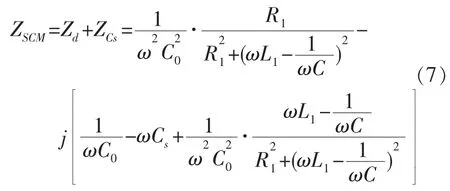
为串联电容Cs的阻抗;ZSCM表示串联电容匹配后的系统阻抗。
将表1所示的参数分别代入式(7),串联电容Cs取值为10、15 nF。采用Matlab平台,仿真得到无匹配时的换能器阻抗特性曲线和匹配后系统的换能器阻抗特性曲线(图5)。
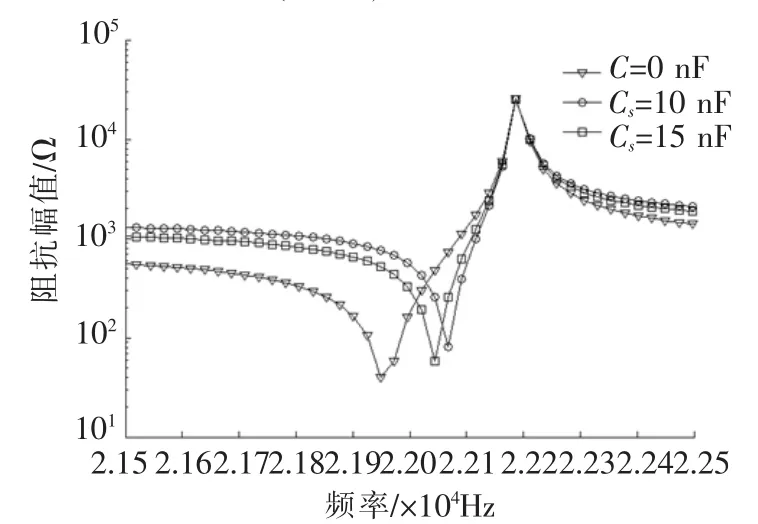
图5 串联电容阻抗特性曲线
由图5可知,不同匹配电容Cs对应的阻抗最大值Zmax几乎相同,即并联谐振频率点fp重合,说明匹配电容Cs对匹配后系统的并联谐振频率没有影响,对最大阻抗值Zmax也无影响。不同电容Cs匹配时的最小阻抗值Zmin差别较大,即串联谐振频率不同,表明电容Cs对串联谐振频率fs有影响。匹配后的串联谐振频率fs均大于无匹配时的串联谐振频率,且当匹配电容Cs越小时,新的串联谐振频率fs越大。匹配后的最小阻抗值Zmin比无匹配时的最小阻抗值要大,且匹配电容Cs越小,匹配后的最小阻抗值Zmin越大。由机电耦合系数公式(5)可知,由于串联电容匹配后,系统的fp不变,fs变大,所以经串联电容匹配后,系统的机电耦合系数Keff变小,且匹配的电容Cs越小,机电耦合系数Keff越小。
2.4 并联电容匹配
并联电容匹配的拓扑结构见图2d,由此可推导出并联电容匹配后系统的阻抗表达式:
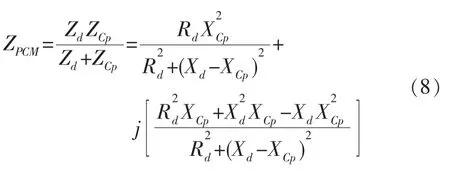
将表1所示的参数分别代入式(8),并联电容Cp取值为10、15 nF。采用Matlab平台,仿真得到无匹配时的换能器阻抗特性曲线和匹配后系统的换能器阻抗特性曲线(图6)。
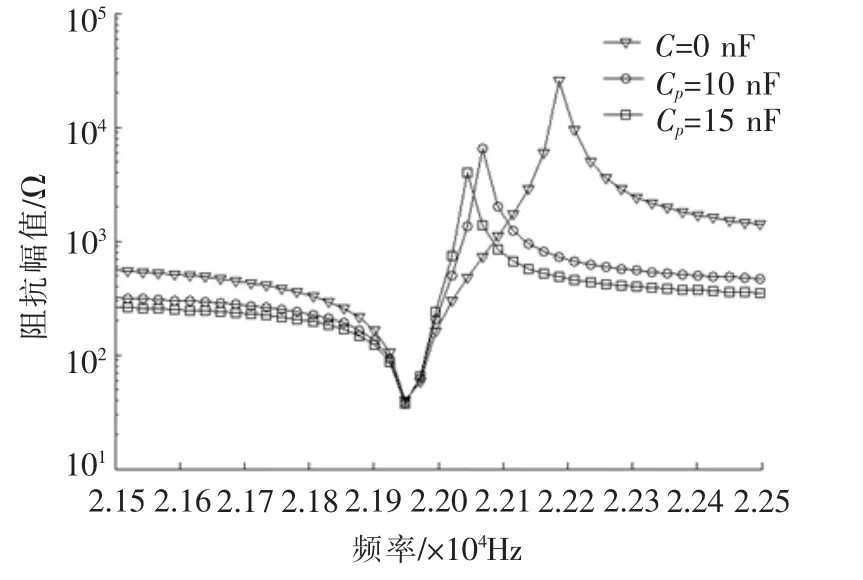
图6 并联电容阻抗特性?曲线
由图6可知,不同匹配电容Cp对应阻抗曲线的阻抗最小值Zmin相同,即串联谐振频率fs重合,表明并联电容匹配对系统的串联谐振频率fs没有影响。不同并联电容Cp所对应的阻抗最大值Zmax各不相同,即并联谐振频率点fp分布较分散,表明并联电容匹配对系统的并联谐振频率有较大影响。经电容Cp匹配后,新的并联谐振频率点fp都比无匹配时低,且Cp越大,新的fp越小。匹配后的阻抗最大值Zmax比无匹配时都小,且匹配电容Cp越大,新的阻抗最大值Zmax越小。由机电耦合系数公式(5)可知,由于并联电容匹配后,系统的fs不变,fp变小,所以经并联电容匹配后,系统的机电耦合系数Keff变小,且匹配电容Cp越大,机电耦合系数Keff越小。
3 实验结果与分析
为了验证上述仿真结果的正确性,本文进一步对各匹配电路进行对比实验。实验换能器与仿真换能器型号相同,参数同表1。实验检测平台为PV70A阻抗分析仪,测试结果见表2。
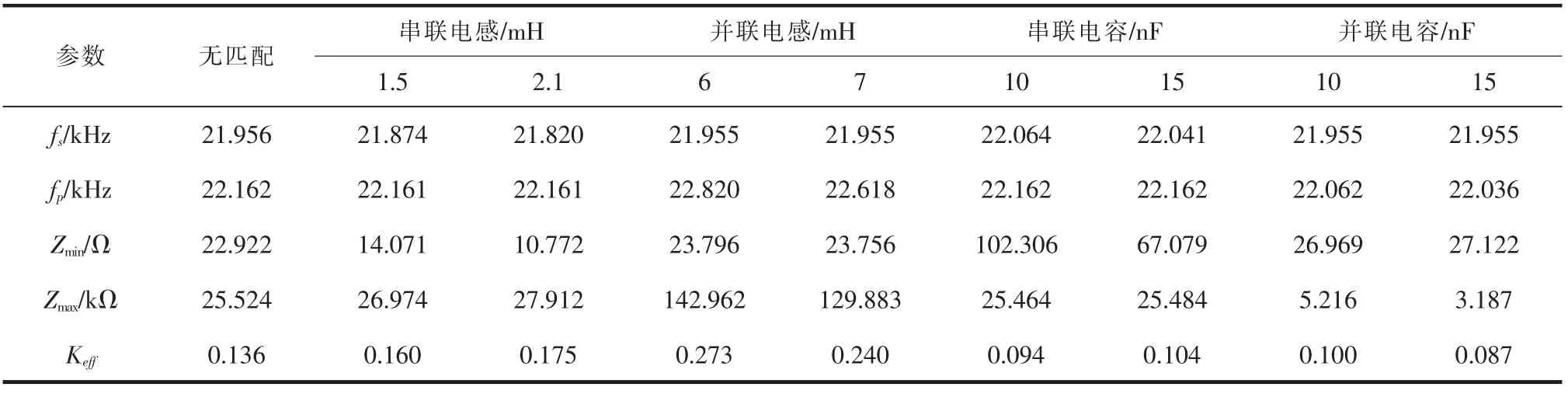
表2 匹配后的换能器测试参数
从表2可看出,实验结果与仿真结果呈现一致性。综合分析可知,各匹配电路具有如下特性:
(1)串联电感匹配使系统的串联谐振频率fs变小,串联电容匹配使系统的串联谐振频率fs变大,这两者对系统的并联谐振频率fp几乎没有影响;并联电感匹配使系统的并联谐振频率fp变大,并联电容匹配使系统的并联谐振频率fp变小,两者对串联谐振频率fs的影响可忽略。
(2)串联电感匹配使系统的最小阻抗值Zmin变小,串联电容匹配使系统的最小阻抗值Zmin变大,两者对系统最大阻抗值Zmax的影响可忽略;并联电感匹配使系统的最大阻抗值Zmax变大,并联电容匹配使系统的最大阻抗值Zmax变小,两者对系统最小阻抗值Zmin的影响可忽略。
(3)串联电感匹配和并联电感匹配都使系统的机电耦合系数Keff变大;串联电容匹配和并联电容匹配都使系统的机电耦合系数Keff变小。
4 结束语
本文对换能器匹配电路进行了深入研究,采用Matlab平台进行仿真,分析了单个电感、电容元件的串、并联匹配电路对换能器系统的影响。仿真结果与实验结果呈现一致性,所得结论为匹配电路设计提供了新的思路。
[1] 林书玉.匹配电路对压电陶瓷超声换能器振动性能的影响[J].压电与声光,1995(3):27-30.
[2] 林书玉,张福成.压电超声换能器的电端匹配电路及其分析[J].压电与声光,1992(4):29-32.
[3] 郭建中,林书玉,郭勇亮.压电换能器电端匹配电路的优化[J].测控技术,2004(8):73-75.
[4] 方由艳,高炳山.匹配网络对换能器谐振频率影响的研究[J].声学技术,2009,28(2):51-52.
[5] Garcia-Rodriguez M,Garica-Alvarez J,Yañez Y,et al. Low cost matching network for ultrasonic transducer[J]. Physics Procedia,2010,3(1):1025-1031.
[6] 郭林伟,林书玉,许龙.压电陶瓷换能器电感与电容匹配特性研究[J].陕西师范大学学报,2010(2):39-42.
Study of the Matching Circuits of Piezoelectric Ultrasonic Transducer Based on Matlab
Zhang Weitao,Zhang Yongjun,Yao Zhen
(Guangdong University of Technology,Guangzhou 510006,China)
In order to obtain good vibration performance of ultrasonic vibrator,the efficient matching circuit must be designed.The single inductance and capacitance of the series and parallel matching circuit is studied.Using the method of equivalent circuit,matching circuit impedance formula is derived.According to the impedance formula,the different parameters of the impedance matching circuit characteristic curve are obtained by Matlab simulation platform.Through analyzing the impedance characteristic curve,the influence laws of matching circuit and parameters on system resonance frequency,impedance matching and electromechanical coupling coefficient are found out. The experimental results show that the simulation results are consistent with the experimental results. The conclusion provides some theoretical basis for design of matching circuits of piezoelectric transducer.
matching circuit;piezoelectric transducer;resonant frequency;impedance;electromechanical coupling coefficient
TG663
A
1009-279X(2014)02-0047-04
2013-12-26
广东省科技厅粤港关键领域重点突破项目(2006A15101004)
张伟涛,男,1989年生,硕士研究生。
