对称反循环矩阵求逆的探讨
2014-02-24蒋加清
蒋加清
(台州学院 教师教育学院,浙江 临海 317000)
对称反循环矩阵求逆的探讨
蒋加清
(台州学院 教师教育学院,浙江 临海 317000)
根据对称反循环矩阵的性质,利用生成多项式和特征多项式,采用行初等变换的方法,给出了求对称反循环矩阵的逆的一种方法,有一定的实用性。
生成矩阵;对称反循环矩阵;次对角阵;生成多项式;可逆;初等行变换。
两类r—循环矩阵的研究为不少作者所关注[1-5],文献[4]研究了对称反循环矩阵的充要条件,但目前很少看到对称反循环矩阵求逆问题.受文[3]的启发,本文利用多项式矩阵的初等行变换给出了对称反循环矩阵的算法,该算法简便、实用.
1 定义与性质

g(x)关于矩阵N的生成矩阵B,称为反循环矩阵,
多项式为m(x)=xm+1,则m(N)=0,称m(x)为矩阵N的最小零化多项式.
其中矩阵M1称为m阶基本对称反循环矩阵,简记为.,
规定Mm=Rm.可以验证.
性质1[4]设矩阵A∈Cm×m,则矩阵A=SC-1(b0,b1,…,bm-1)的充要条件是.
性质2[3]设矩阵B=C-1(b0,b1,…,bm-1)可逆的充要条件是g(x)与m(x)互素.
性质3[2],
且Ni-1=M1Mi或Mi=M1Ni-1(i=1,2,…,n).
对称循环矩阵与对称反循环矩阵有以下矩阵关系.

2 主要结果
定理1若矩阵A是对称反循环矩阵,则矩阵A-1也是对称反循环矩阵.
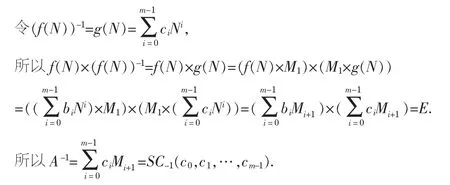
因此对称反循环矩阵的逆矩阵是对称反循环矩阵.
定理2矩阵A=SC-1(b0,b1,…,bm-1)可逆的充分必要条件是互素.
而M1可逆,所以A可逆的充分必要条件是f(N)可逆.而f(N)的生成多项式是,根据性质2,所以A可逆的充分必要条件是f(x)与m(x)互素.
定理3矩阵A=SC-1(b0,b1,…,bm-1)可逆,则,其中.
证明:因为A×M1=f(N),而f(N)的生成多项式是,根据定理2,所以A可逆的充分必要条件是f(x)与m(x)互素.从而存在多项式u(x)、v(x)∈P[x],使得f(x)u(x)+m(x)v(x)=1.取x=N,则有f(N)u(N)+m(N)v(N)=Em.又因为m(N)=0,所以f(N)u(N)=Em,即,其中.
根据定理3,求A-1=M1×u(N),只要求u(x),文献[6]用辗转相除法求u(x),计算量较大.本文通过多项式矩阵的初等行变换求u(x),方法简便.
推论1若矩阵A=SC-1(b0,b1,…,bm-1)可逆,其中,作多项式矩阵Q(x)=,对它进行一系列初等行变换化为,则SC-1(c0,c1,…,cm-1),其中.
得出对称反循环矩阵求逆算法步骤如下:
3 应用举例

因为d(x)=1,所以矩阵A可逆.
[1]沈光星.关于r—循环系统的计算复杂性[J].数学研究与评论,1992,12(4):595-598.
[2]董建新,周建军,曹永和.对称r—循环矩阵的结构及其特征值[J],华中师范大学学报(自然科学版),1997,31(2):129-132.
[3]蒋加清.r—循环矩阵求逆的一种新算法 [J].高等数学研究,2012,15(1):62-65.
[4]何承源.对称反循环矩阵的充要条件[J].四川师范大学学报(自然科学版),1997,20(4):15-19.
[5]蒋加清.对称r—循环矩阵求逆的初等变换算法 [J].吉林师范大学学报(自然科学版),2013,34(3):63-65.
[6]蒋加清.用辗转相除法求循环矩阵的逆矩阵[J].数学理论与研究,2011,31(3):123-128.
Study on Calculating Inverse Matrices of Symmetric Skew-Cyclic Matrices
JIANG Jia-qing
(School of Teacher Education,Taizhou University,Linhai 317000,China)
It has a practical applicability to adopt a solution to get the anti-Symmetric Skew Cyclic Matrices (SSCM)with the method of lines of elementary transformation,using the generating polynomial and characteristic polynomial by the nature of SSCM.
building a matrix;symmetric skew cyclic matrices;diagonal matrices;generating polynomial;reversibility;elementary row operation.
10.13853/j.cnki.issn.1672-3708.2014.06.002
(责任编辑:耿继祥)
2014-06-12;
2014-07-13
蒋加清(1960- ),男,浙江临海人,从事高等代数教学与研究。
