齿轮箱状态识别与剩余寿命预测的MoG-BBN法

张星辉，李凤学，赵劲松,2，曹端超，滕红智

（1.军械工程学院，石家庄 050003；2.军事交通学院，天津 300161；3.68129部队，兰州 730060）

CBM(Condition Based Maintennce)主要利用状态监测数据（油液、温度、振动信号等）对设备的故障状态和剩余寿命（Remaining Useful Life，RUL）做出判断，在此基础上对后续的维修进行决策。在整个CBM实施过程中，设备的状态识别和RUL预测是基础[1]。近年来，隐马尔可夫族模型（Hidden Markov Models，HMMs）在状态识别和RUL预测领域得到广泛应用[2―5]。文献[6]应用混合高斯输出HMM对轴承的退化状态进行识别并预测RUL。与HMM相比，贝叶斯信念网络（Bayesian Belief Networks，BBN）模型结构更易于扩展，既能进行单部件状态识别和RUL预测，也可以对包含多个部件的复杂设备进行状态识别和RUL预测[7―10]。借鉴混合高斯输出HMM的模型结构，可以构建与之有相同功能且结构更为简化的混合高斯输出贝叶斯信念网络（Mixture of Gaussian Bayesian Belief Networks，MoG-BBN）。状态识别和RUL预测都需要提取相应的特征。其中，状态识别需要提取能够区别各种退化状态的退化特征向量，该特征向量由时域特征、频域特征和时频域特征中的一种或者多种共同组成。而RUL预测需要提取能够反映设备全寿命退化过程的特征量[11]。目前，如何合理划分设备的劣化状态并提取有效的全寿命过程退化特征还需要进行更为深入的研究，以便为状态识别和RUL预测乃至维修决策提供重要支持。本文应用小波包分解[12,13]，提取用于状态识别的故障特征向量，在此基础上应用聚类指标对退化状态进行优化，确定最优的退化状态数目后，从故障特征向量中挑选能够反映设备全寿命退化过程的量，并采用趋势项提取法对趋势项进行提取。最后，在状态识别的基础上，应用提出的RUL预测公式结合退化特征对RUL进行预测。

1 MoG-BBN基本原理

BBN是一种概率推理网络，它以图形节点表示随机变量，节点之间的有向箭头表示随机变量之间的因果关系。BBN是一个在不确定条件下强有力的知识表达和推理方法。BBN中节点所代表随机变量的取值可以是连续的，也可以是离散的。连续变量可以服从任意分布，离散变量的取值可以是两个或多个。本文构建的MoG-BBN模型，其网络结构如图1所示：

图1 贝叶斯信念网络

该模型可以用如下参数描述：

（1）X表示隐状态，状态取值分别为1,2,…,K，代表齿轮箱的故障模式；

（2）M表示混合数，取值范围为1,2,…,m，代表齿轮箱的某个故障模式按照第m个高斯分布产生观测值；

（3）Y表示观测值，

在图1所示的贝叶斯网络中，X是根节点（M和Y的父节点），M是中间节点（X的子节点，Y的父节点），Y是叶节点（X和M的子节点）。

2 基于MoG-BBN的状态识别与RUL预测

设备从正常到失效要经历一系列不同的退化状态，这些状态通常不能直接观测，但可通过外部测量（振动信号等）判断内部状态。通常，利用MoG-BBN对设备退化过程实施状态识别和RUL预测包括三个关键步骤：确定退化状态数目、状态识别和RUL预测。

2.1 退化状态数目优化

确定设备退化状态数目是利用MoG-BBN进行状态识别和RUL预测的前提。多数文献都是靠经验来确定退化状态数目。董明根据油液的污染度将泵轴承分为四个退化状态[14]。文献[15]在应用HMM预测时，假设设备的退化状态数目为2（好和坏）。退化状态数目的确定大致可以分为三种方法：

一是由专家根据经验确定；二是利用交叉验证思想以分类器的分类错误率最低来确定；三是应用聚类方法评价指标确定。由于设备的构造越来越复杂，由专家根据经验来确定退化状态数目缺乏通用性，且需要大量的实验，对于高可靠、价格昂贵的部件并不适用。利用交叉验证的思想确定最优退化状态数目需要对不同的退化状态数目训练分类器并检验其分类错误率，计算时间长，效率低[5]。而应用聚类方法评价指标确定最优退化状态数目则简便易行，计算效率高。

聚类方法评价指标分别为：

分割系数[16]（Partition Coefficient，PC），定义为

图2 基于MoG-BBN的退化状态识别框架

以上表达式中μij表示第j个样本属于第i类的概率，xj表示第j个样本，vi表示第i类的聚类中心，vk表示第k类的聚类中心，1≤i，k≤c，c表示聚类数目，N表示样本数目。其中，PC取值越大越好，SC、SI和XB取值越小越好。

2.2 基于MoG-BBN的退化状态识别

i为初始退化状态，j为t（当前）时刻退化状态。

2.3 基于MoG-BBN的RUL预测

当获得退化状态序列H后，通过求取退化状态信息即可进行RUL预测。往往同型号的多个设备其退化过程也不尽相同，当其退化量超过某一预先确定的阈值时，设备失效。对其进行RUL预测，也就是预测从当前退化量到达退化量阈值所需的时间。

定义如下退化状态信息

通常，设备真实的退化量是无法测量的。因此，在实际计算过程中，可以从提取的特征向量中，选取全寿命过程中某一特征作为设备退化量的度量。

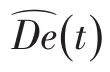
RUL的值即可表示为退化量阈值Dlimit与现有退化量的差值。

3 实验及数据分析

3.1 实验设置

实验设备如图3所示，实验所用齿轮箱型号为JZQ175；动力源为电磁调速电机，型号为YCT180-4A；风冷磁粉制动器为齿轮箱提供载荷，型号为FZ200.K/F。齿轮箱参数及传感器位置如图4所示。该实验为全寿命实验，为缩短实验时间，齿轮箱传递功率为额定功率的2～2.5倍，转速为1 200 r/min，输入端负载为15 N∙m，采样频率为20 kHz，采样时间为6 s

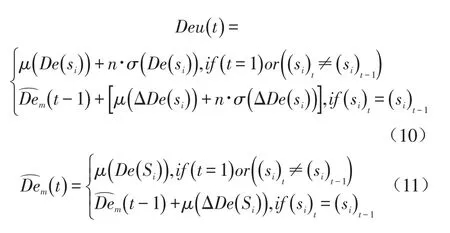
图3 实验台示意图

图4 齿轮箱结构及传感器位置

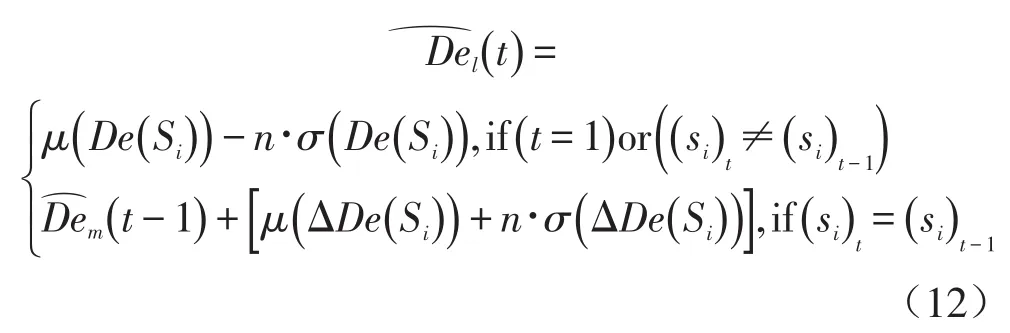
每10 min钟采集1组数据。实验发现，齿轮箱工作548 h后失效，主要故障形式是齿面严重磨损和断齿，如图5和6所示。

实验采集的是加速度信号，共3 288组数据。用‘db 8’小波分别对四个通道的振动信号进行小波包3层分解，提取各频带能量作为特征向量。因此，四个通道共32个特征，特征矩阵F的维数为3 288×32。

3.2 基于MoG-BBN的状态识别

（1）状态数优化

图5 齿轮箱实验中期1号齿轮严重磨损

图6 齿轮箱实验后期1号齿轮失效

首先应用K均值聚类算法对特征矩阵F进行聚类，聚类数目取2～7。然后分别计算PC、SC、SI、XB的值。结果如图8所示。从图中可以看出，最佳的聚类数目为3。因此将齿轮箱全寿命过程分为3个退化状态。最后，应用K均值聚类算法将特征矩阵聚为3类，获得类别序号及聚类中心向量。

（2）MoG-BBN分类器训练

从第1类中选取类别序号401～450所对应的特征矩阵；从第2类中选取类别序号3 091～3 130所对应的特征矩阵；从第3类中选取类别序号3 279～3 288所对应的特征矩阵。3个类别共100组数据用来训练MoG-BBN分类器。分类器的初始参数设置和训练后的参数如表1所示，由于混合高斯分布的均值和方差维数较大，在表中不列出。

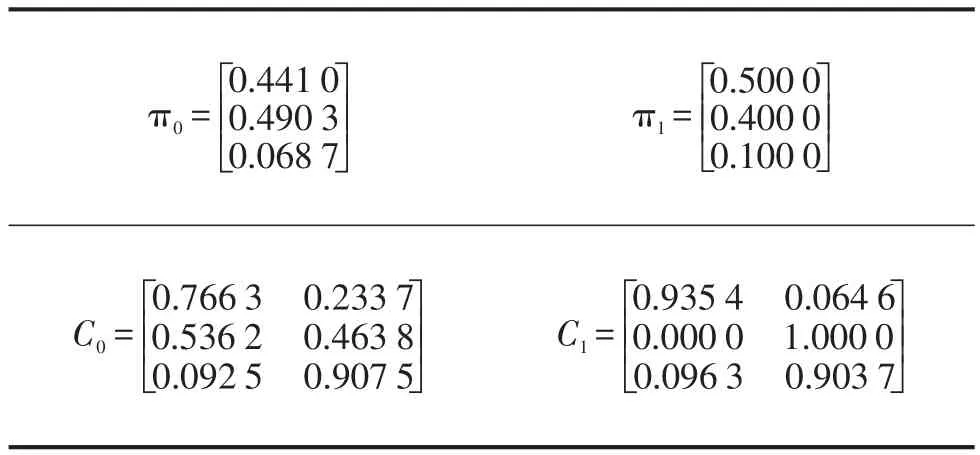
表1 MoG-BBN初始及训练后参数

（3）齿轮箱全寿命过程状态识别

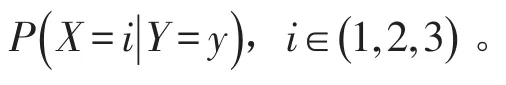
3.3 基于MoG-BBN的RUL预测

图7 齿轮箱退化量度量指标

根据式（5）—（8）可求得退化参数如表2所示。计算公式（10）—（12）中的n∙σ表示3 Sigma准则（68%，95%，99.7%）。在该实验中选取n=3。RUL预测正确率计算公式为

表2 估计的退化参数值

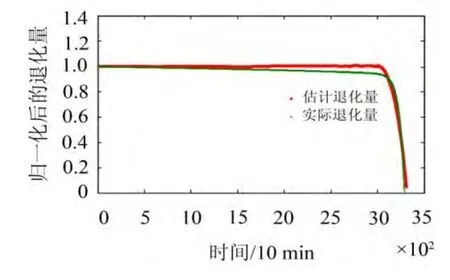
图8 齿轮箱RUL预测结果

4 结语

本文建立了基于MoG-BBN的齿轮箱状态识别和RUL预测框架和计算方法，采用聚类评价指标的状态数优化方法，与交叉验证的状态数优化方法相比，其运算速度快，计算简洁。齿轮箱全寿命实验验证了论文所用方法的有效性，平均预测准确率达到了96.47%，为齿轮箱的健康管理提供了科学依据，也为其它类型设备的状态识别和RUL预测提供了借鉴。

[1]Jardine A K S,Lin D and Banjevic D.A review on machinerydiagnosticsand prognosticsimplementing condition based maintenance[J].Mechanical Systems and Signal Processing,2006,20:1483-1510.

[2]Boutros T,Liang M.Detection and diagnosis of bearing and cutting tool faults using hidden Markov models[J].Mechanical Systems and Signal Processing,2011,25:2102-2124.

[3]Lee J M,Kim S J,Hwang Y and Song C S.Diagnosis of mechanical fault signals using continuous hidden Markov model[J].Journal of Sound and Vibration,2004,276:1065-1080.

[4]V.Purushotham,S.Narayanan,S.A.N.Prasad.Multifault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition[J].NDT&E International,2005,38:654-664.

[5]滕红智，赵建民，贾希胜，张星辉，王正军.基于CHMM的齿轮箱状态识别研究[J].振动与冲击，2012，31(5)：92-96.

[6]Tobon D A-Mejia,Medjaher K,Zerhouni N and Tripot G.A data-driven failure prognostics method based on mixture of Gaussians hidden Markov models[J].IEEE Transactions on Reliability,2012,61(2):491-503.

[7]Xu B G.Intelligent fault inference for rotating flexible rotors using Bayesian belief network[J].Expert Systems withApplications,2012,39:816-822.

[8]Dey S,Stori J.A Bayesian network approach to root cause diagnosis of process variations[J].International Journal of Machine Tools and Manufacture,2005,45:75-91.

[9]Verron S,Li J and Tiplica T.Fault detection and isolation of faults in a multivariate process with Bayesian network[J].Journal of Process Control,2010,20:902-911.

[10]Sahin F,Yavuz M C,Arnavut Z and Uluyol O.Fault diagnosis for airplane engines using Bayesian networks and distributed particle swarm optimization[J].Parallel Computing,2007,33:124-143.

[11]Gebraeel N,Lawley M,Liu R and Parmeshwaran V.Residual life predictions from vibration-based degradation signals:a neural network approach[J].IEEE Transactions on Industrial Electronics,2004,51(3):694-700.

[12]齐子元，米东，徐章隧.小波多分辨率分析的频带阈值去噪方法[J].噪声与振动控制，2008，4：130-134.

[13]雷正伟，米东，徐章隧，敦 怡.基于小波谱分析的导弹发动机复合材料深层缺陷检测[J].噪声与振动控制，2007，1：45-47.

[14]Dong M,He D.A segmental hidden semi-Markov model(HSMM)-based diagnostics and prognostics framework and methodology[J].Mechanical Systems and Signal Processing,2007,21:2248-2266.

[15]Zhou Z.J,Hu C H,Xu D L,Chen M Y,Zhou D H.A model for real-time failure prognosis based on hidden Markov model and belief rule base[J].European Journal of Operational Research,2010,207:269-283.

[16]Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].Plenum Press,1981.

[17]Bensaid A M,Hall L O,Bezdek J C,Clarke L P,Silbiger M L,Arrington J A and Murtagh R F.Validity-guided clustering with applications to image segmentation[J].IEEE Transactions on Fuzzy Systems,1996,4:112-123.

[18]Xie X L,Beni G.A validity measure for fuzzy clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991,13(8):841-847.

[19]Shao Y,Nezu K.Prognosis of remaining bearing life using neural networks[C].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2000:217-230.

[20]Gebraeel N,Lawley M,Liu R and Parmeshwaran V.Residual life predictions from vibration-based degradation signals:A neural network approach[J].IEEE Transactions on Industrial Electronics,2004,51:694-700.