熔融碳酸盐燃料电池与斯特林热机耦合系统的性能优化分析

陈礼炜

(三明学院 机电工程学院，福建 三明 365004)

熔融碳酸盐燃料电池与斯特林热机耦合系统的性能优化分析

陈礼炜

(三明学院 机电工程学院，福建 三明 365004)

建立一个主要由熔融碳酸盐燃料电池（MCFC）和斯特林热机组成的新型耦合系统，其中斯特林热机是由在MCFC中产生的高品质废热驱动的。基于电化学和非平衡热力学，考虑各种不可逆损失的影响得到了耦合动力系统的效率和功率输出的解析表达式。研究表明，MCFC的性能可以通过耦合斯特林热机以进一步将废热转化为电输出而大幅度提高。此外，采用数值计算，不仅分析了多个不可逆损失对耦合系统性能的影响，并且还讨论了一些工作条件比如工作温度、输入气体组合以及工作压强对耦合系统性能响。

熔融碳酸盐燃料电池；斯特林热机；耦合系统；性能优化分析

21世纪人类面临的最主要的考验是全球化的能源、环境和经济问题，其中能源属于重中之重。在与生活息息相关的电能问题上，由于燃料价格的上涨、越来越严峻的环境问题、以及现在的和未来的环保法规，在使发电运行有更好的效率、成本效益和环保方式上有了越来越大的压力。由于燃料电池高效率和零有害气体排放水平，它具有替代传统的发电厂的潜力[1-3]。燃料电池能够被应用到工业用热电联供、家用热电联供系统、集中型大规模电源、分散型中小规模电源、潜水艇、汽车、IT器械、移动式燃料电池发电机等方面。在现有的燃料电池技术之间[4-6]，MCFC作为典型的高温燃料电池，由于它的燃料灵活性、高效率和高废热而展露出极好的前景[7-9]。MCFC释放的高质量废热有利于热电联产与和其它类型的发电机，比如热机和微型燃气轮机，组合构成联合发电设备[10-13]。

因为难以实验量化其相关参数管理的耦合系统，所以理论建模和数值分析成为优化系统设计和工作条件必不可少的步骤。许多学者开展了以MCFC为基础的耦合系统的数值分析研究[12,-17]。有一部分学者从理论上模拟各种MCFC热发动机混合动力系统，并评估和优化耦合系统的性能[5-6,12-13]。另一些学者根据不同观点和不同规模水平以不同的方式建立以MCFC为基础的耦合系统模型[4,14-17]，获得的结果为实际的MCFC基础混合模型的发展提供一定的理论基础。最近，Rokni[18]发表了关于使用固体氧化物燃料电池和斯特林混合工厂替代燃料的热力学分析报告，发现使用耦合系统生产的全部电力比单独的固体氧化物燃料电池工厂增加了大约10%。在众多数量饱和的发电机中，因为其结构简单、制造是一样的往复式内燃机，斯特林热机以其无可比拟的优势成为当之无愧的首选。斯特林发动机将获得大规模经济效益，并可以建立一个廉价的电力来源[1-8,20]。使用MCFC获得机械能时直接转换的废热通过斯特林热机以进一步利用不仅能降低生产成本，还可以减少制造复杂性。

在本论文中，建立了一个MCFC-斯特林热机耦合系统的不可逆热力学电化学模型，其中不仅考虑了MCFC内部的不可逆损失，而且还考虑了包括从燃料电池到环境中的热漏，以及燃料电池和热机之间的热传递等。根据热力学和电化学分析，推导了混合动力系统的效率和输出功率等一些关键性能参数的新表达式，以此揭示了耦合系统的一般性能特性给出了一些重要的性能参数的最优区域中，探讨了一些不可逆的损失因素和工作条件对混合动力系统的性能的影响，优化了混合动力系统中性能特性。本文所得的结果可为实际MCFC-斯特林热机的混合动力系统的初步概念设计和实际运行提供理论帮助。

1 MCFC-斯特林热机耦合系统模型

MCFC-斯特林热机耦合系统主要由一个MCFC，一个斯特林热机和一个回热器组成，如图1所示。在耦合系统中，MCFC扮演着斯特林热机的高温热源的角色，斯特林热机将MCFC内部产生的废热进一步利用而转化成输出功。回热器相当于一个逆流换热器，它合理的吸收热量使高温废气预热反应物达到反应温度。

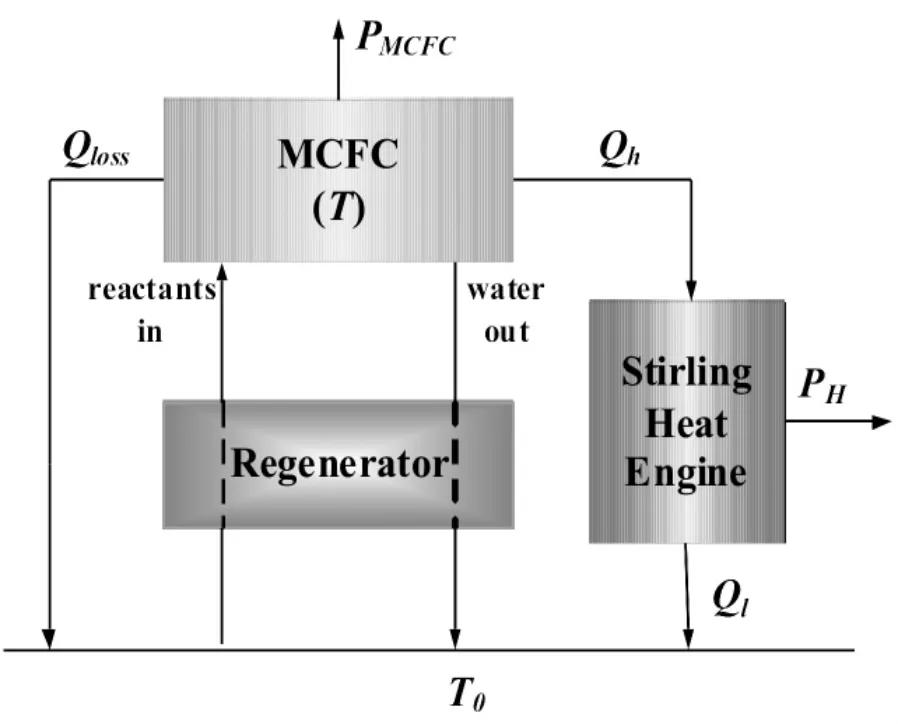
图1 MCFC-斯特林热机耦合系统的示意图

为了分析整个动力系统的性能，通常主要采用以下假设[7-8,12,20-21]：

（1）MCFC和斯特林发动机都是在稳定状态条件下工作；

（2）MCFC中的工作温度和压力均匀并保持为常数；

（3）所涉及的所有气体被认为是理想的可压缩气体；

（4）化学反应是完整的并且反应后不剩余反应物。

在这些假设的帮助下，可以得到混合动力系统的性能参数的表达式。因此将分别分析所述耦合系统中的每个组件，然后研究整个耦合系统的性能特征。

1.1 MCFC模型

本次研究中提出的MCFC模型在之前的文献已有报道[5]。如图2所示，产生的二氧化碳从阳极运输到阴极，同时产生的碳酸根离子从阴极流向阳极。为了维持整个电化学反应的持续运行，氢气和氧气应分别连续不断地提供给阳极和阴极。总的电化学反应是：

其中下标“an”和“cat”分别表示阳极和阴极。为了定量地描述MCFC的电化学反应，很重要的一点是要理解燃料电池的热力学工作原理，其基本的热力学关系可以表达为[5,12]：

其中ne表示电子数量，F是法拉第常量，j指电流密度，A表示MCFC的极板面积，Δh是摩尔焓变并且可以通过下面的表1计算得到[5]。根据基本热力学关系：-ΔH=-ΔG-TΔS，总的变化-ΔH可以分成两个部分，那就是-ΔG和-TΔS，它们分别代表反应释放的电能和热能。只要反应中负的焓变多于Gibbs自由能的变化，总能量中不能转化成电能的一部分就会以热能释放。通过Yuh和Selman成熟的凝聚模型[21]，MCFC的输出功率和效率可以分别表示为[5]：

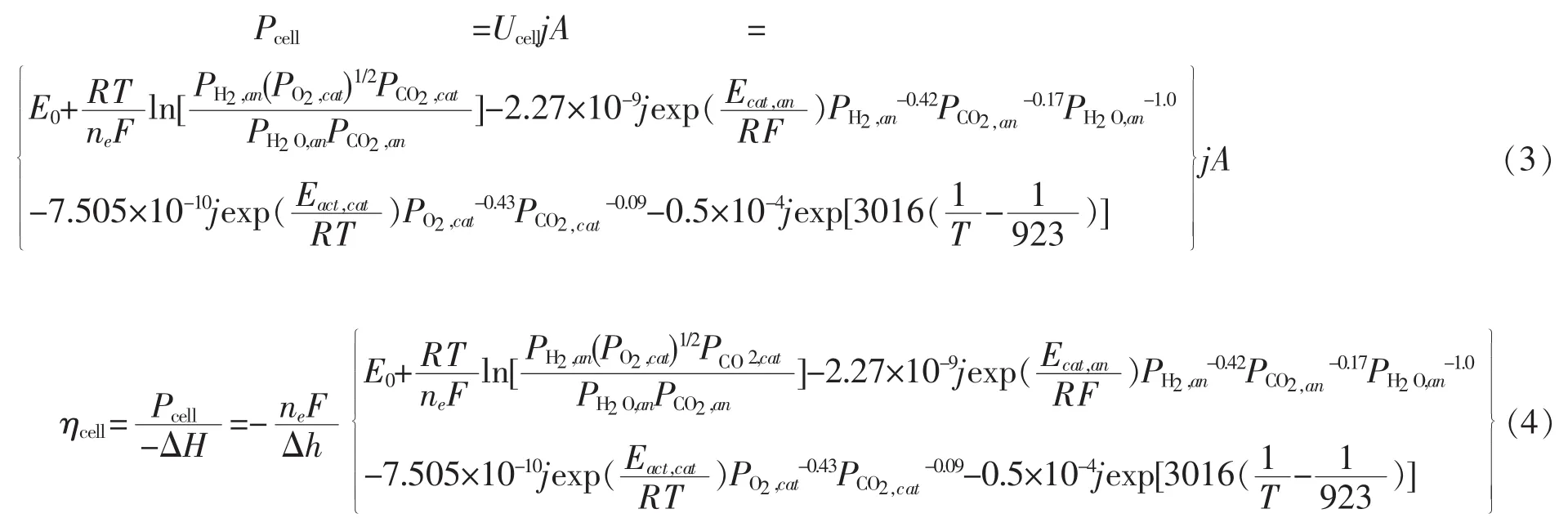
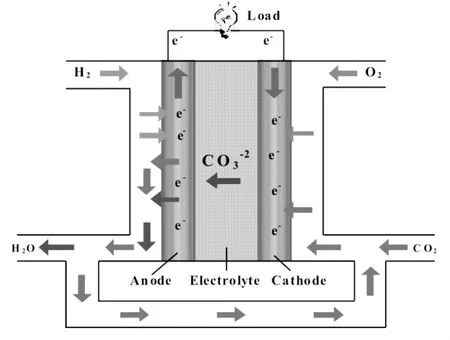
图2 MCFC的简略示意图

其中E0=-是理想的标准电势，ΔG=-242000.0+45.8T[22]；R是普适气体常数；Ecat是活化能，pk为k在阳极和阴极的分压。

表1 在1个大气压下反应物/产物的热力学参数

1.2 回热器

回热器是常见的蓄冷部件。如图1所示，回热器在混合动力系统中作为热量交换器工作，利用燃料电池的高温出口气将入口的反应物从室温加热到电池温度，完成系统的冷、热交换功能。由于热电阻的存在，蓄热损失是不可避免的，而且通常认为回热损失是和燃料电池与环境之间的温差成正比，即：

其中kre是传热系数，ε表示回热器的效率。有了回热器的帮助，燃料电池和因此组成的整个混合动力系统可以确保在稳态条件下正常并且连续地工作。

1.3 斯特林热机

斯特林循环作为标准空气循环热机的其中重要一种[10,23]，已经被广泛地应用到各个领域。它的主要优势是，循环可以由各种各样的燃料驱动，并且它提供了高效发电的可能[10,23-24]。如图3所示，斯特林循环分别由两个温度为T1和T2的等温过程和两个容积为V1和V2的等容过程组成。对于实际的斯特林热机，工作物质和热储层之间的热电阻是不变的。因此，热力学限定时间被选择作为强有力的工具用来描述真实发动机的多元不可逆性。对于一个给定的输入热量qh，考虑热机中的有限热传导率和实际回热不可逆拟因素，那么最大效率可以表示为[10]：

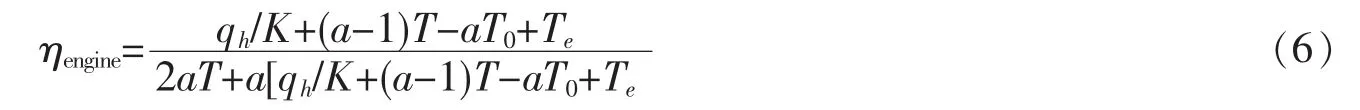
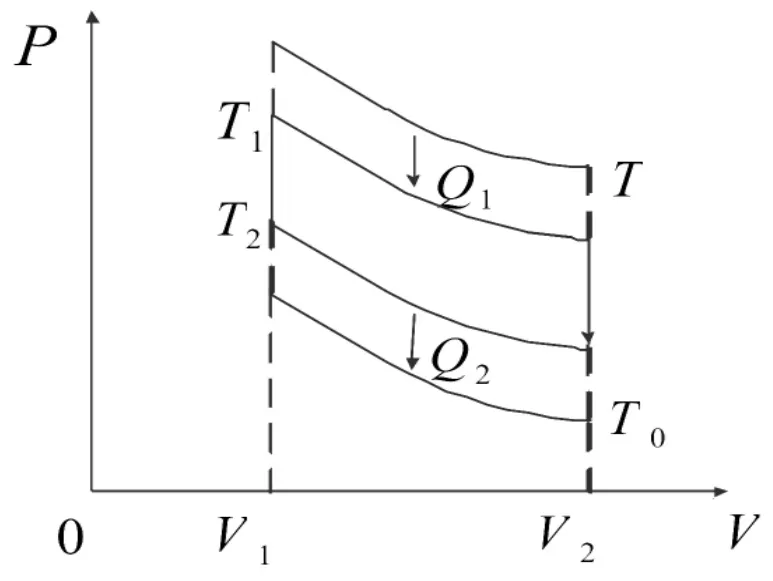
图3 斯特林循环的P-V图

其中 a=xC/[Rln(V2/V1)指热机中的不可逆有限热传导率，Te={[(a+1)T+aT0-qh/K]2-4a(a+1)TT0}0.5， K=k1/[(1+b),x是理想回热中的一部分误差，b是等温分支中的回热部分的时间比例，C是每摩尔参与回热过程的工作物质的热容量，k1和k2分别是在温度T（MCFC排气温度）和T0（环境温度）时工作物质和热源之间的热导率。

如图1所示，燃料电池产生的其中一部分废热是通过热传递直接释放到环境中，这里的热总量可以由式(7)给出[15-16]：

其中α表示对流热传递系数，Al表示有效的热转移面积。结合前面的分析，从MCFC到斯特林热机的废热流率可表示为

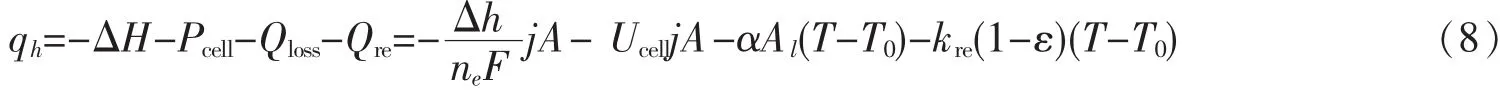
将式（8）代入到式（6）中，斯特林热机的优化效率和输出功率可以分别表示为

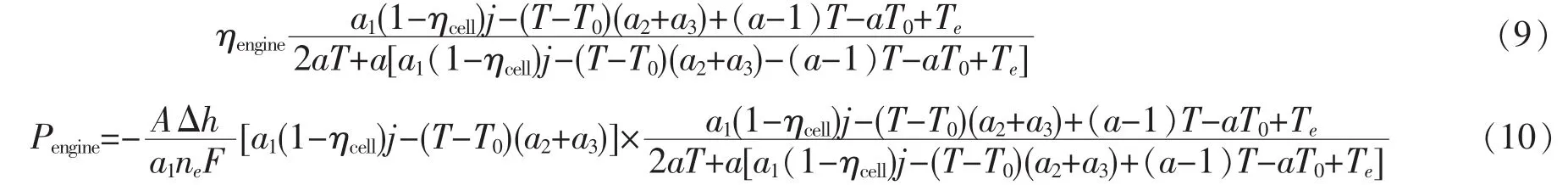
其中a1=-是指系统结构的综合参数，a2=和a3=(1-ε)是分别用来描述从燃料电池到环境中的热传递影响和耦合系统中回热器的实际回热性能的两个参数。

1.4 耦合系统的效率和输出功率

应该提及的是，整个系统中的有效热能等于整个电化学反应的焓变，即，Qall=-ΔH[19]。通过方程式（3），（4），（9）和（10），可以得到整个MCFC-斯特林热机耦合系统的效率和输出功率，即，

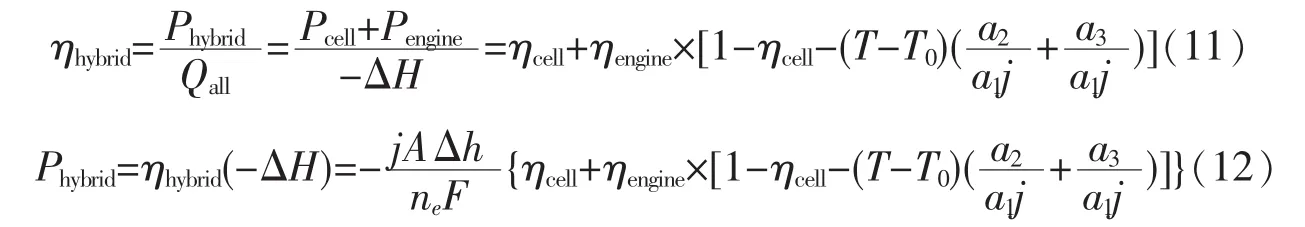
从等式（11）和（12）可以看出，耦合系统的效率和输出功率要大于单独的MCFC，并且效率和输出功率紧密依赖于包括在燃料电池自身内部的不可逆性以及来自MCFC与斯特林热机之间的热传递的不可逆性。

2 一般性能特征和最优特性

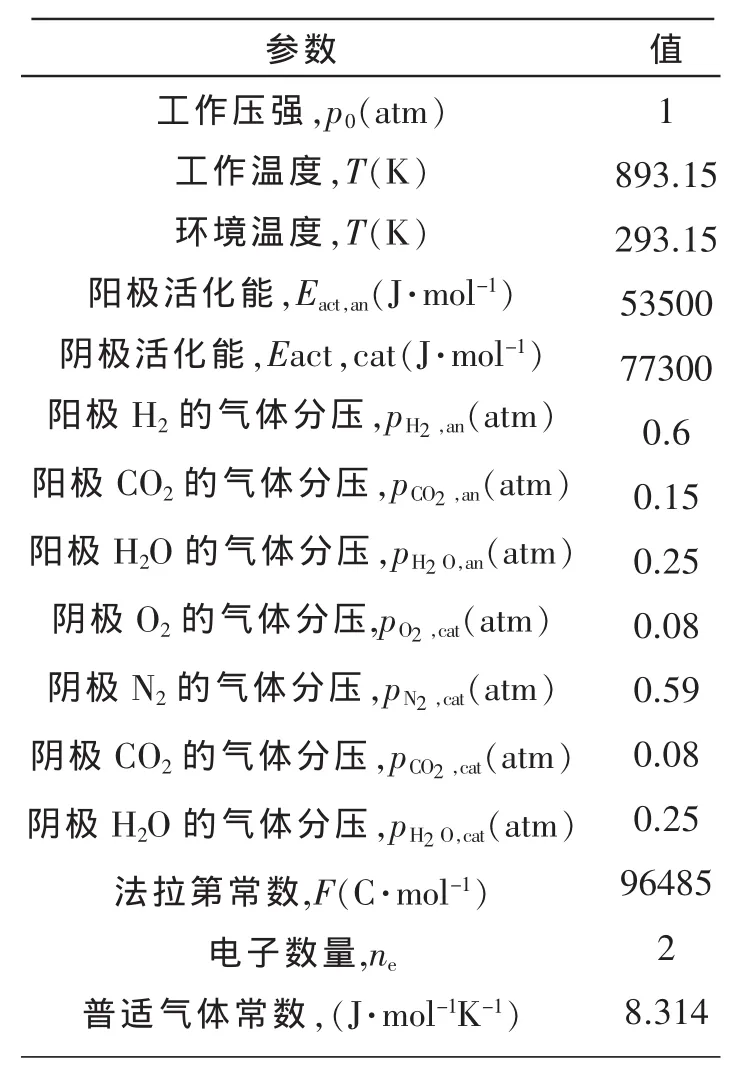
表2 在模型中使用到的参数

耦合系统的最佳的设计和分析需要彻底地了解其性能的界限。公式（11）和（12）清晰地表明了耦合系统的性能依赖于一系列热力学和电化学参数，比如燃料电池温度（T）和环境温度（T0），工作电流密度（j），以及与MCFC和斯特林热机之间的热传递、与环境间热漏相关的参数，即a，a1，a2和a3。在接下来的计算中，阳极的气体组成成分是60%H2+25%H20+15%CO2，阴极的气体组成成分是8%O2+59%N2+8%CO2+25%H20，其中的参数取以下值a=0.01，a1=0.103KA-1m2，a2=0.008和a3=0.005。其他没有提及的输入参数的相关值归纳在表2中[5,7]，除非特别提及，否则这些参数都是保持常量。

通过等式（11）和（12），可以得到MCFC、斯特林热机和耦合系统的效率和功率密度随电流密度的变化曲线，如图4所示，其中的P*=P/A为功率密度。从图4中可以清晰看出随着电流密度的增加，耦合系统的效率和功率密度先增加后减少，并且这里存在一个最大的效率ηmax和一个最大的功率密度P*max，其中的jη和jP*分别为在最高效率ηmax和最高功率密度P*max时相对应的电流密度。相比于纯MCFC的效率和功率密度，耦合系统的效率和功率密度有了显著提高，因为利用了燃料电池的废热。当j＜jη时，效率和功率密度随着电流密度的增加而增加，然而当j＞jP*时，效率和功率密度却随着电流密度的增加而减少。很明显从热力学的观点来看j＜jη和j＞jP*并不是最佳的区域，尽管在这些区域中耦合系统同样可以工作。因此，最佳的电流密度应该处于

这表示jη和jP*分别确定了最佳电流密度的下限和上限。在MCFC-斯特林热机耦合系统的实际运行中，工程师应该根据方程式（13）选择合理的电流密度以确保系统处于最佳区域进行工作。图5显示了在不同工作温度下的功率密度随效率的变化曲线，其中的P*m和ηm分别是在最高效率ηmax时的功率密度和在最高输出功率P*max时的效率。根据图5，可以确定一个最佳工作区域，那就是曲线η-P*中具有负斜率的一部分。当耦合系统在这个区域内工作，功率密度会随着效率的增大而减小，反之亦然。因此，效率和功率密度的最佳范围分别是

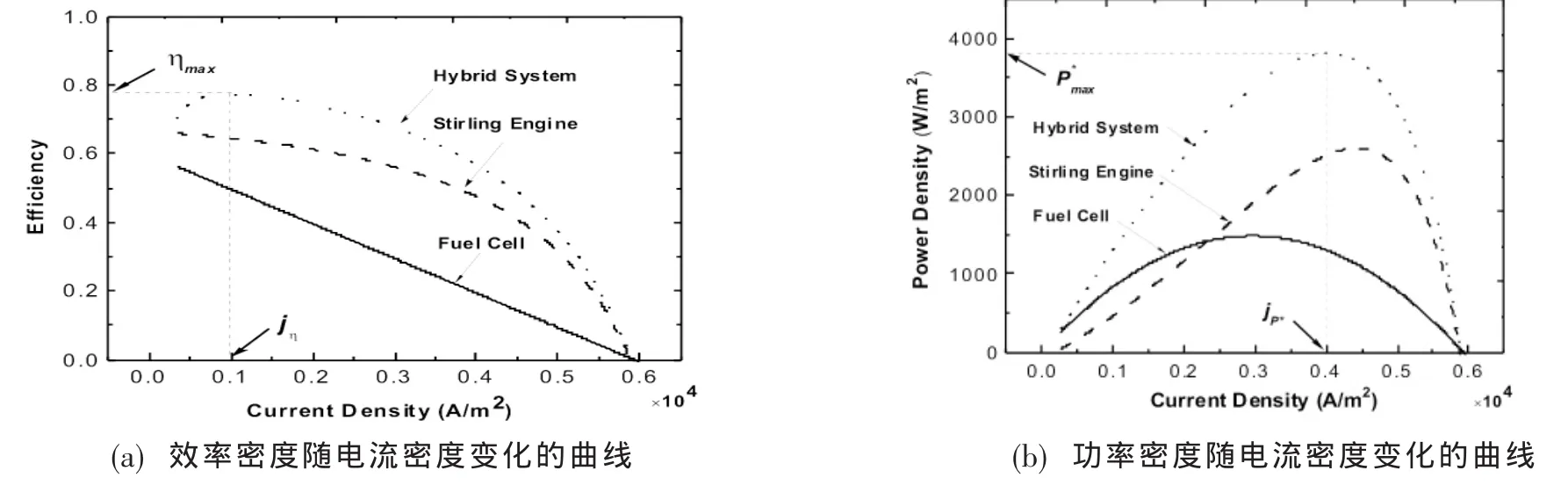
图4 η-P*随电流变化曲线

上面的结果表示P*m，ηm，P*max和ηmax是MCFC-斯特林热机耦合系统的4个重要的参数，这里的P*m和ηm确定了得到功率密度和效率最佳值允许的下限，而P*max和ηmax则是最佳值允许的上限。需要注意的是，这4个重要参数密切依赖于混合动力系统的热力学和电化学参数，并且可以根据提供的其它参数值而进行定量地计算。

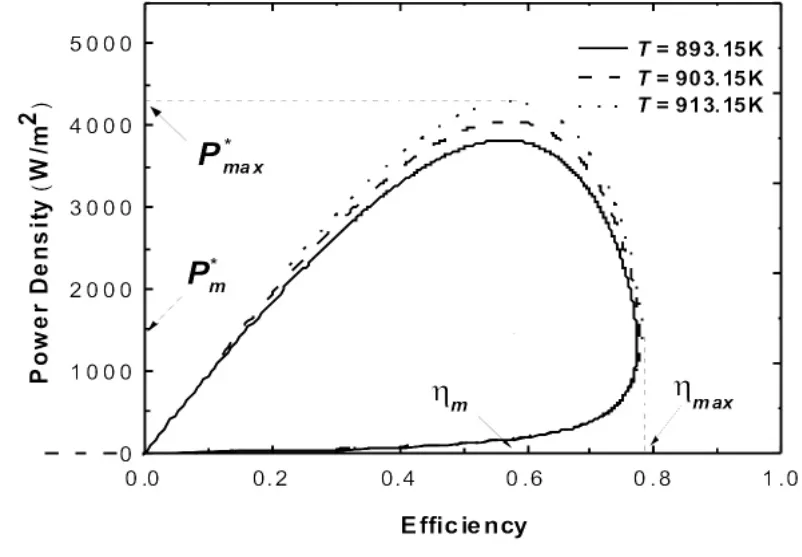
图5 在不同工作温度下功率密度随效率变化的曲线

3 结果与讨论

值得注意的是，开发的系统模型可以用来研究各种工作条件对混合动力系统性能的影响。在本节中，基于工作条件变化时的性能标准的参数分析来描述系统的性能。

3.1 工作条件的影响

如同等式（11）和（12）所表示的，混合动力系统的性能密切相关于各种工作条件比如工作温度，阳极或阴极的分压，以及工作压力。此外还将分别讨论环境温度T和混合动力系统入口反应物的温度Ti对系统性能的影响。系统的环境温度是一个重要参数，因为它能直接影响燃料电池的各种过电势和耦合系统的性能。如图6～7所示，MCFC-斯特林热机耦合系统的功率密度和效率工作的温度范围是873～973 K，电流密度范围是0～6000 A·m-2，这里的环境温度T0=298.15 K选择为。就像图6和图7所展示的，系统的性能随着环境温度的上升也会提高。与此同时，最高效率、最大功率密度以及相应的电流密度都会随着环境温度的上升有轻微的提高。一般地，混合动力系统入口反应物的温度Ti通常高于环境温度T0，因为提供给系统的反应物是高度压缩的，并且假定当提供的反应物是一个大气压时与环境温度是相等的[12]。反应物的低入口温度可能会降低MCFC的工作温度，并且较低的工作温度也会恶化耦合系统的性能，因此，很容易预测，耦合系统的性能将随着T的增加或者Ti的提高而改进。此外，对于怎么选择系统的工作温度这个问题，可以同时考虑涉及到制造MCFC所需的热稳定性以及整个系统可以在指定温度运行的投资成本和退化问题。系统的效率会随着工作温度的上升而增加，与此同时，最高的效率和相应的电流密度也会因为工作温度的上升而轻微增加。

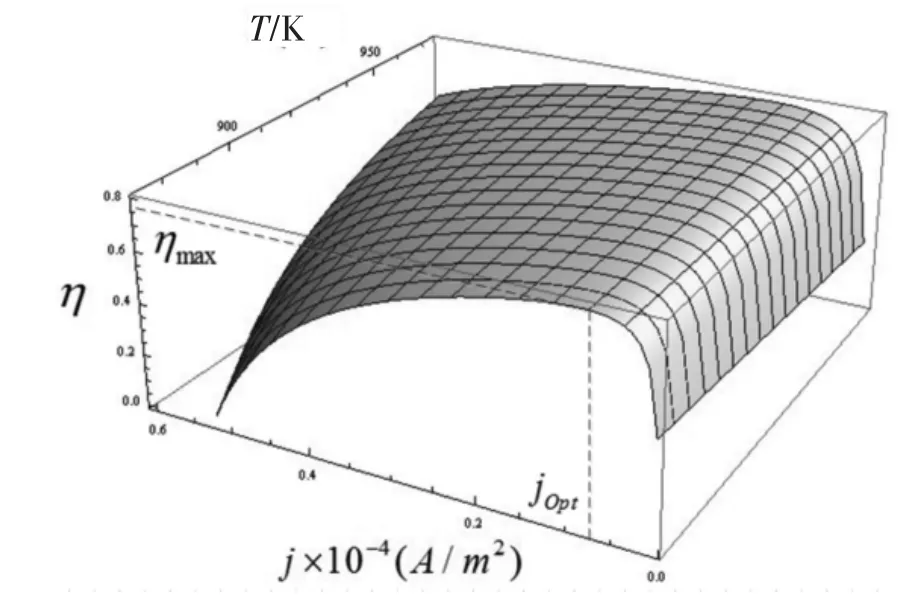
图6 效率随电流密度和温度变化的三维曲线

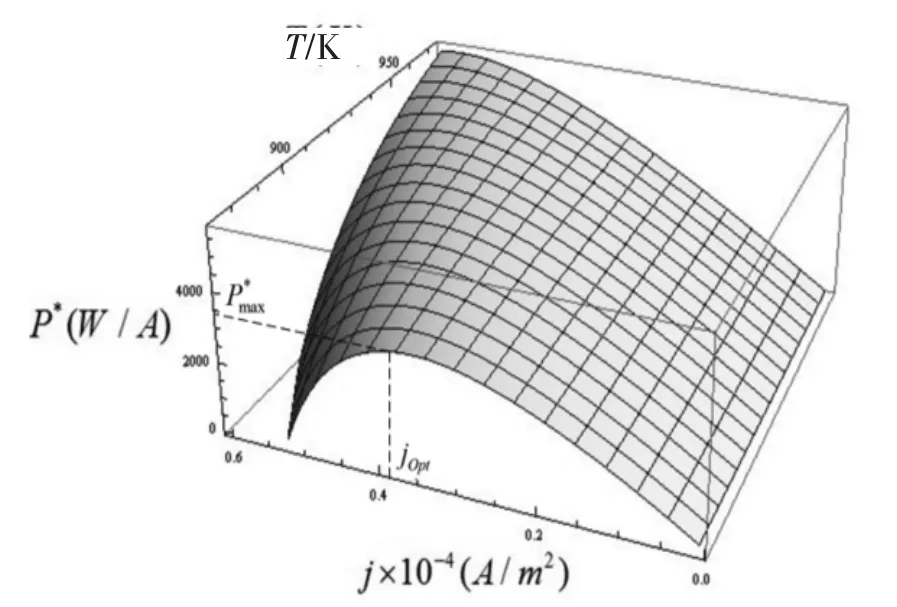
图7 功率密度随电流密度和温度变化的三维曲线

众所周知，阳极和阴极的气体分压会强烈地影响耦合系统的性能，如图8所示。从图8中可以看出，阳极H2和H2O的不同分压将导致功率增加、效率下降，或者此相反。然而，随着阴极处O2和CO2的分压增大，效率和功率密度都会增加。这种现象可以如此解释：O2和CO2的浓度增加将导致更高的化学反应速率，从而导致系统性能的净增加。

此外，气体的工作压强也可以对系统性能产生很大的影响。如图9所示，工作压强越大，性能越好。然而，工作压强的增加势必带来额外的电能消耗。因此，合理选择工作压强是在耦合系统中非常重要的实际工作。工作压力越大，分子之间的距离越小，相应地，在较大的工作压强条件下化学反应速率也会加强。从本质上讲，通过提高工作压强的方法来提高性能是和通过增加反应物浓度一样的。

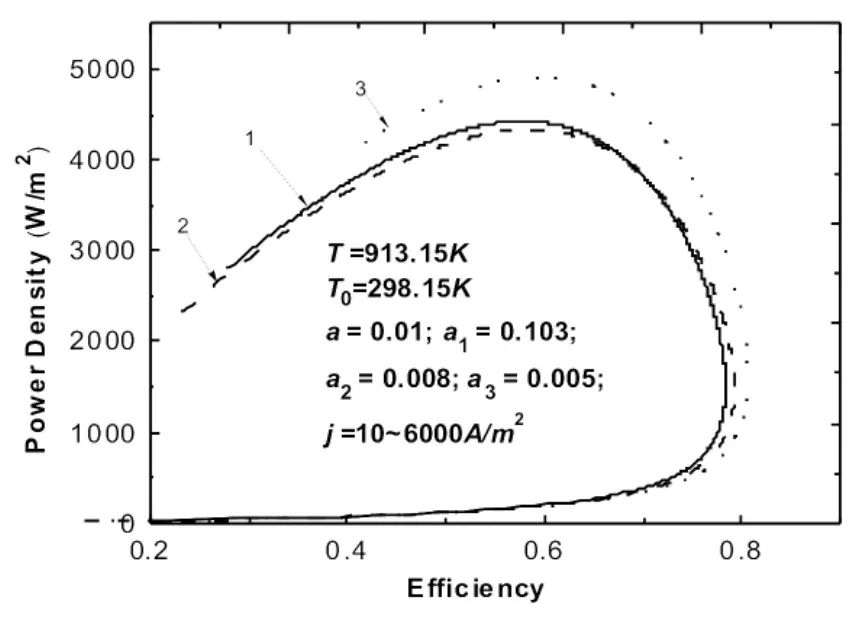
图8 在阳极和阴极不同的气体分压下功率密度随效率变化的曲线

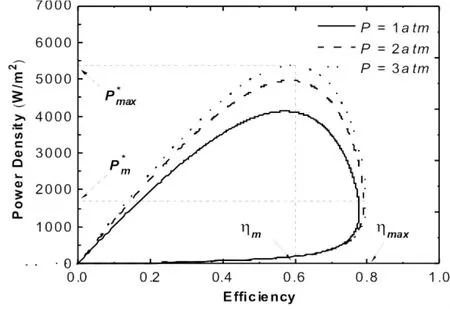
图9 在不同气压条件下功率密度随效率变化的曲线

3.2 性能的上限

获得耦合系统性能的上限是一个有趣的问题。如果斯特林热机是可逆的，MCFC和热漏损失和回热器的回热损失可以忽略不计，即a=a1=a2=a3=0，公式（11）和（12）可以分别简化为

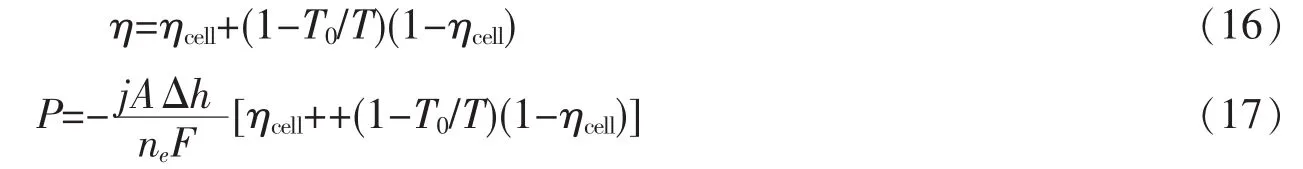
如图10所示，黑色曲线表示性能的范围，其中P0*max和η0max分别表示耦合系统可能到达的最大功率密度和最高效率，η0,m是与P0*,m相对应的效率。当选择不同的参数值a,a1,a2,a3，系统的性能范围会有所不同，图10中的黑线代表了耦合系统的性能极限。

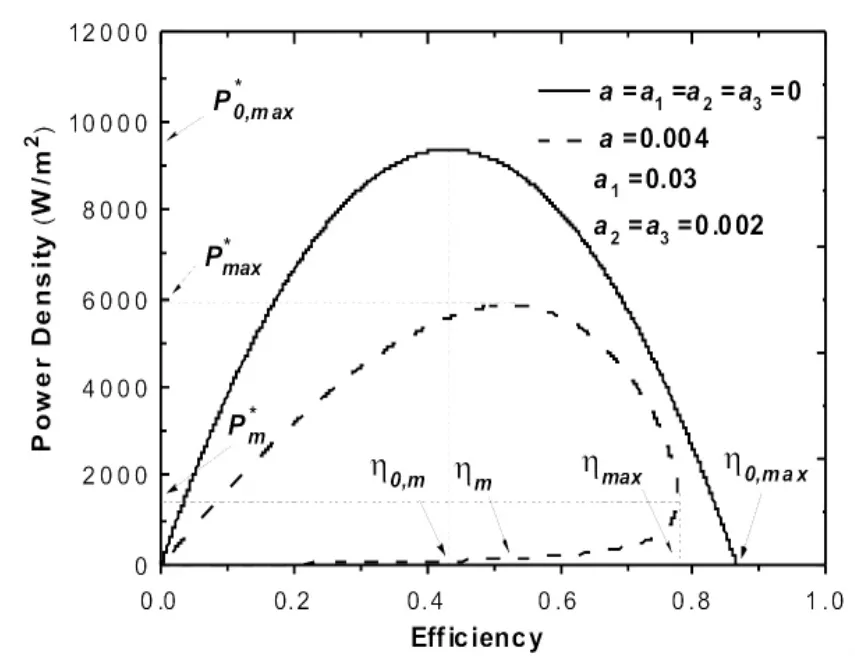
图10 在不同参数 a,a1,a2,a3和下功率密度随效率变化的曲线

4 结论

本文的重点在于建立了一个新循环模型，该模型可以描述MCFC-斯特林热机耦合系统的一般特性。描述了不可逆的热力学和电化学损失，并且通过参数分析方法研究了耦合系统这些不可逆性的个体效应。分析研究发现通过使用斯特林热机进一步发电，MCFC的性能可以得到显著地增强。整个系统通过数值模拟确定了效率和输出功率的上限与下限。此外，还讨论了一些工作条件比如工作温度、阳极和阴极的气体分压以及工作压力对耦合系统性能的影响。详细讨论如何考虑在电流密度最佳范围内的效率和输出功率这个问题。获得的结果可能会为MCFC-斯特林热机耦合系统的优化设计和操作实际提供一些理论基础。这种方法可以很容易地扩展到其它的燃料电池耦合系统开发。

参考文献：

［1］HEINZ B，HENKEL J．Balancing wind energy and participating in electricity markets with a fuel cell population［J］．Energy，2012，48：188-195．

［2］NEEF H J．International overview of hydrogen and fuel cell research［J］．Energy，2009，34：327-333．

［3］FENG L，CAI W，LI C，et al．Fabrication and performance evaluation for a novel small planar passive direct methanol fuel cell stack［J］．Fuel，2012，94：401-408．

［4］VERDA V，SCIACOVELLI A．Optimal design and operation of a biogas fuelled MCFC（molten carbonate fuel cells）system integrated with an anaerobic digester［J］．Energy，2012，47：150-157．

［5］ZHANG H，LIN G，CHEN J．Performance evaluation and parametric optimum criteria of an irreversible molten carbonate fuel cell-heat engine hybrid system［J］．Int J Electrochem Sci，2011（6）：4714-4729．

［6］ZHANG H，SU S，LIN G，et al．Performance analysis and multi-objective optimization of a molten carbonate fuel cell-Braysson heat engine hybrid system［J］．Int J Electrochem Sci，2012（7）：3420-3435．

［7］BROUWER J，JABBARI F，LEAL E M，et al Analysis of a molten carbonate fuel cell：numerical modeling and experimental validation［J］．J Power Sources，2006，158：213-224．

［8］KIM H，BAE J，CHOI D．An analysis for a molten carbonate fuel cell of complex geometry using three-dimensional transport equations with electrochemical reactions［J］．Int J Hydrogen Energy 2013，38：4782-4791．

［9］ZHANG H，LIN G，CHEN J．Performance analysis and multi-objective optimization of a new molten carbonate fuel cell system［J］．Int J Hydrogen Energy，2011，36：4015-4021．

［10］CHEN J，YAN Z，CHEN L，et al．Efficiency bound of a solar-driven Stirling heat engine system[J]．Int J Energy Res，1998，22：805-812．

［11］ZEMANSKY M W．Heat and thermodynamics［M］．5th ed．New York：McGraw-Hill，1968．

［12］ZHAO Y，CHEN J．Modeling and optimization of a typical fuel cell-heat engine hybrid system and its parametric design criteria［J］．J Power Sources，2009，186：96-103．

［13］ZHANG X，GUO J，CHEN J．Influence of multiple irreversible losses on the performance of a molten carbonate fuel cell-gas turbine hybrid system［J］．Int J Hydrogen Energy，2012，37：64-71．

［14］NICOLIN F，VERDA V．Lifetime optimization of a molten carbonate fuel cell power system coupled with hydrogen production［J］．Energy，2011，36：35-41．

［15］PAPADIAS DD，AHMED S，KUMAR R．Fuel quality issues with biogas energy-An economic analysis for a stationary fuel cell system［J］．Energy，2012，44：257-277．

［16］VERDA V，NICOLIN F．Thermodynamic and economic optimization of a MCFC-based hybrid system for the combined production of electricity and hydrogen［J］．Int J Hydrogen Energy，2010，35：794-806．

［17］DESIDERI U，PROIETTI S，SDRINGOLA P，et al．MCFC-based CO2capture system for small scale CHP plants ［J］.Int J Hydrogen Energy，2012，37：19295-19303．

［18］MASOUD R．Thermodynamic analysis of SOFC （solid oxide fuel cell）-Stirling hybrid plants using alternative fuels ［EB／OL］．Energy，2013，http：dx．doi．org／10．1016／j．energy．2013．06．001．

［19］RO S T，SOHN J L．Some issues on performance analysis of fuel cells in thermodynamic point of view[J]．J Power Sources，2007，167：295-301．

［20］ZHAO Y，OU C，CHEN J．A new analytical approach to model and evaluate the performance of a class of irreversible fuel cells［J］．Int J Hydrogen Energy，2008，33：4161-4170．

［21］YUH C Y，SELMAN J R．The polarization of molten carbonate fuel cell electrodes I:analysis of steady-state polarization data［J］．J Electrochem Soc，1991，138：3642-3648．

［22］HITCHINGS C．Fuel cell handbook［M］．6th ed．Virginia：EG＆G Technical Services Inc，2002．

［23］ZEMANSKY M W．Heat and thermodynamics［M］．5th ed．New York：McGraw-Hill，1968．

［24］AyRES R U，MCKENNA R P．Alternatives to the internal combustion engines[M]．Baltimore M D：The Johns Hopkins University Press，1972．

［25］BAVARSAD P G．Energy and exergy analysis of internal reforming solid oxide fuel cell–gas turbine hybrid system[J]．Int J Hydrogen Energy，2007，32：4591-4599．

［26］QUDDUS M R，ZHANG Y，RAY A K．Multi-objective optimization in solid oxide fuel cell for oxidative coupling of methane［J］．Chem Eng J，2010，165：639-648．

［27］AUTISSIER N，PALAZZI F，MARECHAL F，et al.Thermo-economic optimization of a solid oxide fuel cell，gas turbine hybrid system［J］．J Fuel Cell Sci Technol，2007（4）：123-1299．

［28］ANG SMC，BRETT D J L，FRAGA E S．A multi-objective optimization model for a general polymer electrolyte membrane fuel cell system［J］．J Power Sources，2010，195：2754-2763．

(责任编辑：朱联九）

Performance Optimum Analysis of a Molten Carbonate Fuel Cell-Stirling Heat Engine Hybrid System

CHEN Li-wei

(School of Mechanical and Electrical Engineering,Sanming University,Sanming 365004,China)

A new hybrid system mainly consists of a molten carbonate fuel cell(MCFC)and a Stirling heat engine is established,where the Stirling heat engine is driven by the high-quality waste heat generated in the MCFC.Based on the electrochemistry and non-equilibrium thermodynamics,analytical expressions for the efficiency and power output of the hybrid system are derived by taking various irreversible losses into account.It is showed that the performance of the MCFC can be greatly enhanced by coupling a Stirling heat engine to further convert the waste heat for power generation.By employing numerical calculations,not only the influences of multiple irreversible losses on the performance of the hybrid system are analyzed,but also the impacts of some operating conditions such as the operating temperature,input gas compositions and operating pressure on the performance of the hybrid system are also discussed.

molten carbonate fuel cell;Stirling heat engine;hybrid system;performance optimum analysis

TM911．4

A

1673-4343（2014）04-0045-09

10．14098／j．cn35－1288／z．2014．04．009

2014-06-08

福建省教育厅科技项目（JA13291）

陈礼炜，女，福建永安人，讲师，博士。研究方向：工程热力学、清洁能源利用。