基于混合算法的汽车零部件物流配送路径优化

侯秀英，李正红，林 森，罗奕辉，邹 斌

（福建农林大学 交通与土木工程学院,福建 福州 350002）

基于混合算法的汽车零部件物流配送路径优化

侯秀英，李正红，林 森，罗奕辉，邹 斌

（福建农林大学 交通与土木工程学院,福建 福州 350002）

针对汽车零部件供应物流，建立循环取货配送路径优化模型，将遗传算法与Max-Min蚁群算法融合，采用遗传算法生成初始信息素分布，利用Max-Min蚁群算法求精确解，并通过实例验证。结果表明，混合算法对于解决供应商数量多、带时间窗限制与碳排放限制的配送路径优化问题，可有效降低车辆取货频次和提高车辆装载率。

汽车零部件；循环取货；遗传算法；Max-Min蚁群算法

汽车制造企业增强供应链竞争能力的重要环节之一就是汽车零部件物流。汽车零部件数量多，因此供应商数量多，导致零部件供应物流的组织与运行成为汽车物流中难度最重要和最复杂的环节之一[1]，对供应链的敏捷度、企业的物流成本等方面的影响日益凸显。为更好的运用运输车辆，降低物流成本，提高供应链敏捷度，循环取货成为许多汽车制造企业供应物流模式的首选，并在一些国际著名汽车制造企业中得到成功的应用。

对于汽车循环取货而言，由于供应商数量多与严格的时间窗口限制，会导致车辆装载率下降、取货成本上升等问题，因此零部件物流车辆路径问题（即VRP）是关键，即如何合理安排车辆从配送中心对顾客进行配给货物使总运距离最短。本文以国内一家著名的汽车物流企业实际情况为背景，对其零部件循环取货的车辆路线问题进行优化设计，建立相应的数学模型，并将遗传算法与Max-Min蚁群算法融合进行优化求解。

1 循环取货路径规划模型

汽车零件部件供需系统通常由若干个供应商、若干台运输车辆和一个零部件配送中心构成[2]，采用循环取货模式时，要在既定的约束条件下合理安排运输车辆的行车路线，使得用最少车辆进行配送。目前大多数研究就是追求路径最短及单次取货量最大，从而达到降低运输成本的目的，但对由于物流系统中存在的效益悖反现象所造成的供应商库存成本升高等其他问题则表现为忽略的态度，导致难以实现整个系统最优化。在配送过程中，如何实现绿色运输也是需要考虑的问题。未来物流要做到可持续发展，必须走低碳化道路，运输过程中应尽量控制碳排放，将碳排放作为取货路径设计考虑的因素之一。因此，针对带时间窗的循环取货问题，在建立模型时以尽量降低运输成本和供应商的库存成本为目标，并以控制碳排放量作为约束条件，使得汽车零部件物流配送既获得较好的经济效益，又实现物流的绿色化。

假设有n个供应商点，有m条配送路径，循环取货VRP模型如下：

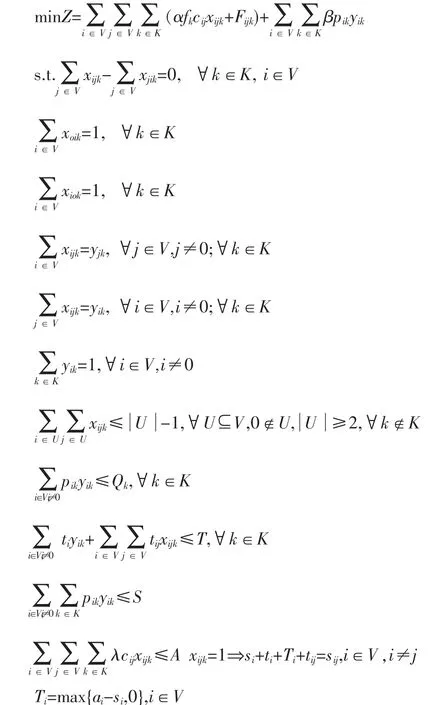
其中，V={i|i=0,1,2,…，n}为n个供应商点与主机厂的集合，i=0代表主机厂；K={k|k=0,1,2,…，m}为m条路径集合；fk为路径的取货频次；Cij为供应商i到j的距离，特别地Cii=0；Pik表示如果路径k经过供应商i，则一个车次到i处的单次取货量为Pik=(di/fk)；di为供应商i的全天需求量；Qk为路径k上车的容量限制；ti为供应商i的装卸货时间k；tij为供应商i到j的行驶时间；T为每条路径单次循环时间的最大允许值；S为制造企业允许的最高库存量；α为单位距离运输成本；β为零部件的在主机厂的单位库存成本；Fijk为第k条路径上的固定成本；Si为车辆到达供应商i处的时刻；Ti为车辆在供应商i处的等待时间；ai为供应商在i处允许最早接受服务时间；bi为供应商i处允许最迟接受服务时间；λ为单位距离的平均碳排放量；A为每次取货允许的最大碳排放量。

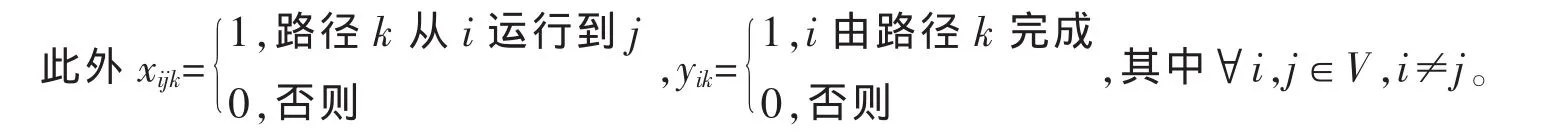
2 模型求解的混合算法

2.1遗传与Max-Min蚁群混合算法

对于VRP问题的求解，目前一些文献常采用某一种智能算法进行求解，但每种算法都存在一定的问题，如蚁群算法，其前期搜索的局限性、算法收敛性都比较差，导致求解结果不够精确，因此考虑两种算法混合求解。本文将遗传算法与Max-Min蚁群算法进行融合，汲取两种算法的优点，克服各自的缺陷，优势互补，使得混合算法在时间效率上优于蚁群算法，在求精解效率上优于遗传算法。混合算法的基本思想是算法前过程采用遗传算法，充分利用遗传算法的快速性、随机性、全局收敛性，其结果是产生有关问题的初始信息素分布[3]；算法后过程采用Max-Min蚁群算法，在有一定初始信息素分布的情况下，充分利用蚁群算法并行性、正反馈性、求精解效率高等特点，实现两种算法的优势互补。

2.1.1 遗传算法初代种群初始化

为了避免遗传算法在初期盲目性的搜索，我们先对初代种群进行如下初始化，即把供应商的点作为染色体（这里采用符号编码），随机选择一个点，然后判断该点是否满足碳排放、载重量和时间窗，若是满足，则加入到该染色体中，否则选择一个点，直至所有点都被选择过。

2.1.2 轮盘赌选择方法

轮盘赌选择的基本思想是各个个体被选中的概率与其适应度函数值大小成正比。设群体大小为N，个体xi的适应度为f(xi)，这里的适应度函数取目标函数，则个体xi的选择概率为：

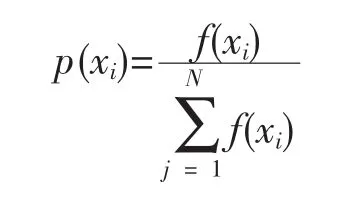
2.1.3 个体保优策略

通过遗传算法对个体的交叉与变异等操作，可以不断更新出优良的新生个体。但由于本身的遗传操作是基于随机性的，故有时会破坏目前最好的适应度值，从而造成整体的种群平均适应值下降。为此提出了个体保优策略来进行优胜劣汰操作，即当前群体中适应度最好的个体不参与交叉、变异遗传操作，而是用它来替换本代群体中经过交叉、变异操作后所产生的适应度值最低的个体[3]。

2.1.4 次序交叉

为了能够更好的贴近自然界进化规律，选择次序交叉作为该遗传算法中的交叉操作，从而随机性生成新个体。次序交叉指的是首先，对随机的两个新种群，找到两个交叉点，将交叉点之间的数值移动到最后面，得到临时两个种群；然后，交换原先新种群交叉之间的数值；最后，已交叉后的新种群为依据，将临时种群依次填补两个交叉点前后的空值，在此期间要保证数值不能有重复。

2.1.5 替换变异

作为遗传算法另外一个重要的遗传操作变异，其可以产生种群未曾出现过的新生代。虽然变异操作只是产生新个体的辅助方法，但它也是必不可少的一种遗传操作，因为它决定了遗传算法的局部搜索能力。交叉与变异的相互配合，共同完成对搜索空间的全局搜索和局部搜索，从而使得遗传算法能够以良好的搜索性能完成最优化问题的寻优过程[4]。

替换变异指的是首先在种群中随机找到两个变异点x1，x2，暂时移除两个变异点之间的数值。然后，在剩下的染色体字段中随机到一点rnd，将变异点之间的数值插入rnd中。最后根据变异种群是否满足相应的约束条件来判断种群变异失败与否。

2.1.6 蚂蚁信息素初始化

MMAS是把各路径信息素初值设为

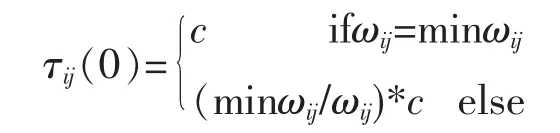
通过遗传算法得到了一定的路径信息素，把信息素的初值设置为

其中c为常量，f(xij)是该条路径上的目标函数值。

2.1.7 改善信息素更新

为尽可能的避免早熟（局部最优）和提高解的质量，在算法的运行中期，引入趋于相同路径的蚂蚁数γ和负反馈因子δ，对信息素的全局更新进行动态调节来改善探索新路径的能力，从而达到进一步提高求解质量的目的[5]。采用的公式如式（2）～（5）：

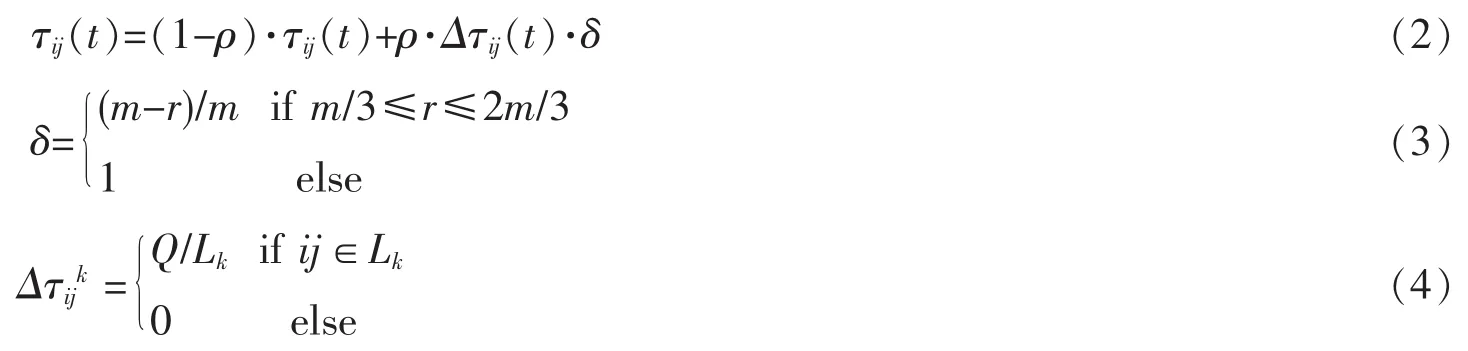
式（4）中Q是一个常数，在这里取1；Lk表示在本次循环中第k只蚂蚁所走过路径的长度。

2.1.8 改善蚂蚁的能见度

为了弥补运行后期时，即当所有蚂蚁中有h只蚂蚁所走路径完全相同时，可能会遗漏更优节点的选择，引入适当增大能见度机制，从而改善蚂蚁路径选择的影响力，进一步提高解的质量[5]。公式如式（5）～（6）：

2.1.9 蚂蚁转移概率选择

借鉴Dorigo等的Ant-Q算法思想，采用确定性与随机选择策略，根据式(4)和式(5)结合节约算法对蚁群算法转移规则进行细化[6]，定义如下形式的蚂蚁转移概率：

《城市绿化条例》与《风景名胜区条例》是风景园林行业主要的行政法规，它们对我国绿化事业的发展，改善、美化生态与生活环境，充分保护风景名胜资源，有效进行行业管理等方面做出了明确的约束和规定。

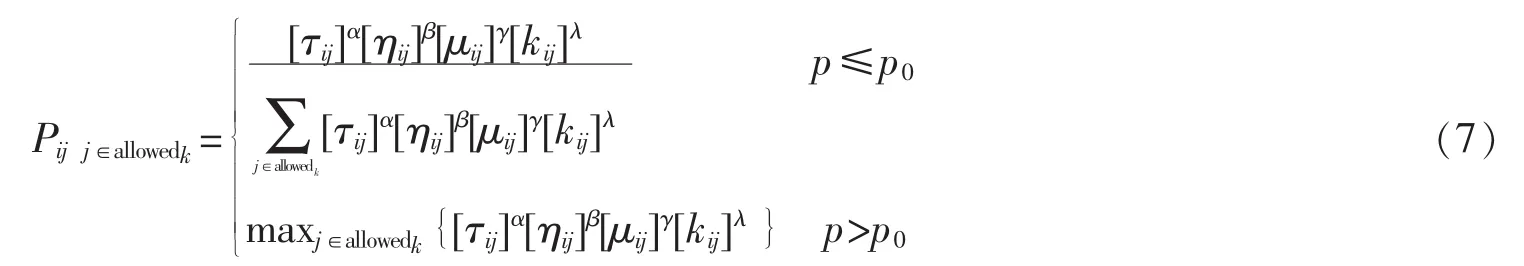
式(7)中：τij为边(i,j)上的信息素；ηij为边(i,j)上的启发信息，值为边(i,j)长度的倒数，即ηij=1/dij；μij表示将点i与j在满足车辆容量约束的基础上连接在j一条线路上的费用节约值，其值通过节约算法求得，先将各点单独与源点0相连，构成1条已含一个点的线路，然后计算μij=dio+doj-dij，μij越大，收益越大，选择结点μj的概率也就越大，但μij的值需要作最大值和最小值限制，以免μij过大或过小而影响整个路径转移概率。在这里做如下的规定：当μij≤0，取μij=0.01；当μij≥10时，取μij=10，这样的话就可以使得整个转移概率公式的其他影响因素失去意义；kij=(qi+qj)/Q是考虑车辆容量约束和车辆容量利用率而引入的变量；α、β、γ、λ为权重参数；p是取值在(0,1)区间内的随机数；p0取0.1。

2.2 算法步骤

混合算法求解VRP问题步骤如下。

步骤1：初始化．初始化蚂蚁数n，供应商数量m，单位距离运输成本unitCost，信息素挥发参数ρ，影响因子α、β、γ、λ，固定成本cost，每条路径上单次循环时间的最大值maxTime，单位距离的碳排放量carbon、每次循环取货允许的最大碳排放量maxCarbonEmission及信息素轨迹范围[τmin,τmax]；

步骤2：初始化遗传算法的种群个数ind_N、交叉率p_c_t、变异率p_m_t。

步骤3：初始化初代种群的分布，该分布满足碳排放、载重量、时间窗。

步骤4：进化次数是否已经达到了MAX_GEN，如果已经达到，则跳转到步骤9；否则跳转到步骤5。

步骤5：比例选择，这里利用在[0,1]之间随机数来确定被选中的下一代种群初始染色体，以及被选中的次数。

步骤7：随机选择两个种群，进行次序交叉。判断交叉后的种群是否满足载重量、碳排放、时间窗，如果满足则跳转到步骤8，否则判断当前次数是否小于m，如果小于，则进入下一循环，同时种群回退到上一代的染色体状态。否则跳转到步骤6，同时种群回退到上一代的染色体状态。

步骤8：对次序交叉后的种群进行替换变异，判断变异后的种群染色体是否满足载重量、碳排放、时间窗。如果不满足，则种群回退到交叉遗传操作之前的染色体状态，否则保存该新生种群的染色体。跳转步骤到6。

步骤9：初始化信息素．根据给定数据，按式(1)计算各边初始信息素轨迹最；

步骤10：构造解，初始化最大迭代次数MAX_GEN。每只蚂蚁的初始出发位置都为配送中心，根据(5)(6)(7)式选择下一个供应商地点。如果该点满足以每一条路径上车辆载重量总和小于最大的车辆载重量、每一条路径上碳排放量总和小于允许的最大碳排放量以及每一条路径上所花的时间也小于允许的时间，则将该点置于该蚂蚁的禁忌表中，并从allowed表中删除该点，直到该蚂蚁(车)均不满足上述的3个条件，则返回至配送中心。重复循环直到所有供应商地点都被访问过，计算目标函数值，记录下当前最好的路径长度以及其对应tabu中的点[6]。

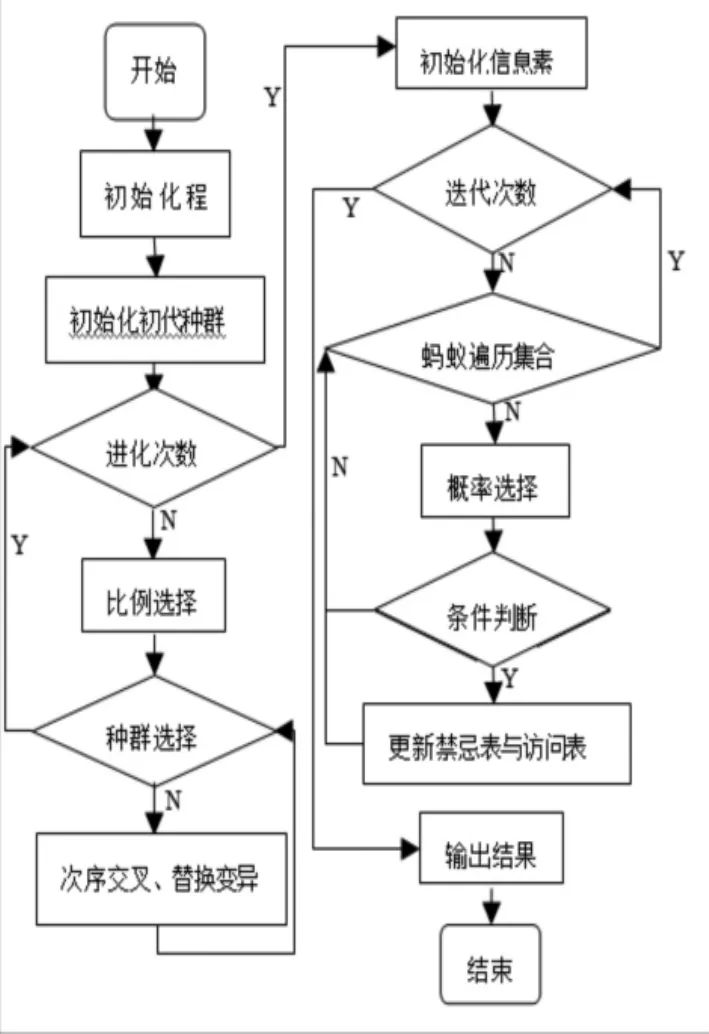
图1 算法流程图

步骤11：重复步骤10，直到所有蚂蚁都构造好相应的解

步骤12：比较所有蚂蚁的路径，累计h及r，更新最小目标函数值的路径及路径条数，根据式(2)(3) (4)更新各边信息素轨迹，并根据Max-Min思想限制信息素轨迹量[6]；

步骤13：迭代次数依次递增；

步骤14：若迭代次数超过MAX_GEN或蚁群全部收敛到相同路径，则输出最优解，否则转步骤10。

算法流程图见图1。

2.3 参数设计

计算中，一些参数的选取会对算法的的运行速度与最优解等产生重要影响，以下对交叉率p_c_t、变异率p_m_t与信息素挥发参数ρ 3个参数进行设计。

在进行初始化时，交叉率与变异率的取值尤为重要。交叉率p_c_t决定了种群的多样性，而变异率p_m_t则决定了程序跳出局部最优解的能力。在运行过程中发现，交叉率和变异率的取值不能太大，如果交叉率太大会使种群的多样性变小，而变异率太大则会频繁破坏种群。因此，经过分析，选取3组参数进行计算，运行结果见表1，由表1可见，选取第2组参数可获得更优结果。

信息素挥发参数ρ决定蚂蚁是否能够找寻到原有的路线。ρ取值过大会造成信息素挥发过快，导致不能利用之前所得到结果值，而取值过低则会导致陷入局部最优，影响整体最优的求解。其它参数不变，分别选取信息素挥发参数ρ为0.1、0.5和1.0 3组计算，运行结果见表2，由表2可知，选取第2组的ρ=0.5可获得更优结果。

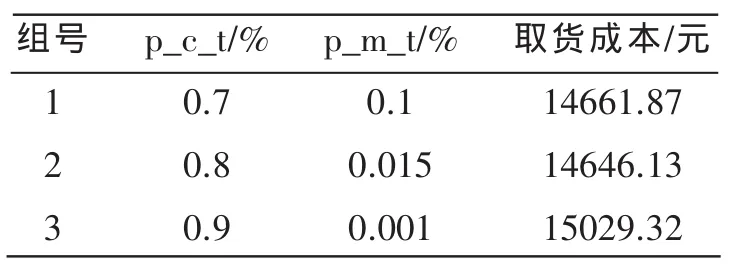
表1 选取的3组交叉率与变异率数值及运行结果

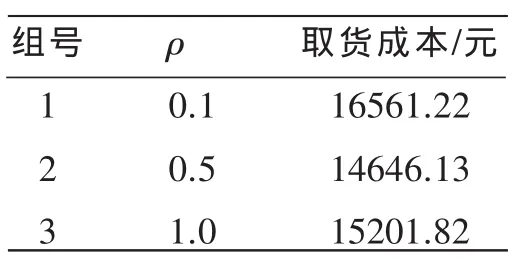
表2 选取不同ρ值及运行结果

3 实例验证

某物流企业目前为上海大众、上海通用、上汽通用五菱、一汽丰田、广汽丰田、比亚迪等多家国内主机厂提供物流服务，其零部件入厂物流业务采用循环取货方式，目前运输成本较高，车辆装载率低于85%，装载率低。该物流企业目前在上海有一家主机厂，200家循环取货的供应商，主要分布在上海和江苏，由于供应商数量众多，配送量差异较大，因此先对供应商进行层次聚类分析和概率选择。在概率选择中，由于所有供应商提供的供应量数据离散性较强，而且实际上每家供应商提供的量也是差异化的，选出的所有供应商满足离散型概率的程度高于连续型概率。借鉴乘客坐公交车概率问题，提出了每个供应商取货量的概率，公式见式(8)。

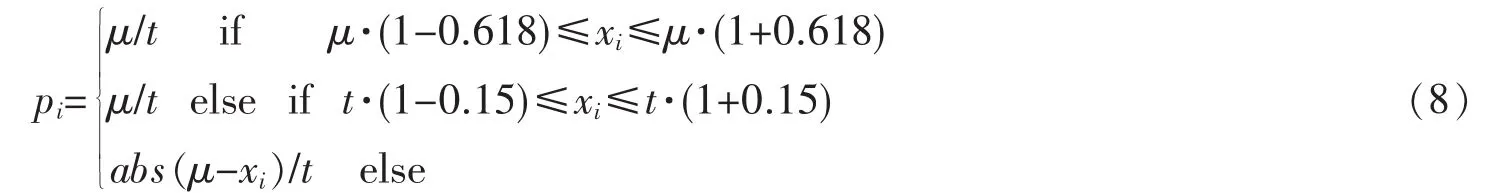
根据上述计算，符合降低取货频次的原则，选择出41家供应商作为研究对象。配送中心的坐标是（31.2961，121.1702），15台运输车辆对41家供应商进行循环取货，载重量5吨，车辆容积12×2.3× 2.3 m3，取货量用货物体积表示。计算过程中，根据美国加州环保机构的数据，我国运输车辆C02平均排放量约为190～200 g/km[7]，而运输货车载货量较大碳排放量更高，因此，结合相关标准，根据载货量的平均值设定运输车辆单位距离的碳排放量为203 g/km，并确定每次取货允许的最大排放量为82000 g。此外，每条路径单次循环时间最大允许值为6 h，种群交叉率取0.8%，种群变异率取0.015%，信息素挥发参数取0.5，残留信息素的重要程度取2.0，启发信息的重要程度取2.5，费用节约值的重要程度取1.0，车辆容量约束和车辆容量利用率的权重参数值取1.0。采用MATLAB软件进行运算，运行50次后，得到的最优结果见表3。

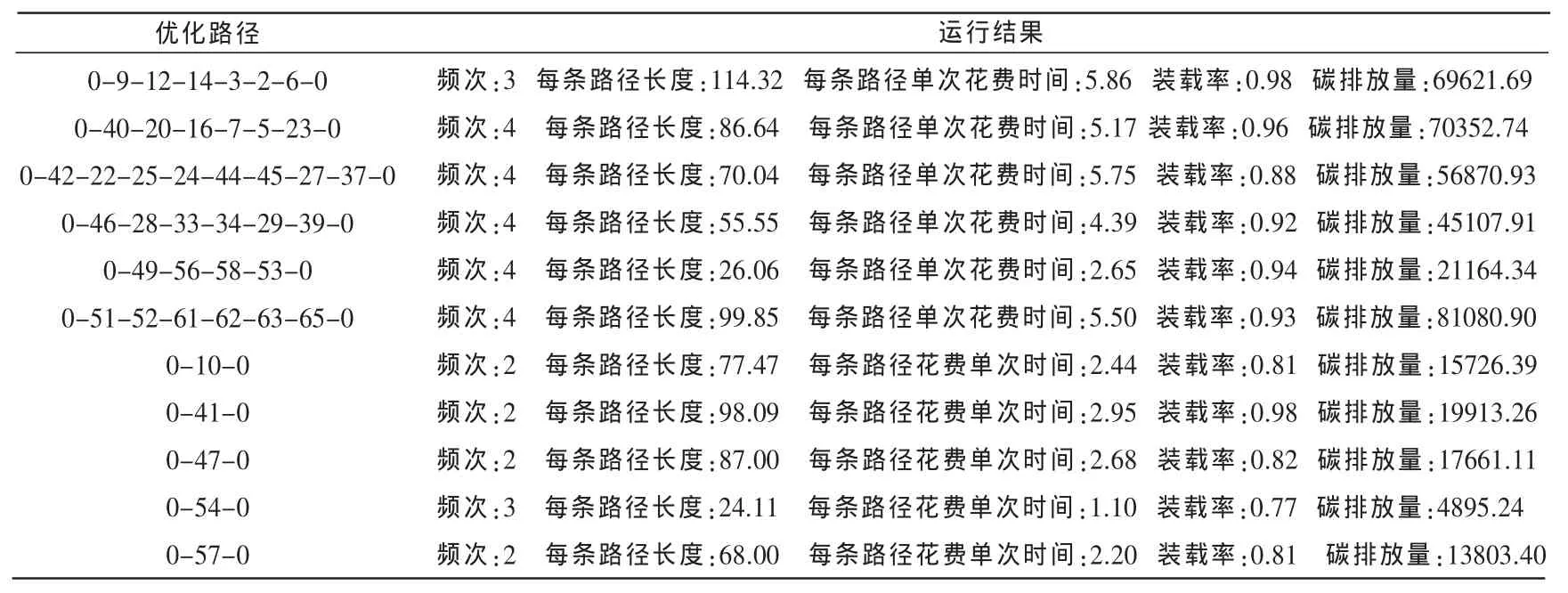
表3 运行50次的计算结果

由上述结算结果可以知道，41家供应商通过11条线路进行取货，80%的单点取货频次为2次，20%的单点配送频次为3次，基本能达到降低频次的目的；而在装载容积上，多点取货车辆装载率最低88%，83.3%线路车辆装载率超过90%；单点取货车辆装载率相对较低，最低77%，80%线路车辆装载率超过80%，最高可达98%，接近满载，基本解决企业原来存在的车辆装载容积率低的问题。此外，每条线路的碳排放量都少于每次取货允许最大排放量。

将采用混合算法与采用遗传算法、Max-Min蚁群算法进行比较，结果见表4，由表4可见，采用混合算法运行的结果更加优化，且运行速度快。

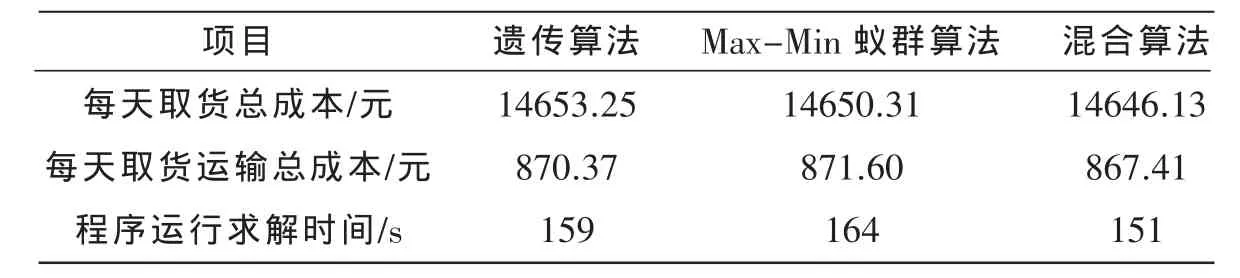
表4 几种算法运行结果比较

4 结束语

将混合算法用于求解汽车零部件供应物流中的VRP问题，所得结果比单独采用遗传算法或Max-Min蚁群算法更加合理，在提高车辆装载率方面有显著作用，并能有效减少车辆取货频次，使碳排放量控制在标准范围之内，降低取货成本。因此，将遗传算法与Max-Min蚁群算法混合求解供应商数量多、带时间窗限制与碳排放限制的汽车零部件供应物流配送路径问题可得到较优结果。

［1］左晓露，刘志学．汽车零部件循环取货物流模式的分析的分析与优化［J］．汽车工程，2011，33（1）：79-84．

［2］郎茂祥．基于遗传算法的物流配送路径优化问题研究［J］．中国公路学报，2002，15（3）：76-79．

［3］苏涛，韩庆田．VRP问题蚁群算法研究［J］．计算机与现代化，2012（11）：1006-2475．

［4］丁建立，陈增强．遗传算法与蚂蚁算法的融合［J］．计算机研究与发展，2003，40（9）：1352-1353．

［5］陈国良，王煦法．遗传算法原理及应用［M］．北京：人民邮电出版社，1996．

［6］王更生，俞云新．一种改进蚁群算法求解VRP问题［C］//南昌：信息技术与应用学术会议论文集，2009：255-256．

［7］车昱．基于绿色供应链的循环取货模式研究［D］．北京：北京交通大学，2012．

（责任编辑：朱联九）

Optimization of Auto Parts Logistics Distribution Path Based on Hybrid Algorithm

HOU Xiu-ying,LI Zheng-hong,LIN Sen,LUO Yi-hui,ZOU Bin

(College of Transportation and Civil Engineering,Fujian Agriculture and Forestry University,Fuzhou 350002,China))

According to the supply logistics of automobile parts,milk-run distribution path optimization model is established.The Max-Min genetic algorithm and ant colony algorithm are fused.Genetic algorithm is adopted to give information pheromone distribution;the ant algorithm is used to give the precision of the solution,and is verified by an example.The results show that the hybrid algorithm can effectively reduce the distribute frequency and improve vehicle loading rate for solving the distribution path problem of supplier and limiting the time window and carbon emissions.

auto parts；milkrun；genetic algorithm；Max-Min ant colony algorithm

F224

A

1673-4343（2014）04-0038-07

10．14098／j．cn35－1288／z．2014．04．008

2014-06-08

福建农林大学科技创新（培育）团队资助计划（pytd12006）。

侯秀英，女，福建永泰人，副教授。研究方向：物流技术与管理。通讯作者：李正红，女，福建浦城人，教授。研究方向：物流技术与管理。