阵列误差对智能天线算法性能影响的分析与研究
2014-02-23吴美瑜刘持标
吴美瑜,刘持标
(三明学院 信息工程学院 物联网应用福建省高校工程研究中心,福建 三明 365004)
阵列误差对智能天线算法性能影响的分析与研究
吴美瑜,刘持标
(三明学院 信息工程学院 物联网应用福建省高校工程研究中心,福建 三明 365004)
采用智能天线技术可提高物联网的系统容量以及无线通信系统的频谱利用率。通过建立阵列幅相误差模型,针对ESB算法进行稳健性分析,探讨阵列幅相误差情况对算法性能的影响,并给出MATLAB仿真分析图。实验结果表明,阵列幅相误差会使得实际阵列方向矢量不再是理想条件下的阵列方向矢量,进而严重影响了智能天线系统的性能。
智能天线;幅相误差;性能影响;ESB算法
智能天线技术通过引入空分多址技术(SDMA),可提高物联网的系统容量以及无线通信系统的频谱利用率。智能天线是一种阵列天线,它通过改变各阵元信号的加权幅度和相位来调整阵列的方向图形状[1]。即可以自适应或以预制方式控制波束的指向、幅度和零点位置,使主波束总是指向期望方向,而零陷指向干扰方向[2]。这样就实现了波束跟随着期望方向走,进而提高天线的信干噪比和增益,节省发射功率,降低硬件设备体积等[3]。
智能天线性能的优劣主要取决于波束形成算法性能的优劣。经典波束形成算法基本都是在理想环境下才具有良好的性能[4]。然而,在实际应用中的通信环境和天线系统是不可能符合理想情况的,通常情况下都会存在各种误差,比如通道幅相误差、指向误差、阵元位置误差、导向向量误差、协方差矩阵误差等,而且多个信号源信号可能相关,噪声信号可能并不是常见的高斯白噪声等等[5-9]。ESB(特征空间)算法完全舍弃噪声子空间,只保留了信号子空间的分量。这样权矢量的范数变小,输出噪声功率也变小,期望信号和干扰信号的输出功率不变,所以输出的信干噪比(SINR)较大,有利于波束保形[10]。本文将通过建立阵列误差模型,针对ESB算法进行稳健性分析,探讨不同阵列误差情况对算法性能的影响,并给出MATLAB仿真分析图。
1 阵列模型
由于均匀线阵结构简单、处理方便,是应用得最为广泛的天线阵列形式,所以本文采用均匀线阵来进行自适应波束形成算法的稳健性的分析。假设本文所研究的信号是窄带远场信号;噪声为空间理想的白噪声,且相互独立、方差为零;阵元间隔λ/2。假设用s(k)表示基带复包络的调制波形,θi为信号的入射方向,设i=0时为期望信号,i=1,2,...,N时为干扰信号,阵元个数为M。则阵列接收信号可以表示为:

其中x(k)是M×1维的阵列快拍数据矢量,s(k)是N×1维的阵列信号数据矢量,ν(k)是M×1维的阵列噪声数据矢量,A=[a0(w0),a1(w0),...,aN(w0)]为维M×N的阵列流型矩阵,ai(w0)是阵列导向矢量。其中,导向矢量:
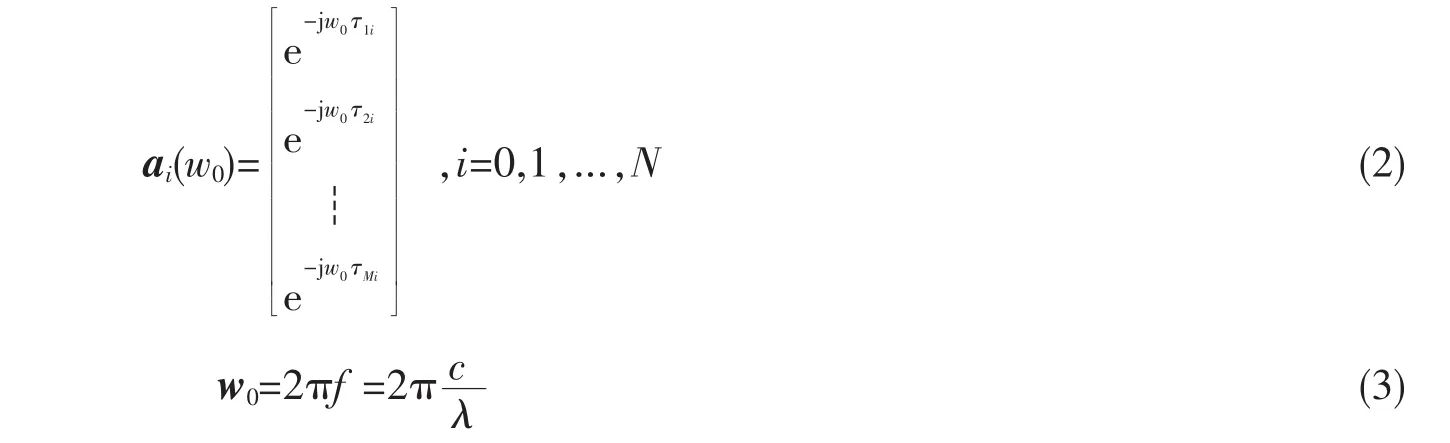
式(3)中,c是波在空间中的传播速度,λ是入射信源的波长。
根据MSNR准则的最佳权矢量为:
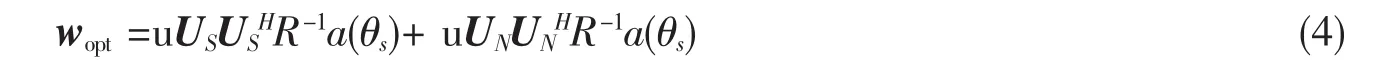
在理想情况下,因为a(θs)在信号子空间,所以uUNUNHR-1a(θs)=0。但是在实际实现时采用有限样本来估计R,因而不等于0并将使处理器的性能降低。ESB算法针对此问题,摒弃权矢量在噪声子空间中的分量而仅保留在信号子空间的分量并取最佳权矢量为[11]为

这样权矢量的范数变小,输出噪声功率也变小,期望信号和干扰信号的输出功率不变,所以输出的信干噪比(SINR)较大,有利于波束保形[10]。
ESB算法是基于上述理想的数学理论模型,但当阵列通道不理想时,算法的性能也将受到影响。为了算法仍能够有效工作,则要校正阵列误差,提高算法的稳健性。阵列误差大致可分为如下两大类:阵元位置误差和波束指向误差是与方位相关的,故可称之为方位依赖误差;反之,阵列通道幅相误差和阵元互耦效应则是与方位无关的方位独立误差。方位依赖误差,顾名思义,会随着空间方位的变化而变化,其校正也就失去了意义,且可以通过提高天线的制作工艺水平使得阵元误差可以忽略不计;而阵元互耦效应又要用到互耦及网络端口模型等理论,所以至今也还没有合理的解决方案;通道幅相误差是最常见的阵列误差之,其解决方法也较多[3-6]。因此本文主要研究分析窄带下的通道幅相误差对ESB算法的影响。
由于阵元通道幅相误差与信源方位无关,可用Г表示复数幅相误差矢量,则存在通道幅相误差的信号模型可以表示为:

式(6)中,复数幅相误差矢量Г=diag[ρ1exp(φ1),ρ2exp(φ2),...,ρMexp(φM)],diag代表对角阵,ρm(1≤m≤M)为第m个阵元通道的幅度误差,φm为第m个阵元通道的相位误差。不失一般性地,第一个阵元通道通常被当作增益和相位的基准,则ρ1=1,φ1=0。
2 仿真实验分析
为分析阵列通道幅相误差对算法性能的影响,用MATLAB软件进行仿真。假设采用16阵元均匀线阵,阵元间距为λ/2。设有3个信号源入射,有用信号到达角为0°,干扰信号到达角分别为-30° 和20°,且有用信号和干扰信号之间不相关。信噪比SNR为20 dB,INR为20 dB。阵元噪声为与信源不相关的空间白噪声。
实验1:当只存在幅度误差时,幅度误差是上下界为±0.4(单位为1)的随机值。图1是当阵列通道无误差时,用经典的高分辨率子空间算法MUSIC算法能够近乎准确地估计出DOA,且空间谱谱峰尖锐。此时ESB波束赋形良好,主瓣波束增益比旁瓣波束增益至少高12 dB左右,并且在干扰方向-30°和20°处形成较深的零陷,实现了在有用信号方向形成高增益波束而在干扰方位形成零陷以抑制干扰的目的。
当阵列通道存在幅度误差时,图1说明:存在通道幅度误差的波束主瓣与无误差时的波束主瓣基本一致,但是在两个干扰方位却并未形成零陷,且旁瓣电平抬高不少。由图2可知:这时DOA估计的角度仍然较为准确,只是空间谱的谱峰比较平缓。可以看出,当阵列通道中只存在幅度误差时,波束主瓣的影响很小,主要是对旁瓣和干扰零陷的影响较大。

图1 幅度误差情况下的波束图

图2 幅度误差情况下的DOA估计
实验2:当只存在相位误差时,相位误差是在(-25°,25°)内的随机值。图3是当阵列通道是否存在相位误差情况下的波束图,图4是当阵列通道是否存在相位误差情况下的DOA估计功率谱图。
由图3可知:主瓣稍微偏移,旁瓣电平大幅度抬高,干扰方位没有形成零陷。由图4又可看出:在阵列通道存在相位误差时,DOA估计偏差比较明显,而且谱峰非常平缓。可以看出,当阵列通道中只存在相位误差时,不仅对旁瓣和干扰零陷的影响较大,而且还会造成波束主瓣的偏移。
实验3:当存在幅相误差时,幅度误差是上下界为±0.4(单位为1)的随机值,而相位误差是在(-25°,25°)内的随机值。
从图5可以看出,当阵列通道存在幅相误差时,主瓣向右偏移较大,旁瓣电平大幅度抬高,干扰方位没有形成零陷。图6说明此时DOA估计偏差较大,空间谱谱峰不明显。
从图1~6中可以看出,当阵列通道中既存在幅度误差又存在相位误差时,波束图的性能下降更为严重。
3 结束语
对于ESB自适应波束形成,实验结果表明:阵列幅相误差会使得实际阵列方向矢量不再是理想条件下的阵列方向矢量,进而严重影响了阵列天线系统的性能。幅度误差仅会抬高实际波束图的旁瓣电平和降低DOA估计的谱峰值,对DOA估计的准确性几乎没有影响;但相位误差则不但抬高了旁瓣电平,且波束指向出现相应偏移,干扰位置偏移,干扰零陷深度变浅等。即在幅相误差影响中,主要是相位误差在影响波束以及DOA估计的性能。

图3 相位误差情况下的波束图

图4 相位误差情况下的DOA估计

图5 幅相误差情况下的波束图

图6 幅相误差情况下的DOA估计
[1]IOANNIDES P,BALANIS C A.Uniform circular arrays for smart antennas[J].Antennas and Propagation Magazine,2005,47 (4):192-206.
[2]张会芝,杨育捷,王鲜芳.一种约束稳定性最小均方波束形成算[J].电光与控制,2014,21(3):129-132.
[3]韩国玺,刘春生,张智.变步长LMS自适应滤波算法及其分析[J].舰船电子对抗,2010,33(1):112-114.
[4]杨蓓蓓.随机误差对数字波束形成系统性能的影响[J].信息化研究,2010,36(3):9-12.
[5]田怡.智能天线阵列的误差分析建模与校准算法[J].通信电源技术,2014,31(1):102-103.
[6]WUZJ,YEN.Analysis of the wavelet adaptive algorithm in smart antenna system for 3G[C].[s..n.]:WMSVM,2010:188-190.
[7]闫冰冰.稳健的自适应波束形成计算研究[D].合肥:安徽大学,2012.
[8]DU L,LI J,STOICA P.Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):449-458.
[9]魏婵娟,刘鹏.一种阵列天线幅相误差校正方法设计[J].电子设计工程,2012,20(24):47-50.
[10]ASL B M,MAHLOOJIFAR A.Contrast enhancement of adaptive ultrasound imaging using eigenspace-based minimum variance beamfoming[J].IUS,2009(5):349-352.
[11]赵英俊,李荣锋,王永良,等.一种基于降秩变换的ESB改进算法[J].现代雷达,2013,35(9):20-23.
(责任编辑:朱联九)
Analysis and Study of the Affection of Array Error on Smart Antenna Algorithm Performance
WU Mei-yu,LIU Chi-biao
(IOT Application Engineering Research Center of Fujian Province Colleges and Universities, School of Information Engineering,Sanming University,Sanming 365004,China)
The system capacity of IOT and spectrum utilization of wireless communication systems can be improved by smart antenna technology.Array amplitude and phase error model is established in this paper and then robustness analysis of ESB algorithm is given to explore the effect of array amplitude and phase error on algorithm performance.Also the analysis by MATLAB simulation is given.Experimental results show that array amplitude and phase error does not make the actual array direction vector under ideal conditions any longer,which will seriously affect the performance of smart antenna system.
smart antennas;amplitude and phase error;performance affection;ESB algorithm
TN821.91
A
1673-4343(2014)04-0024-04
10.14098/j.cn35-1288/z.2014.04.005
2014-03-09
三明学院青年教师科研基金项目(B201204/Q);福建省教育厅科技项目(JA13299)
吴美瑜,女,福建大田人,助教。研究方向:物联网工程、物联网安全、网络工程。
