Grassmann 流形上半监督特征映射算法及其视频目标识别

李淑芳，曾宪华，冯萧

(1.重庆邮电大学计算机科学与技术学院，重庆 400065;2.重庆邮电大学计算智能重庆市重点实验室，重庆 400065)

0 引言

随着监控技术的发展，视频采集设备越来越方便和普及，视频具有时空信息丰富、存储量大、处理时间长等特点，使得视频目标识别成为机器学习、模式识别、计算机视觉、智能监控等领域的研究热点。丰富的视频数据使得子空间成为一种有效的特征表示方法，使用子空间集描述视频集具有如下优点:①由多幅视频帧张成的子空间比单帧图像包含更多的信息;②采集的视频可能长短不一，可使用子空间描述每段视频的共性，这是一种粗粒度描述方式，由视频组成的数据集合的学习问题就可转化为在Grassmann流形上的子空间学习问题;③当视频数据集非常大时，利用2个子空间进行比较，与直接比较2段视频相比，更简单、更有效;④由于子空间可以“填补”视频中丢失的信息，故对于有部分信息丢失的数据这种方法有更强的鲁棒性。利用子空间的主角度有利于提高目标识别模型的准确性、效率、鲁棒性［1－2］。

空间组成的数据可看成采样自Grassmann流形上点的集合(由子空间组成)，一个子空间就是Grassmann流形上的一个点［1］，Grassmann流形框架下的子空间学习问题是一个研究热点，这些研究方法主要是采用线性方法将视频集对应子空间集合进行相似性度量，广泛应用于目标识别、形状不变性识别、聚类等［3－15］。目前通过子空间的主角度实现目标识别最为典型的方法是由O.Yamaguchi和K.Fukui等提出的互子空间方法(mutual subspace method，MSM)［8］，该方法直接通过子空间的相似度(主角度或相关关系来计算)进行最近邻分类，实现数据集合之间的分类，如图像集、视频等问题的分类;后来，K.Fukui和 O.Yamaguchi进一步将表示每一个描述数据集合的子空间都投影到一个差异子空间，从而提出了约束互子空间方法(constrained mutual subspacemethod，CMSM)［9］，该方法将每个子空间投影到这个差异子空间获得新的子空间集表示，然后再实施MSM步骤，性能有所提高;最近，T.K.Kim等在PAMI上发表研究成果，他们将线性判别分析应用到训练有标记的子空间集合，发现子空间的投影变换矩阵，从而提出了相关关系鉴别分析(discriminant－analysis of canonical correlations，DCC)及其扩展［10－11］，通过求变换关系，子空间的基构成的列正交矩阵进行投影变换后，将子空间的类内的相关关系最大化，同时最小化子空间的类间相关关系;并且他们还进一步扩展应用典型相关关系度量视频之间相似性，并在动作识别应用方面取得了很好的效果。这些方法基本上是对子空间的相似性直接度量或是经过某种线性变换后再度量，从而实现识别的方法。实际上子空间集合可能并不分布在一个线性Grassmann流形上，非线性的变换方法可能更为合理。本文采用半监督的拉普拉斯特征映射融合了Grassmann流形上子空间集合之间几何分布性质、子空间中心之间的相似度关系以及有标记子空间的类别信息，提出了一种新的非线性方法，即基于Grassmann流形的半监督特征映射算法(grassmann manifold－based semi－supervised feature mapping algorithm，GMSFM)。该方法融合视频集合的几何分布、中心位置以及标记信息，通过将Grassmann流形上子空间转化为低维欧氏空间中低维流形上的坐标点，使得每个视频序列对应欧氏空间中的一个低维坐标点。然后，把对应的低维坐标点作为相关分类器的输入，这样可以降低训练分类器的复杂度，保持视频集几何分布的基础上融入部分视频序列的标记信息可以提高识别性能。在著名的步态视频数据库、人手姿势视频数据库和物体姿势视频数据库上作了较丰富的比较实验，实验表明了本文方法的优越性能。

1 基于Grassmann流形的半监督特征映射算法(GMSFM)

视频集合的每一个视频可以对应Grassmann流形上一个点(即一个子空间)，针对传统的子空间集合上学习方法是直接度量或通过某种线性变换后计算子空间之间的主角度来度量视频间的距离关系。实际上子空间集合可能并不分布在一个线性Grassmann流形上，所以子空间集合非线性地映射成欧氏坐标点集是一个合理方式，本文采用改进的拉普拉斯特征映射，融合了Grassmann流形上子空间集合之间几何分布性质、子空间中心的相似度关系以及有标记子空间的类别信息，提出了一种针对子空间集的非线性特征映射方法，即Grassmann流形上的半监督特征映射算法并应用于视频目标识别。基于Grassmann流形上的半监督特征映射算法的视频目标识别流程如图1所示。首先采用主成分分析法(principal component analysis，PCA)提取每个视频序列的子空间特征(如果一个视频序列形成一个非线性流形可以通过局部曲率阈值分割成子视频序列，再应用PCA进行处理)，每个视频序列对应保存子空间的基和该序列的均值图像;其次，计算2个视频序列的度量，包括3个部分的融合，即子空间之间的度量使用性能好且计算方便的Projection度量、序列间均值图像的度量采用余弦度量、有标记序列的标记信息α的强化。同时，约束同类视频序列之间相似度大于0.5，不同类之间相似度小于0. 5;然后，采用具有聚类特性的局部近邻度量保持的拉普拉斯特征映射算法;最后，利用低维欧氏坐标及其标记训练分类器做识别。

2.3.1 推荐对于消化道出血风险高危的患者DAPT治疗联用PPI(Ⅰ,B)[9]：虽然使用PPI不增加心血管事件风险的证据是有奥美拉唑研究获得，基于药物与药物相互作用研究，奥美拉唑和艾美拉唑似乎具有最高倾向的临床药物相互作用，而泮托拉唑和雷贝拉唑的药物相互作用倾向最低。

二是支持农民用水户协会发展。省财政、水利等部门联合出台《关于加强农民用水户协会建设的指导意见》，加强农民用水户协会的运作和能力建设，共建立农民用水户协会2 299个，实现了农民用水户协会“政府指导、自主管理、互利互惠”的建设成效。

GMSFM的详细步骤如下。

实验1是在步态视频数据库上完成，实验数据来自于著名的CASIA步态视频数据库A［15］，由于该数据库中目标行走路径差异大，实验中对20人在水平行走方向(如图3a)采集到的80个视频序列进行实验，每个视频序列的帧数分布在37－127帧之间。实验中根据对称性将每人步态视频都处理成从右到左行走的4个视频序列，采用留一法交叉验证，每类的3个序列作为有标记的训练集(共60个视频序列)，每类剩下的1个序列为无标记的测试集(共20个视频序列)。为了节约存储每帧缩放为30×44且像素值转化为［0，1］区间的灰度值，每个不同长度的视频序列通过PCA获得20维的线性子空间并保存每个视频序列的均值图像，采用最简单的最近邻分类器。在本文的GMSFM算法中子空间相似度与中心相似度的平衡因子β=0.8，最近邻数k=7，主角度个数为5时，图3b是一次实验在类别信息强化指数α∈(0，1)的不同取值及不同嵌入维数时的识别率曲面(单次最高识别率达到90%)。为了和MSM，CMSM，DCC等相关算法进行比较，采用简单的最近邻分类器，多次实验获取5个主角度最优，采用留一法交叉验证进行4次实验，最好识别率平均分别为65%，67.5%，73.75%(如表1所示)，本文算法在主角度个数为5，β=0.8，k=7时的平均最佳识别率81.25%，优于其他3种算法。

图2 类别信息强化前后的相似度Fig.2 Similarity of category information and enhanced category information

2 实验结果与分析

实验2是在剑桥人手姿势视频数据库的Set1视频集合上完成，实验数据集包括由9种人手姿势变化(如图4a所示)采集到的180个视频序列，每种姿势变化为一类，每类20个视频序列。实验中每一个序列40帧，每帧尺寸为30×40像素，每个像素转化为［0，1］区间的灰度值，为了便于实验重现，每类前10个序列作为有标记的训练集(90个视频序列)，另10个序列为无标记的测试集(90个视频序列)。每个视频序列通过PCA获得20维的线性子空间来描述，这样每段视频对应的子空间就可以看成Grassman流形上的一点。在本文算法中子空间相似度与中心相似度的平衡因子β=0.8，最近邻数k=10，主角度个数为5时，图4b是实验在类别信息强化指数α∈(0，1)的不同取值及不同嵌入维数时的识别率曲面。为了和MSM，CMSM，DCC等相关算法比较，采用最近邻分类器，多次实验取5个主角度最优，本文算法在主角度个数为5，β=0.8，k=7，α=0.05，欧氏嵌入空间维数为7时获得了4种算法中的最高识别率76.667%，而MSM算法的识别率只有60%，CMSM要求投影到450维子空间才获得最好识别率64.44%，DCC算法要投影到80维子空间才获得最好识别率73.33%，本文算法只需投影到7维欧氏嵌入空间就能获得4种算法中最好识别性能(识别率达到76.667%)。

低维嵌入坐标由LE算法中拉普拉斯矩阵L=D－M的特征方程Lu=λDu的最小d个非零特征值对应的特征向量计算，等价于特征方程Mu=λDu的第2到第d+1个最大特征值对应的特征向量(稳定的求解方法)，其中M是前面计算的半监督相似度矩阵，对角矩阵D的对角线元素为Dii=∑jMij。

实验3是在著名的ETH－80视频数据库上完成，实验数据集由8种对象的不同姿势变化采集到的80个视频序列，每种对象为一类由10个视频序列组成，每一个视频序列是在同一光线条件下从41个视角采集到41帧。图5显示了每类一个序列的2种视角。

图3 本文算法在CASIA步态视频数据库A的实验Fig.3 Experimental by using GMSFMalgorithm on CASIA gait database A

本节将在常用的中科院步态视频数据库［16］(institute of automation，Chinese academy of sciences，CASIA)、剑桥人手姿势视频数据库［17］和 ETH－80 物体姿势视频数据库［18］上验证本文算法性能，和几种典型的基于子空间相似性的分类算法(包括MSM，CMSM，DCC)作了比较实验，结果如表1所示。

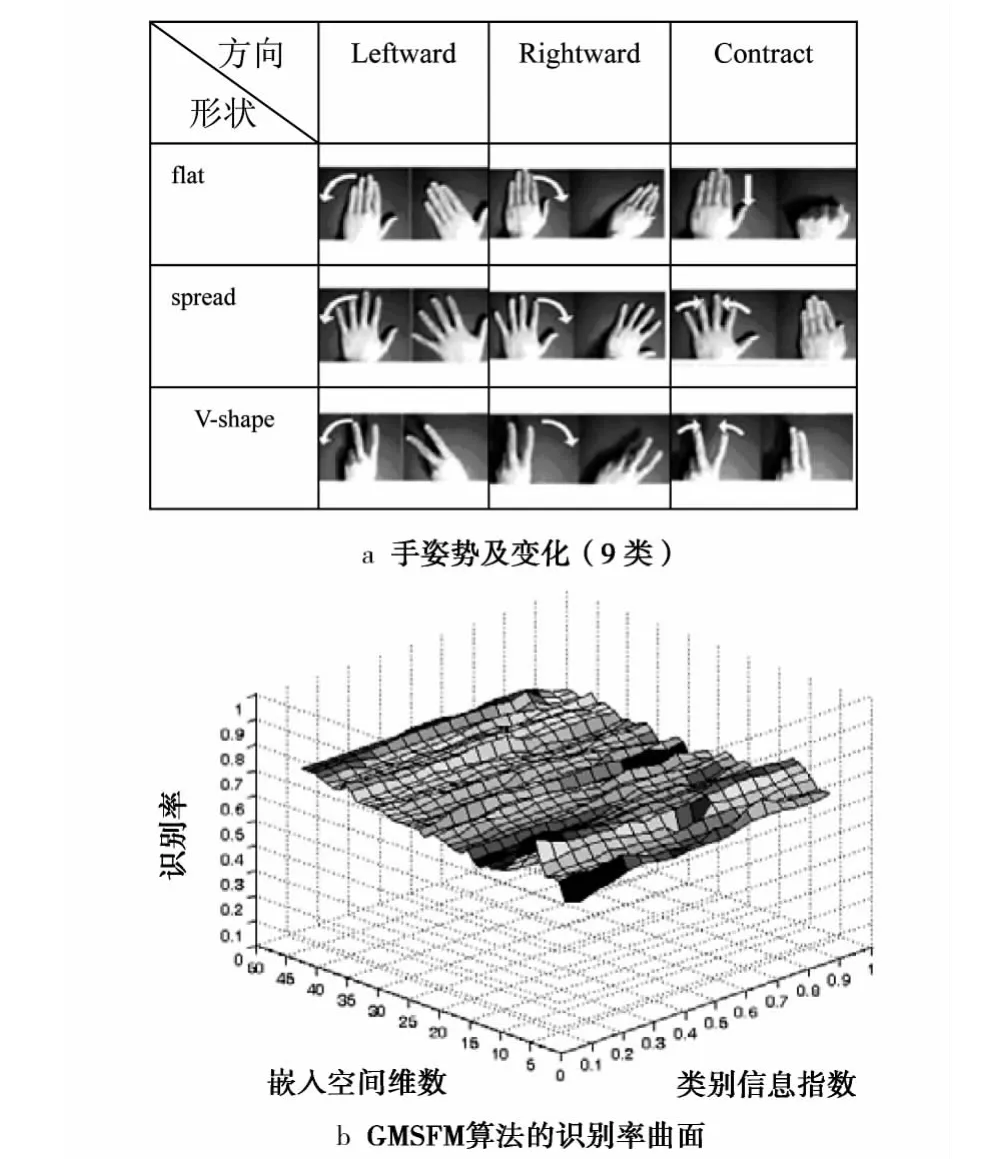
图4 本文算法在剑桥人手姿势视频数据库的实验Fig.4 Recognition rate surface by using GMSFMalgorithm on Cambridge hand gesture database

如今，鄌郚镇的电声乐器生产水准已经居于国际领先地位。经过几十年的发展，到目前鄌郚镇已拥有乐器及其配件生产企业超过80家，从业人员四千多人，产品包括电吉他、电贝司、木吉他、木贝司、音箱和乐器配件等6大系列，近400个花色品种，年产乐器300万把，产值达15亿元，产品主要销往韩国、日本、美国、澳大利亚等30多个国家和地区。全镇乐器企业拥有“雅特”、“仙乐”、“feeling”、“大树”等近40个品牌。其中“feeling”、“仙乐”电吉他被评为“山东名牌产品”和“山东著名商标”。鄌郚镇已成为山东大学、山东师范大学、山东艺术学院等高校的实践教学基地，也是中国电声乐器产业基地。

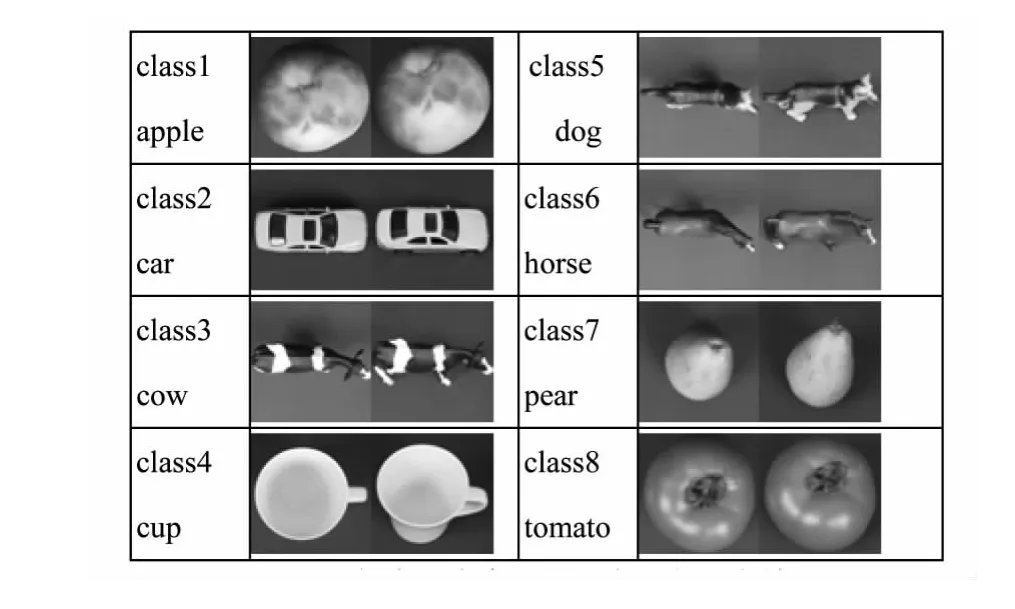
图5 每类一个序列的2个视角对应帧Fig.5 Two images of one image sequence from each class

实验中每一个序列的41帧图像的尺寸为32×32像素，每个像素转化为［0，1］区间的灰度值，为了便于实验重现，每类4个序列作为有标记的训练集(32个视频序列)，每类剩下的6个序列为无标记的测试集(48个视频序列)。每个序列通过PCA获得20－维的线性子空间来描述，这样每段视频对应的子空间就可以看成Grassman流形上的一点。在本文算法中子空间相似度与中心相似度的平衡因子β=0.8，最近邻数k=10，主角度个数为5时，图6是在类别信息强化指数α∈(0，1)的不同取值及不同嵌入维数时的识别率曲面。

图6 本文算法在ETH－80上的识别率曲面Fig.6 Recognition rate surface by using GMSFMalgorithm on ETH－80 database

为了和MSM，CMSM，DCC等相关算法比较，分类器采用的都是简单的最近邻分类器，实验中都取5个主角度，本文算法在主角度个数为5，β=0.8，k=10，α=0.1，欧氏嵌入空间维数为8时的最佳识别率达87.5%，而MSM算法的识别率只有79.92%，CMSM要求投影到130维子空间和DCC算法要投影到55维子空间才均获得最好识别率83.33%，本文算法只需投影到8维欧氏嵌入空间能获得4种算法中最好性能(识别率达到87.5%)。

3 结论

本文采用半监督特征映射将视频集非线性地映射到低维欧氏空间，提出了基于Grassmann流形的半监督特征映射算法(GMSFM)，综合了视频集合的几何分布、中心位置以及标记信息，获得的低维欧氏低维表示有利于分类识别。在步态视频数据库、人手姿态数据库和ETH－80进行实验，识别结果分别达到了81.25%，76.667%和87.5%，结果证实该算法比著名的MSM，CMSM和DCC算法有更好的识别性能。但是相似度的计算融入了子空间的几何分布信息、视频序列中心距离信息、视频标记信息，对相关参数的选取还没有理论依据，下一步工作是探索它们的自适应选取方法。另外，分布在非线性流形上的视频分割成线性的子视频序列集也是将来要做的工作。

根据表1和表2的数据，能够得出这样的结论：在该测区里，全部的检查点中误差以及基本定向点残差都是合乎要求的，其绝对定向精度已经合乎生产1∶2000 DOM的要求。

［1］HAMM J.Subspace－based learning with Grassmannmanifolds［D］.Philadelphia:University of Pennsylvania，2008.

［2］KIM T K.Discriminant Analysis of Patterns in Images，Image Ensembles，and Videos［D］.British:University of Cambridge，2007.

［3］LU Jiwen，YANG Gao，TAN Y P.Robust gait recognition via discriminative set matching［J］.Journal of Visual Communication and Image Representation，2013，24(4):439－447.

［4］TURAGA Pavan，VEERARAGHAVAN Ashok，SRIVASTAVA Anuj，etal.Statistical Computations on Grassmann and Stiefelmanifolds for Image and Video－Based Recognition［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2011，33(11):2273－2286.

［5］SI Si，TAO Dacheng，GENG Bo.Bregman Divergence－Based Regularization for Transfer Subspace Learning［J］.IEEE Transactions on Knowledge and Data Engineering，2010，22(7):929－942.

［6］ZENG Xianhua，ZHONG Jingjing.Semi－supervised Discirminative Mutual Subspace Method［EB/OL］.(2011－10－08)［2013－02－11］.http://www.researchgate.net/publication/224257971_Semi－Supervised_Discriminative_Mutual_Subspace_Method.

［7］WANG Ruiping，SHAN Shiguang，et al.Manifold－Manifold Distance with Application to Face Recognition based on Image Set［C］//Computer Vision and Pattern Recognition.USA:Anchorage，AK，IEEE Conference，2008:2940－2947.

［8］YAMAGUCHIO，FUKUIK.Face recognition using temporal image sequence［C］//Automatic Face and Gesture Recognition.Florida USA:Third IEEE International Conference on IEEE，1998:318－323.

［9］FUKUIK，YAMAGUCHIO.Face recognition usingmultiviewpoint patterns for robot vision［M］//Springer Berlin Heidelberg:Robotics Research，2005:192－201.

［10］KIM TaeKyun，KITTLER J，CIPOLLA R.Discriminative Learning and Recognition of Image Set Classes Using Canonical Correlations.IEEE Trans［J］.Pattern Analysis and Machine Intelligence，2007，29(6):1005－1018.

［11］KIM TK，CIPOLLA R.Canonical Correlation Analysis of Video Volume Tensors for Action Categorization and Detection［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2009，31(8):1415－1428.

［12］刘云鹏，李广伟，史泽林.基于Grassmann流形的仿射不变形状识别［J］.自动化学报，2012，38(2):248－258.

LIU Yunpeng，LIGuangwei，SHI Zelin.Affine－invariant Shape Recognition Using Grassmann Manifold［J］.Acta Automatica Sinica，2012，38(2):248－258.

［13］蔺广逢，朱虹，范彩霞，等.基于Grassmann流形的多聚类特征选择［J］.计算机工程，2012，38(16):178－181.

LIN Guangfeng，ZHU Hong，FAN Caixia，et al.Multicluster Feature Selection Based on Grassmann Manifold［J］.Computer Engineering.2012，38(16):178－181.

［14］曾宪华.流形学习的谱方法相关问题研究［D］.北京:北京交通大学，2009.

ZENG Xianhua.Study on Several Issues of Spectral Method for Manifold Learning［D］.Beijing:Beijing Jiaotong University，2009.

［15］MAO Yu，ZHOU Yanquan，LIRuifan，etal.Semi－supervised learning via manifold regularization［J］.The Journal of China Universities of Posts and Telecommunications，2012，19(6):79－88.

［16］中国科学院自动化研究所.CASIA步态数据库［EB/OL］.(2005－07－08)［2013－01－12］.http://www.cbsr.ia.ac.cn/china/Gait%20Databases%20CH.asp.

Institute of Automation，Chinese Academy of sciences.CASIA gait database［EB/OL］.(2005－07－08)［2013－01－12］.http://www.cbsr.ia.ac.cn/china/Gait%20Databases%20CH.asp.

［17］KIM T K，WONG S F.Tensor Canonical Correlation A－nalysis for Action Classification，In Proc.of IEEE Conference on Computer Vision and Pattern Recognition［EB/OL］.(2007－10－12)［2013－01－21］.http://www.iis.ee.ic.ac.uk/～tkkim/ges_db.htm.

［18］LEIBE Bastian，SCHIELE Bernt.Analyzing Appearance and Contour Based Methods for Object Categorization.In International Conference on Computer Vision and Pattern Recognition［EB/OL］.(2003－12－12)［2013－01－21］.http://people.csail.mit.edu/jjl/libpmk/samples/eth.html.

(编辑:田海江)