基于瞬时空腔效应的明胶靶标与肌肉目标等效性研究

金永喜，买瑞敏，张敬敏，周克栋，曾鑫，崔海林，袁瑞

(1.中国兵器工业第208 研究所，北京102202;2.南京理工大学 机械工程学院，江苏 南京210094)

0 引言

瞬时空腔是弹头、破片等高速杀伤元侵彻机体过程中产生的主要物理现象。瞬时空腔体积、最大直径等典型特征量是判定杀伤元杀伤效能的重要依据。明胶靶标是一种均匀、透明的粘弹性介质，其瞬时空腔的物理响应不但与生物组织接近，而且便于采用高速摄影技术直接拍摄其演化过程。因此，明胶靶标作为肌肉组织模拟物被广泛应用于瞬时空腔效应的相关理论和实验研究。

瞬时空腔效应自20 世纪40 年代被提出以来，一直是创伤弹道学领域的研究重点，主要研究工作分为两个方面:一是从创伤医学方面［1-2］研究瞬时空间对肌肉目标的损伤机理;二是从终点弹道领域研究明胶内瞬时空腔效应与杀伤元特征量间的量效关系，并对杀伤效应进行评估。美国Letterman Army 研究所基于对明胶空腔效应的研究建立了用于评估武器弹药威力及鉴定枪伤的“创伤剖面图”方法［3］;Peters 等［4］建立了明胶最大瞬时空腔理论模型;Liu 等［5］、莫根林等［6］建立了空腔的运动演化模型;温垚珂等［7］采用显式有限元数值方法准确预测了明胶内瞬时空腔的演化过程。

国内外针对明胶靶标与肌肉目标杀伤效应(瞬时空腔效应等)间的等效关系研究还不够充分。Janzon 等［8］从密度和组织成分角度分析认为明胶靶标模拟肌肉目标较为合理;Yoganandan 等［9］从生物力学角度分析认为二者的弹道阻力相近。这些研究仅从定性观察角度出发，缺乏系统全面的实验数据支撑，未建立明胶靶标与肌肉目标间的定量相似关系模型。

本文以瞬时空腔效应为研究对象，从瞬时空腔形成的物理过程入手，找出影响瞬时空腔尺寸的主要物理参数，采用相似理论推导出不同介质内空腔典型特征量的相似准则方程，从而建立瞬时空腔效应的等效模型，并求解出模型的系数，最后通过生物实验验证了等效模型的准确性。

1 最大瞬时空腔等效模型

1.1 瞬时空腔膨胀过程及最大直径影响因素分析

本文采用球形破片作为杀伤元开展研究工作，可以排除杀伤元自身不稳定因素对研究对象的影响，便于研究过程的分析及数据处理。

球形破片侵彻软质目标形成的瞬时空腔运动如图1 所示，首先对目标介质产生切割破坏，同时使杀伤元-目标界面的质点产生速度，从而在一定范围内形成速度场，推动临近介质产生径向运动，介质粒子的动能逐步转换为软质目标的弹性势能，瞬时空腔开始膨胀。因此瞬时空腔的形成过程可分为，目标的初始能量获取过程和目标内空腔的膨胀过程两部分。对于球形破片，其最大空腔直径位于入口位置，本文的研究重点是最大空腔直径的等效性，因此取弹道入口处的目标薄片微元进行分析。

能量传递过程即杀伤元侵彻过程，能量传递过程在侵彻距离上是连续的，忽略微元与其后部目标间的相互影响，假设入口微元厚度为Δx，杀伤元损失的动能全部转化为目标介质的动能，杀伤元损失ΔEp可根据刘坤等［10］的破片侵彻运动模型推导获得，则入口微元吸收的能量ΔEt为

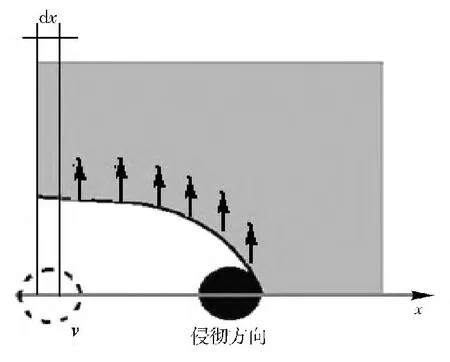
图1 高速钢球侵彻软质目标后的空腔运动状态Fig.1 The movement of cavity in soft target after high speed steel-ball penetrating

式中:ρp为杀伤元密度;d 为杀伤元直径;ρt为软质目标密度;v0为球形杀伤元初始速度;CD为球形杀伤元在软质目标中的阻力系数。

瞬时空腔膨胀过程较为复杂，国内外相关研究多为空腔尺寸经验公式和数值计算，Zeng 等［11］忽略目标粘性所消耗的能量，假设空腔膨胀过程为目标吸收的能量转化为弹性势能，获得空腔最大直径时刻的弹性势能与目标尺寸特征的关系，如(2)式所示。

式中:rmax为最大瞬时空腔半径;r0为空腔初始尺寸(球形破片半径r0=d/2);R0为目标初始半径(肌肉或明胶靶标初始外部尺寸);pa为大气压力;Δx 为目标微元厚度;E 为靶标杨氏模量;ψ 为空腔内部的真空度;C1、C2、C3为中间变量，分别为C1=(-

忽略空腔膨胀过程目标粘性消耗的能量，可认为最大空腔时刻的弹性势能等于目标吸收的能量，即

将(1)式、(2)式代入(3)式可得

从(4)式可得最大瞬时空腔尺寸(半径rmax)与杀伤元的密度ρp、速度v0、直径d，目标的杨氏模量E、密度ρt、目标初始半径(肌肉或明胶靶标初始外部尺寸)R0，及大气压力pa、空腔内部的真空度ψ 等变量相关。

1.2 典型物理特征量相似准则方程的推导

根据相似第二定理(π 定理)，球形侵彻肌肉、明胶靶标时造成的瞬时空腔的最大直径与其影响因素的函数依存关系为

由(5)式可列出因次分析矩阵，参数表如表1所示。

表1 变量因次分析表Tab.1 The values of exponential

表1 中独立变量数为8，矩阵的秩为3，于是，导出的独立准则数应该为8 -3 =5. 根据物理方程的因次和谐原则，并以密度ρp、速度v0、直径d 作为基本量，对(5)式进行求解，然后按相同指数归并后，即得出关于瞬时空腔最大直径Dmax的无因次相似准则方程:

式中:K、A1、A2、A3、A4、A5为待定系数(无量纲常数)。

(6)式代表的是基于前述过程假设的所有软质目标的空腔效应准则方程，钢球侵彻不同目标瞬时空腔最大直径的相似可以假设为模型和原型之间的相似。设肌肉目标用下标“1”表示，明胶靶标用下标“2”表示，则有

本文的目的是研究在杀伤元状态相同的条件下，明胶与肌肉瞬时空腔最大直径的等效关系，故d1=d2;10%明胶靶标密度(1.03 g/cm3)与肌肉目标密度(1.04 g/cm3)相近，可近似认为ρt1=ρt2;研究过程去除目标尺寸的影响，即不同目标的外径尺寸相同R01= R02;实验在同一种环境下进行pa1=pa2，ψ1=ψ2;用(7)式除以(8)式，得到:

式中:K12=K1/K2为常系数，可由实验数据求出。

1.3 等效模型系数的确定

由(9)式可知，要建立相同杀伤元侵彻不同材料目标时最大瞬时空腔直径之间的等效关系，需测出不同目标的材料特性参数E，求解系数K12和指数系数A2.

明胶靶标为温度敏感材料，其杨氏弹性模量随温度改变而明显改变。因此可以采用不同温度明胶靶标获得对应温度下的弹性模量与最大瞬时空腔直径数据，并采用活体生物后肢获得一组肌肉靶标的弹性模量与最大瞬时空腔直径数据，从而求解出等效方程的2 个系数。

实验杀伤元采用直径4.8 mm、速度1 200 m/s左右的球形破片。明胶靶标空腔直径数据获取实验如图2 所示，利用高速摄影技术获取瞬时空腔最大直径(见图3)。明胶靶标配比为10%，尺寸为30 cm×30 cm × 30 cm，温度分别为4 ℃、10 ℃、15 ℃;高速摄影设备的型号为PhantomV710，拍摄帧频为2 ×104s-1. 弹性模量数据采用单轴压缩实验机获取，如图4 所示。生物肌肉空腔直径数据获取如图5所示，实验选择50 ～60 kg 猪的双后肢，以保证与明胶靶标尺寸相接近，利用高速脉冲X 光机记录猪腿靶标中的瞬时空腔形态(见图6)，猪腿部肌肉的弹性模量为82 792 Pa［12］。实验数据如表2 所示。

图2 模拟实验示意图Fig.2 Schematic diagram of simulation experiment

图3 不同温度下明胶靶标空腔Fig.3 The temporary cavities of gelatin targets at different temperatures

图4 明胶靶标弹性模量测试Fig.4 The elasticity-modulus test on gelatin

图5 生物实验示意图Fig.5 Schematic diagram of biology experiment

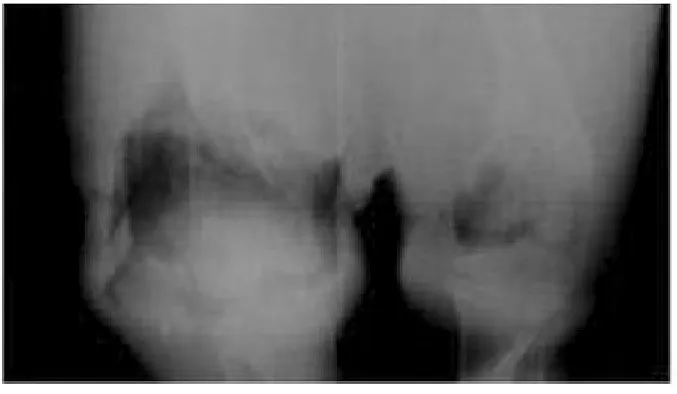
图6 生物实验中的最大瞬时空腔Fig.6 The max temporary cavity from pigs

为了便于数据处理，可以先将(9)式对数化:

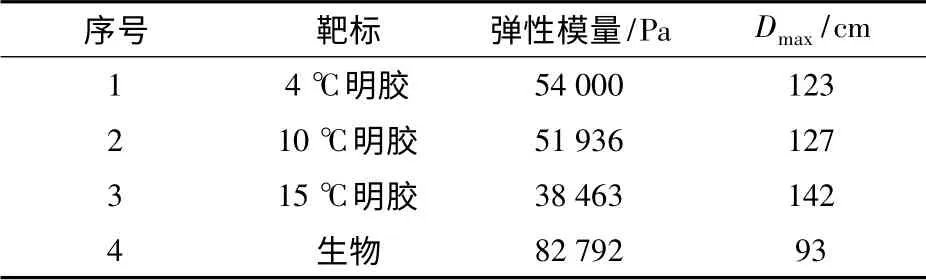
表2 不同目标的弹性模量及空腔最大直径数据表Tab.2 The temporary cavity and elasticity-modulus data of different targets

利用表2 实验数据采用按最小二乘法原理，解得K12=0.963、A2= -0.528 5，(10)式即为

2 最大瞬时空腔等效模型实验验证

采用实验手段进一步验证生物实验与明胶靶标实验对比的方法，验证等效公式(11)式的工程应用性和准确性。

通过调整破片速度，获得不同速度杀伤元的明胶靶标和生物实验数据，空腔数据获取方法如上述图2、图5 所示。分别采用直径4.8 mm 球形破片800 m/s、1 000 m/s 两组不同速度杀伤元进行实验研究。实验效果如图7 所示，实验数据如表3 所示。

图7 生物实验与明胶靶标中的最大瞬时空腔(上为猪腿部，下为明胶)Fig.7 The max temporary cavities formed in pigs(upper)and gelatin (below)

表3 实验获得的最大空腔直径数据表Tab.3 The max diameter temporary cavity from experiment

设Dmax，m、Emax，m为肌肉内最大瞬时空腔直径和弹性模量，Dmax，g、Emax，g为实验获得4 ℃明胶靶标的最大空腔直径和弹性模量，将上述参数带入(11)式可得

将表2 明胶靶标及猪腿部肌肉弹性模量数据代入(12)式可得

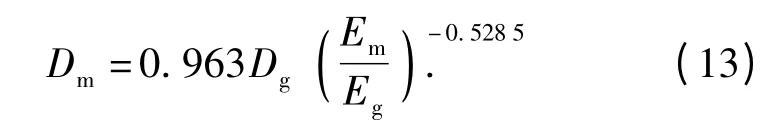
将表3 的明胶瞬时空腔直径代入(13)式的等效模型可计算得出肌肉目标最大空腔直径的估算值，与生物实验对比最大误差为4.0%，如表4 所示。

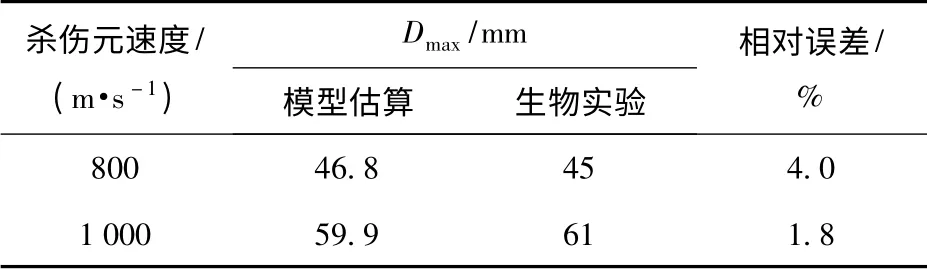
表4 模型预测与生物实验对比结果Tab.4 The comparison of model prediction and biology experimental data

3 结论

本文通过钢球杀伤元侵彻软质目标的瞬时空腔膨胀过程，提取影响最大空腔直径的主要物理参量，利用相似理论建立最大瞬时空腔直径相似准则方程，得出在杀伤元状态相同的条件下瞬时空腔最大直径与目标材料的弹性模量最为相关，并采用不同温度明胶靶标及生物肌肉目标的瞬时空腔与弹性模量对应实验数据，推导计算准则方程系数，建立了明胶靶标与肌肉目标瞬时空腔最大直径等效性模型。实验验证表明，采用该模型对明胶靶标瞬时空腔最大直径修正后的数据与生物实验获得的数据相对误差小于4.0%，从而验证了该等效模型具有较好的正确性与有效性，为明胶靶标的推广应用提供了理论参考。

References)

［1］刘荫秋，王正国，马玉媛. 创伤弹道学［M］. 北京:人民军医出版社，1991.LIU Yin-qiu，WANG Zheng-guo，MA Yu-yuan. Wound ballistics［M］. Beijing:People＇s Military Medical Press，1991. (in German)

［2］Kneubuehl B P，Coupland R M. Wound ballistics basics applications［M］.Berlin:Springer Medizin GmbH，2008.

［3］Fackler M L，Bellamy R F，Malinowski J A. The wound profile illustration of the missile-tissue interaction［J］.The Journal of Trauma and Acute Care Surgery，1988，28(1):S21 -S29.

［4］Peters C E，Sebourn C L. Wound ballistics of unstable projectiles.Part II temporary cavity formation and tissue damage［J］. The Journal of Trauma and Acute Care Surgery，1996，40(3S):16S-21S.

［5］Liu L，Fan Y，Li W，et. al. Cavity dynamics and drag force of high-speed penetration of rigid spheres into 10wt% gelatin［J］.International Journal of Impact Engineering，2012，50:68 -75.

［6］莫根林，吴志林，刘坤. 球形破片侵彻明胶的瞬时空腔模型［J］. 兵工学报，2013，34(10):24 -28.MOU Gen-lin，WU Zhi-lin，LIU Kun. Temporary cavity model of spherical fragments penetrating ballistic gelatin［J］. Acta Armamentarii，2013，34(10):24 -28 (in Chinese)

［7］温垚珂，徐诚，陈爱军，等. 步枪弹侵彻明胶靶标的数值模拟［J］. 兵工学报，2013，34(1):14 -19.WEN Yao-ke，XU Cheng，CHEN Ai-jin，et al. Numerical simulation of the penetration of bullet on gelatin target［J］. Acta Armamentarii，2013，34(1):14 -19.(in Chinese)

［8］Janzon B. Approximate theory on the cavity formation on projectile impact in dense media，FOA-C-20196-D4［R］. Stockhom:Research Institute of National Defence，1978.

［9］Yoganandan N，Pintar F A. Biomechanics of penetrating trauma［J］. Critical Reviews in Biomedical Engineering，1997，25(6):485 -501.

［10］刘坤，吴志林，徐万和，等. 球形破片侵彻明胶修正力学模型［J］.南京理工大学学报，2012，36(5):25 -31.LIU Kun，WU Zhi-lin，XU Wan-he，et al. Correction mechanical model of spherical fragments penetrating gelatin［J］. Journal of Nanjing University of Science and Technology，2012，36(5):25 -31.(in Chinese)

［11］Zeng Xin，Zhou Ke-dong，He Lei. Study on the influencing factors effecting temporary cavity caused by a high speed steel ball when penetrating into gelatin［J］.Advanced Materials Research，2012，532/533:110 -114.

［12］王宝珍，郑宇轩，胡时胜.猪后腿肌肉的动态拉伸性能［J］.爆炸与冲击，2010，30(5):449 -455.WANG Bao-zhen，ZHENG Yu-xuan，HU Shi-sheng. Dynamic tensile properties of porcine ham muscles ［J］. Explosion and Shock Waves，2010.30(5):449 -455.(in Chinese)