一类伪分形网络的生成树的计数

李姗姗,孙伟刚

(1.山东体育学院基础理论系，山东济南,250102；2.杭州电子科技大学理学院，浙江杭州,310018)

一类伪分形网络的生成树的计数

李姗姗1,孙伟刚2

(1.山东体育学院基础理论系，山东济南,250102；2.杭州电子科技大学理学院，浙江杭州,310018)

利用电阻等效转化方法，得到了一类伪分形网络前后两代生成树的加权函数所满足的递推关系,利用此关系,得到了这类伪分形网络的生成树计数的解析解,并用Kirchhoff矩阵-树定理验证了此生成树计数关于前两代所得到的结果。

生成树；伪分形网络；电阻等效转化

连通的无圈图称为树，一个连通图的生成树是该图的极小连通生成子图。图的每个生成树都包含了图的所有节点，因此生成树的数目可以反映网络的可靠性。网络的生成树的计数问题是网络的一种重要动力学特性，它与网络的其它动力学特性都相关，如网络的同步、鲁棒性及网络的随机游走等。伪分形网络属于一类确定性网络。与随机网络相比，在确定性网络中节点与节点以概率为1来连接。由于确定性网络具有确定的网络拓扑结构，可以得到用于衡量网络拓扑特征的解析解，为验证随机网络的一些结果提供了一种新思路。伪分形网络具有规则的网络结构，其生成算法是基于边迭代，已有边在下一步迭代过程中产生新的节点。关于其生成树的数目在文献[3-8]中已有相关研究，其方法适用于计算自相似网络的生成树的数目，但对于结构较复杂密度较大的网路却很难得到网络的生成树数目的计算公式。本文采用文献[9]中的方法，利用电阻等效转化，把一个步迭代图转化为初始状态，得到这个转化过程中的转化因子和图的边权的变化规律，进而得到网络的生成树的数目的求解公式。

定义3 图1中第一步表示串联边到单边的电路等效转化；第二步表示并联边到单边的电阻等效转化，其中表示电导率。

图1 串联边和平行边到单边的电阻等效转化

1 模型描述

基于文献[10]中提出的伪分形网络结构，此网络的初始状态是由两个三角形，共用一个节点组成。在之后的迭代过程中，上一代中每条边都生成一个新的节点，每一个新生成的节点和它对应的边的两端相连。经过步迭代后的图形用表示，图2表示了其前三代的网络结构。由图形的对称性和生成树的定义，我们只需得到其子图的生成树的数目即可，这个子图在步的迭代图用表示。图3给出了其前3代图形。

图2 网络的前3代图形

图3 子图的前3代图形

2 生成树数目的计算

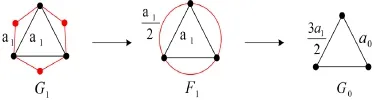
图4 图到的电阻等效转化过程

其中图G0是一个三角形，它的边权用a0表示。因此Gt的生成树的加权函数可以表示为其中

G，因为从图t到图Gt-1的转化因子为ft，所以从Gt到G0转化因子为

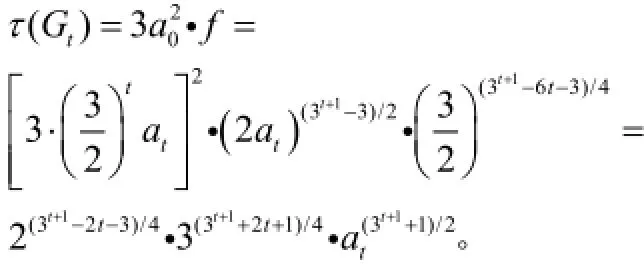
当at=1时，网络图Gt的生成树的数目的表达式是

根据图Γt由两个共用同一个节点的图Gt连接而成，由生成树的定义图Γt的生成树应由图Gt的两个生成树连接生成。因此图Γt的生成树的数目是:

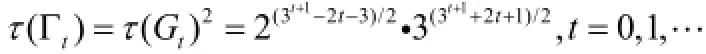
3 Kirchhoff矩阵-树定理检验

矩阵-树定理指的是G 的所有不同的生成树的个数等于其Kirchhoff矩阵(也称为拉普拉斯算子)任何一个n-1阶主子式的行列式的绝对值；也可以描述为生成树的个数等于矩阵的所有非0特征值的乘积除以网络中节点的个数。将图1中的Γ0和Γ1按下图等等所示，给每个节点编号（编号对计算结果无影响）。

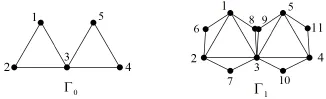
对于Γ0，它的节点度矩阵为

它的邻接矩阵为

则它的Kirchhoff矩阵为

同理，对于，它的Kirchhoff矩阵为

而当t=1时，τ(Γ1)=2916。因此当t=0和t=1时用两种方法算出的结果相同。可以看出Kirchhoff矩阵-树定理具有普遍适用性，但随着t 的增大，网络节点数不断增多，用Kirchhoff矩阵-树定理计算网络的生成树的数目将比较繁琐，甚至无法计算出结果，而本文采用的电阻等效转化的方法相比Kirchhoff矩阵-树定理要简便和更有效。

[1] 汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社，2006.

[2] 章忠志，周水庚，方锦清.复杂网络确定性模型研究的最新进展[J].复杂系统与复杂性科学,2008, 5(4):29-46.

[3] 霍玉洪，俞万禧，李晓毅.五面体平面图中的生成树的构造与计数[J].沈阳师范大学学报：自然科学版，2010, 28(2):148-150.

[4] 刘珊.扇图生成树的计数[J].咯什师范学院学报，2013,34(6):11-12.

[5] 俞万禧，李晓毅.奇阶完全图的生成树的构造与计数[J].渤海大学学报：自然科学版，2010, 31(2):133-137．

[6] 谭秋月.基于圈或路的多重星相关图的生成树数目[J].天津师范大学学报：自然科学版，2013,33(1):30-34.

[7] 谭秋月.基于圈的多重完全相关图的生成树数目[J].集美大学学报：自然科学版，2014,19(1):57-62.

[8] ZHANG Z Z,LIU H X,WU B,et al.Enumeration of spanning trees in a pseudofractal scale-free web[J].Euro Phys Lett,2010,90:68002.

[9] TEUFL E,WAGNER S.Determinant identities for Laplace matrices[J].Linear Algebra Appl,2010,432:441-457.

[10] DOROGOSTEV S N,GOLSTEV A V,MENDES J F F. Pseudofractal scale-free web[J].Phys Rev E,2002, 65: 066122.

Enumeration of Spanning Trees in a Family of Pseudo-fractal Networks

Li Shanshan1,Sun Weigang2
(1.Basic Theory Department,Shandong Sport University,Ji'nan,250102,China; 2.School of Science,Hangzhou Dianzi University,China)

We obtained a relationship for the weighted number of spanning trees in the successive two generations of a family of pseudo-fractal network by electrically equivalent transformations.Then we derive the analytical expression for enumeration of spanning trees.Finally,we verify the results of the first two generations by Kirchhoff matrix-tree theorem.

spanning trees; pseudo-fractal network;electrically equivalent transformation

O157.5

A

孙伟刚（1979-），男，山东青岛人，副教授，硕士生导师。

国家自然科学基金（61203155）

李姗姗，山东济南人，讲师。1981年10月，女，数学与应用数学、体育统计、高等数学、概率论与数理统计的教学。