RLS字典学习中遗忘因子的影响

余付平， 冯有前， 雷 腾， 李 哲

1.空军工程大学，西安710051

2.中国人民解放军94559部队，江苏徐州221000

近年来，信号稀疏分解已成为热点问题，并广泛应用于压缩感知[1]、图像处理[2-6]、信号去噪[6]、特征提取[7-8]等领域.其中，JPEG2000编码标准的成功也是由于自然图像的小波系数具有稀疏性.然而，信号稀疏分解的实现是一个难题，而过完备字典的构造是信号能否实现稀疏分解的关键因素.

目前，关于字典构造一般分为两大类：根据一定的先验知识构造固定的字典[4-5,9]；当没有先验知识或先验知识不足时，由样本训练的方法学习得到自适应的字典[2,7,10-11]. 字典学习方法主要包括最优方向法[12](method of optimal directions,MOD)、K奇异值分解(K singular value decomposition,KSVD)[3,11]、最大后验概率逼近(maximum A-posterior probability,MAP)方法[3,11]等.其中，MOD方法简单，但不适合处理大量数据；MAP方法在精确稀疏分解中能获得更好的恢复结果；KSVD方法在图像处理中得到了较好的效果，然而这些方法均受到初始字典较大的影响.为减小初始字典的影响，获得更好的字典，文献[10]提出了递归最小二乘(recursive least squares,RLS)字典学习方法.

1 稀疏分解理论

或者

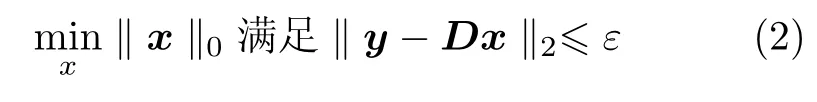
式中，‖·‖0表示向量中非零元素的数目.然而，上述问题的求解是一个NP难题.为了解决这个问题，许多稀疏分解算法被提出[14]，如匹配追踪(matching pursuit,MP)算法、基追踪(basis pursuit,BP)算法、框架方法(method of frames,MOF)和最优正交基(basis orthogonal best,BOB)算法.

2 RLS字典学习

2.1 字典学习的基本思路

给定一系列训练信号{yi,i=1,2,···,N}组成矩阵Y，训练信号yi在字典D上的分解系数表示为xi，则稀疏表示系数矩阵X={xi,i=1,2,···,N}，于是Y在字典D上的稀疏分解问题表示为

或者

字典学习通过一系列训练数据学习训练一个字典，使得训练信号在该字典上总体表示误差最小，从而使得训练得到的字典能够更好地适应所要解决的问题.因此，对于训练信号Y，寻找可能的最优字典的问题可以表示为

或者

本文根据式(6)分析字典学习问题，从而将字典学习问题转化为总体误差的最小化问题.针对一系列训练信号的字典学习主要包括两个步骤[10]：

步骤1 对于固定的字典D，求解使得总体误差R最小的分解系数X；

步骤2 根据求解的系数X，求解使得总体误差R最小的字典D.

2.2 引入遗忘因子w的RLS字典学习

固定分解系数X，求解R关于字典D的导数，使得总体误差最小，从而得到字典D的更新公式

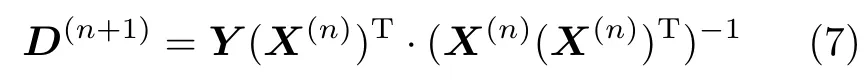
式(7)的字典更新方法被称为最优方向法(method of optimal directions,MOD).

当一个新的训练信号出现时，RLS方法均会更新字典.因此，这个算法首先假定已经存在i个训练信号，当第i+1个信号出现时，寻找新的字典更新公式.

假定Yi=[y1,y2,···,yi]，且矩阵大小为N×i，对应的分解系数Xi=[x1,x2,···,xi]，大小为K×i.根据式(7)得到

式中

当新的训练信号y=yi+1出现时，y在字典Di上的分解系数x=xi+1.根据式(8)得到

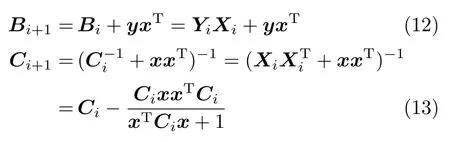
式中根据式(12)和(13)得到

定义向量µ=Cix和尺度则

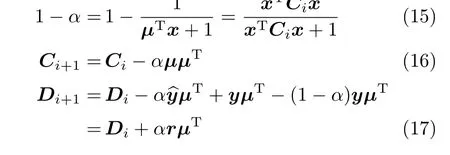
由式(17)可以看出，字典的更新受到表达误差r的影响.由上述分析可以看出，由于RLS方法在初始迭代时选取的初始字典难以准确反映样本信息，训练样本对应的表达误差r较大，可信度较低；随着新的训练样本的出现，字典逐步得到更新，于是对训练样本的表达效果也越好，新样本的表达误差r会较小，可信度较高.为了减小初始迭代阶段表达误差较大的影响，对初始阶段的表达误差乘以较小的遗忘因子.随着表达误差的减小，遗忘因子应该逐渐增大，则引入遗忘因子w的训练信号总体误差表示为

式中

由式(18)可以看出，初始训练样本的表达误差乘以较小的遗忘因子，随着样本的增加，遗忘因子逐渐变大.然而字典更新的实际过程为：初始字典对训练样本的表达效果有限，随着样本的增加以及字典的更新，更新字典对样本的表达能力更强，表达效果更好.为了减小初始字典对训练样本表达效果的影响，对不同训练样本的表达误差乘以不同的遗忘因子，使得初始训练样本的表达误差得到较小的信任度，随着新样本的引入，新样本的表达误差得到较大的信任度.引入遗忘因子后的上述情况与字典更新的实际情形更相符.同时，由于引入遗忘因子，初始样本对总体误差的贡献被消弱，所受到的初始字典的影响被消弱，字典更新过程能够更快地达到稳定.

根据式(18)可知，当遗忘因子取较小值时，样本表达误差大大消弱，但也影响样本本身信息的表达；而当遗忘因子取较大值时，样本信息得到充分表达，但样本误差也被充分体现，于是会影响字典学习效果.因此，需要选取合适的遗忘因子.引入遗忘因子后的RLS方法的字典更新公式为[10]

式中

尺度

3 仿真结果

由MATLAB仿真随机生成大小为20×50的初始字典，且字典的每一列均被归一化.随机生成训练数据库，大小为20×1 500，且具有稀疏性.从误差、字典距离、恢复比率、运行时间等衡量指标出发，研究不同方法的字典更新效果以及在RLS方法中遗忘因子对更新结果的影响.其中，误差为训练数据与重构数据之间差值的平方和；字典距离为学习字典列向量与真实字典列向量之间元素平方和的最小值；恢复比率表示每次迭代时字典距离大于0.99的原子数目；字典相似性表示更新字典与真实字典积矩阵的对角元素之和.

3.1 不同字典更新方法的仿真结果分析

通过200次迭代运算，得到如图1和2所示的仿真结果.图1给出了不同迭代次数时3种不同方法的表达误差.从图1中可以看出，随着迭代次数的增加，误差均下降.其中，KSVD和MOD方法表达误差下降的速度相近，且在迭代50次之后下降缓慢，接近稳定；RLS方法字典下降速度较快，且整体的误差均小于前两种方法，表达效果更好.图2给出了迭代次数与字典距离之间的关系.从图2中可以得到，随着迭代次数的增加，KSVD和MOD方法得到的更新字典与真实字典之间的距离逐渐下降，且两者的变化规律和大小比较接近.而随着迭代次数的增加，RLS方法得到的字典与真实字典之间的距离迅速减小，且每次迭代的距离值均小于KSVD和MOD方法的距离值.因此，RLS方法得到的字典与真实字典更相似，且对训练数据的重构表达效果更好.表1对比了3种不同字典更新方法的总恢复比率、字典相似性和运行时间.从表1中可以看出，RLS字典更新方法在总的恢复比率和字典相似性方面均优于KSVD和MOD方法.KSVD方法总体的运行时间最长，而MOD方法运行时间最短.

图1 分解误差随迭代次数的变化Figure 1 Decomposition errors variation with number of iterations

图2 不同迭代次数下的字典距离Figure 2 Dictionary distances of different number of iterations

综上所述，通过RLS字典学习方法得到的学习字典与真实字典更相似，与训练数据之间的相关性更强，表达训练样本的效果更好.

表1 3种字典学习方法的指标结果Table 1 Results of the indicators of three dictionary learning methods

3.2 不同遗忘因子的仿真结果分析

由于RLS方法在很多方面均优于KSVD和MOD方法，接下来主要讨论RLS方法.为分析RLS方法中不同遗忘因子对字典更新结果的影响，分别对固定遗忘因子和函数变量遗忘因子进行仿真.

3.2.1 固定遗忘因子的仿真结果

图3给出了遗忘因子取不同的固定值时分解误差随迭代次数的变化趋势.从图3中可以看出，随着迭代次数的增加，不同遗忘因子对应的误差均下降.遗忘因子w为0.995、0.990、0.985时误差下降得较快，且均明显优于遗忘因子w为1.000时的结果.当遗忘因子w为0.990、0.985时，误差变化趋势相近，但遗忘因子w为0.990时误差变化较平滑，抖动较小.图4给出了遗忘因子取不同的固定值时字典距离随迭代次数的变化趋势.对比图3和4可以看出，相同的遗忘因子对应的误差变化趋势与字典距离变化趋势相同.当遗忘因子w为0.990时，字典距离变化较快，且抖动较小.

表2对比了200次迭代后不同遗忘因子更新字典时的总恢复比率、字典相似性以及运行时间.从表2中可以看出，当遗忘因子w为0.990时，总的字典恢复比率以及字典相似性最大，更新字典与真实字典之间最相近，遗忘因子不同时运行时间差别很小.

图3 分解误差随迭代次数的变化Figure 3 Decomposition errors variation with number of iterations

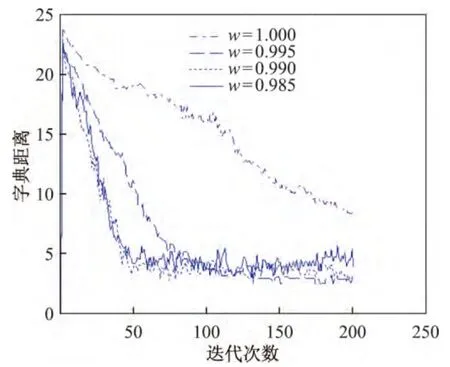
图4 字典距离随迭代次数的变化Figure 4 Dictionary distances of different number of iterations

表2 不同遗忘因子的指标结果Table 2 Results of the indicators of different forgetting factors

由以上分析可以得到，在RLS字典更新中，引入遗忘因子的字典更新效果优于遗忘因子恒等于1.000时的结果.同时，字典更新效果既不随遗忘因子的减小而变得更好，也不随遗忘因子的增加而变得更好，而是在遗忘因子w取0.990附近时相对较好.

3.2.2 遗忘因子为函数变量时的仿真结果

为了研究遗忘因子为函数变量时对字典更新结果的影响，分析了遗忘因子函数为w2=1-(1-0.990 )×(1-i/200)3、w3=1-0.08×0.2(i0.3)、w4=1-0.08×0.2(i0.4)时对应的仿真结果，并与w1=1时的结果进行对比.

图5和6分别给出了遗忘因子函数对应的分解误差以及字典距离随迭代次数的变化曲线.从图5和6中可以看出，当遗忘因子函数为w3和w4时，误差和字典距离的变化规律与w1=1时相似；当遗忘因子函数为w2时，误差和字典距离均优于遗忘因子函数为w3和w4时的结果，且经100次迭代后的误差值和字典距离变化幅度较大，几乎达到恒定.函数w3和w4曲率较大，而遗忘因子函数w2从0.990逐渐变化到1.000，从而说明函数值的变化曲率影响字典学习效果.

表3对比了3种遗忘因子取不同函数时的衡量指标.从表3中可以看出，选取不同函数时的运行时间差别很小；当函数为w2、w4时，字典相似性和总恢复比率较好.通过以上的分析可以看出，当遗忘因子为函数w2时，字典更新的总体衡量指标相对较好，与真实字典的相似性更强.

表3 遗忘因子为不同函数时的指标结果Table 3 Results of the indicators with different functions of the forgetting factor

图5 分解误差随迭代次数的变化Figure 5 Decomposition errors variation with number of iterations

图6 字典距离随迭代次数的变化Figure 6 Dictionary distances of different number of iterations

3.2.3 遗忘因子函数取不同圆周函数时的仿真结果

为了研究与3.2.2中函数w2类似的不同圆周函数的字典更新效果，分别分析了遗忘因子取3种不同曲度的圆周函数时的各种字典更新效果的指标.3种不同曲度圆周函数曲线为：w1=1-(1-0.990)×(1-i/200)3、w2=1-(1-0.990)×(1-i/100)3、w3=3-(1-0.990)×(1-i/250)3.

经过200次循环迭代，得到了遗忘因子取3种不同曲率圆周函数时对应的误差曲线和字典距离曲线，如图7和8所示.分析图7和8可以得出，3种函数对应的误差和距离的变化趋势几乎相同，差别很小；函数w3对应的误差下降速度在迭代次数100次附近加快，收敛效果稍好.当遗忘因子函数的曲率在一定范围内时，字典更新效果差别不大.表4对比了遗忘因子取不同圆周函数时的3种衡量指标.从表4中可以看出，取不同函数时的运行时间差别很小；在字典相似性和总恢复比率方面，遗忘因子为函数w3时结果较好.

图7 分解误差随迭代次数的变化Figure 7 Decomposition errors variation with number of iterations

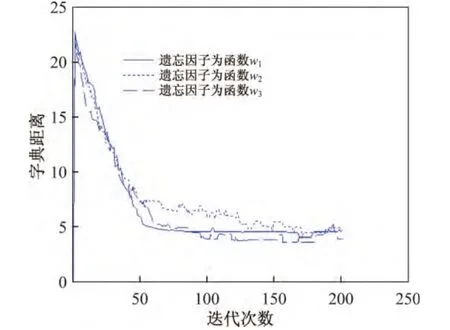
图8 字典距离随迭代次数的变化Figure 8 Dictionary distances of different number of iterations

由以上分析可以看出，遗忘因子取圆周函数w3时的字典学习总体衡量指标相对较好，字典学习效果更好，与真实字典更相似.

3.2.4 遗忘因子为逆退火阀值函数时的仿真结果

为了进一步研究RLS字典更新方法中遗忘因子对字典更新结果的影响，寻找合适的遗忘因子，取遗忘因子函数为不同逆退火阀值函数w1=1-(1-0.990)×(1-i/200)3、w2=1-0.08×0.5(i0.4)、w3=1-0.08×0.5(i0.3)、w4=1-0.04×0.8(i0.6)、w5=1-0.04×0.8(i0.5)、w6=1-0.04×0.8(i0.4)，并分析不同逆退火阀值函数字典更新的效果.

图9和10分别给出了不同逆退火阀值函数对应的分解误差以及字典距离随迭代次数的变化曲线.从图9和10中可以看出，遗忘因子取不同逆退火阀值函数对分解误差和字典距离的影响不大.表5列出了遗忘因子取不同逆退火阀值函数时对应的3种衡量指标.从表5中可以看出，不同逆退火阀值函数的运行时间略有差别；函数为w5时的字典相似性和总恢复比率较好，且运行时间为899.922 s，相对较小.由此可知，不同的逆退火阀值函数会对字典学习结果产生影响，但影响较小.

表4 不同圆周函数的指标结果Table 4 Results of the indicators of different cycle functions

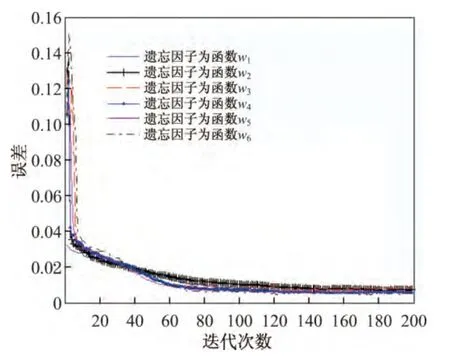
图9 分解误差随迭代次数的变化Figure 9 Decomposition errors variation with number of iterations

表5 遗忘因子为逆退火阀值函数时的指标结果Table 5 Results of the indicators with different annealing threshold functions of the forgetting factor

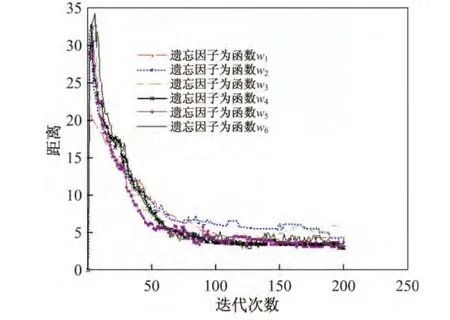
图10 字典距离随迭代次数的变化Figure 10 Dictionary distances of different number of iterations

4 结语

RLS字典学习方法与KSVD、MOD字典学习方法相比，学习字典与训练数据之间的相似性更强，更能反映训练数据的信息，减小了初始字典对学习字典的影响.在RLS方法中，当遗忘因子w在一定范围内取固定值时的字典学习效果较好，本文中的w为0.990时字典学习效果较好；遗忘因子为函数变量时的字典学习效果优于固定值时的字典学习效果.而对于不同的遗忘因子函数，当遗忘因子函数是曲率在一定范围内的圆周函数时，字典学习效果较好.当遗忘因子函数为逆退火阀值函数时，学习字典与遗忘因子为圆周函数时的学习字典之间的差别很小；同时，不同逆退火阀值函数对学习字典的结果影响较小.仿真结果与理论分析一致.

[1]焦李成，杨淑媛，刘芳，侯彪.压缩感知回顾与展望[J].电子学报，2011,39(7):1651-1662.JIAOLicheng,YANGShuyuan,LIUFang,HOU Biao.Development and prospect of compressive sensing[J].Acta Electronica Sinica,2011,39(7):1651-1662.(in Chinese)

[2]SKRETTING K,ENGAN K.Image compression using learned dictionariesby RLS-DLA and compared with K-SVD[C]//Proceedings of IEEE International Conferenceon Acoustics,Speech,Signal Process Pargue,Czech Republic,2011:1517-1520.

[3]ELADM.Sparse and redundant representations from theory to applications in signal and image processing[D].New York:Springer,2010.

[4]邓承志，曹汉强.多尺度脊波字典的构造及其在图像编码中的应用[J].中国图象图形学报，2009,14(7):1273-1278.DENG Chengzhi,CAO Hanqiang.Construction of multi-scale ridgelet dictionary and its application for imagecoding[J].China Journal of Image and Graphics,2009,14(7):1273-1278.(in Chinese)

[5]孙玉宝，肖亮，韦志辉，邵文泽.基于Gabor感知多成份字典的图像稀疏表示算法研究[J].自动化学报，2008,34(11):1379-1387.SUN Yubao,XIAO Liang,WEI Zhihui,SHAO Wenze.Sparse representations of images by a multicomponent Gabor perception dictionary[J].Acta Automatica Sinica,2008,34(11):1379-1387.(in Chinese)

[6]SHEN Bin,HU Wei,ZHANG Yimin,ZHANG Yujin.Image inpainting via sparse representation[C]//Proceedings IEEE International Conference on Acoustics,Speech,Signal Process.Taiwan,2009:697-700.

[7]刘金江，王春光，孙即祥.基于稀疏分解和神经网络的心电信号波形检测即识别[J].信号处理，2011,27(6):843-850.LIU Jinjiang,WANG Chunguang,SUN Jixiang.The detection and recognition of electrocardiogram's waveform based on sparse decomposition and neural network[J].Signal Processing,2011,27(6):843-850.(in Chinese)

[8]杨清山，郭成安，金明录.基于Gabor多通道加权优化与稀疏表征的人脸识别方法[J].电子与信息学报，2011,33(7):1618-1624.YANG Qingshan,GUO Cheng'an,JIN Minglu.Face recognition based on Gabor multi-channel weighted optimization and sparserepresentation[J].Journal of Electronics&Information Technology,2011,33(7):1618-1624.(in Chinese)

[9]彭富强，于德介，刘坚.一种基于多尺度线调频基的稀疏信号分解方法[J].振动工程学报，2010,23(3):333-338.PENG Fuqiang，YU Dejie，LIU Jian.Sparse signal decomposition method based on multi-scale chirplet[J].Journal of Vibration Engineering,2010,23(3):333-338.(in Chinese)

[10]SKRETTINGK,ENGANK.Recursiveleast squaresdictionary learning algorithm[J].IEEE Transactions on Signal Processing,2010,58(4):2121-2130.

[11]AHARON M,ELAD M,BRUCKSTEIN A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54(11):4311-4322.

[12]ENGANK,AASESO,HUSOYJ H.Method of optimal directions for frame design[C]//Proceedings IEEE International Conference on Acoustics,Speech,Signal Process,1999:2443-2446.

[13]JAFARIM G,PLUMBLEY M D.Fast dictionary learning for sparse representations of speech signals[J].IEEE Journal of Selected Topic in Signal Processing,2011,5(5):1025-1031.

[14]HYDER M M,MAHATA K.An improved smoothed l0approximation algorithm for sparse representation[J].IEEE Transactions on Signal Processing,2010,58(4):2194-2205.