一种求解二次模型信赖域子问题的新算法

朱帅, 李亮,, 王希云, 张雅琦, 于海波

(1.山西大同大学工学院, 山西 大同 037003; 2.太原科技大学应用科学学院, 山西 太原 030024)

一种求解二次模型信赖域子问题的新算法

朱帅1, 李亮1,2, 王希云2, 张雅琦2, 于海波2

(1.山西大同大学工学院, 山西 大同 037003; 2.太原科技大学应用科学学院, 山西 太原 030024)

在Hessian矩阵正定的前提下, 首先根据信赖域子问题精确求解方法的思想, 得到了最优曲线的参数方程, 进而建立了一种最优曲线的微分方程模型.针对此微分方程模型, 运用中点公式构造了一条折线.从而用该折线代替最优曲线, 提出了一种求解二次模型信赖域子问题的新算法.数值结果表明新算法比切线单折线法具有明显的优势.

最优曲线; 中点公式; 微分方程模型; 信赖域子问题

1 引言

在非线性优化中, 信赖域方法是一种被广泛应用而且具有全局收敛性的方法.信赖域方法的优点之一就是不要求目标函数是凸函数.

无约束最优化问题如下:

其中f (x):Rn→R 是目标函数,x∈Rn是待求变量.

当用信赖域方法求解(1.1)时, 关键在于每步迭代时都需求解下面形式的二次模型信赖域子问题:

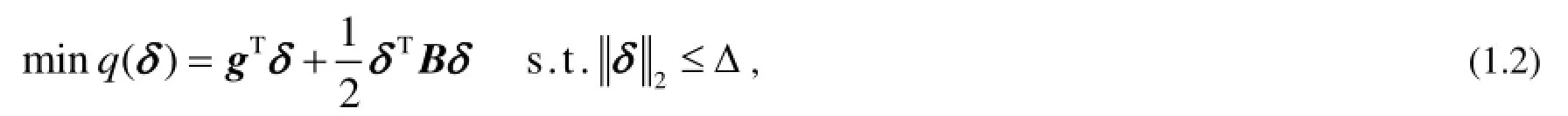
其中g∈Rn为目标函数在当前迭代点的梯度,B∈Rn×n为目标函数在当前迭代点的Hessian矩阵或其近似, Δ∈R 为信赖域半径,δ∈Rn为待求变量.当Δ变化时, 上述二次模型信赖域子问题(1.2)的解δ*形成一条空间曲线, 称为最优曲线[1].

如何求解二次模型信赖域子问题(1.2), 目前已经提出了很多方法[2-12].在 Hessian矩阵正定的情况下, 目前常用的折线法主要有单折线法、双折线法和切线单折线法[13-15].文献[15]的数值实验表明, 切线单折线法比单折线法、双折线法求解二次模型信赖域子问题(1.2)更有效.切线单折线法的思想: 连接点θ,δzp,δnp形成一条折线,称为切线单折线, 然后用该切线单折线近似最优曲线来求解二次模型信赖域子问题(1.2).其中θ是初始点, δnp=-B-1g,δzp是最优曲线在点δnp处的切线与-g 方向的交点.与其它折线法相比, 切线单折线法中所构造的折线则更近似最优曲线, 但是当信赖域半径小于时, 切线单折线法的数值结果是很不理想的.

折线法的基本思想就是寻找一条折线能够很好的近似最优曲线, 从而用该折线代替最优曲线来求解二次模型信赖域子问题(1.2).本文根据最优曲线的参数方程首先构造出了一个微分方程模型, 从而采用中点公式[16]构造一条折线X, 进而用折线X代替最优曲线来求解(1.2).数值结果表明新算法较切线单折线法具有很好的效果,尤其是信赖域半径小于时, 更显示了其明显的优越性.

2 微分方程模型的构造

定理2.1[17]δ*是子问题(1.2)的解, 当且仅当存在μ*≥0, 使得:

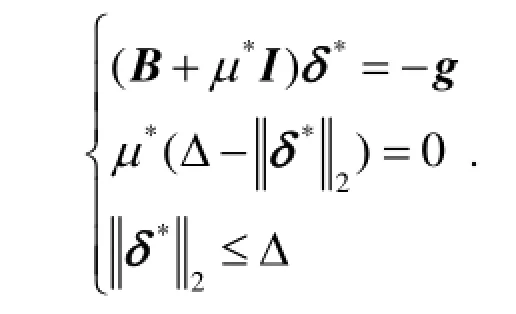
而且(B+μ*I)是半正定矩阵.

由定理2.1可知, 二次模型信赖域子问题的精确求解方法的思想即解下面的方程组:

当μ=0时, 二次模型信赖域子问题(1.2)的解δ*=-B-1g; 当μ＞0时, 则是通过求解一元非线性方程得到解μ*, 然后把μ*代入(2.1)的第一个方程, 则可以求出二次模型信赖域子问题(1.2)的解δ*=-(B+μ*I)-1g.

根据二次模型信赖域子问题的精确求解方法的思想, 则可以得到最优曲线的参数方程如下:

对参数方程(2.2)求导, 可得

对于微分方程(2.3), 借助求解微分方程的中点公式[16], 可构造一条折线X, 从而用该折线代替最优曲线来求解二次模型信赖域子问题(1.2).

3 构造折线X

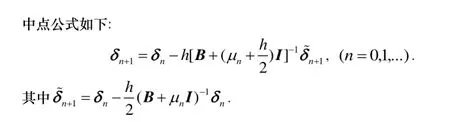
4 算法4.1

5 数值结果

对给定的测试函数1和测试函数2的信赖域子问题, 选取不同的信赖域半径Δ, 取步长0.5h=, 然后将算法4.1利用MATLAB进行了实验.并且用该算法求得的相关数据与切线单折线法求得的相关数据进行了比较.数值结果分别列在表1和表2中, 其中Δ表示信赖域半径,q表示测试函数的最优解的函数值,TDL表示切线单折线法,ZDL表示算法4.1,TDLZDLqq-表示使用切线单折线法与算法4.1所求得的测试函数的最优解的函数值之差, 该值越大, 表明算法4.1越好.测试函数见附录.

从表1和表2的数值结果可以看出, 对给定的不同的信赖域半径Δ, 都有TDLZDL0 qq-≥.故本文构造的折线X比切线单折线更好的近似了最优曲线.当信赖域半径(见文献[15])时, 算法4.1求得的测试函数的最优解比切线单折线法好很多; 当信赖域半径时, 算法4.1也稍好于切线单折线法; 当信赖域半径时, 算法4.1与切线单折线法所求得的测试函数的最优解相同.因此, 算法4.1是一个比切线单折线法更好的求解信赖域子问题的折线法.对于测试函数对于测试函数

表1 测试函数1的数值结果Tab.1 The numerical results of test function 1

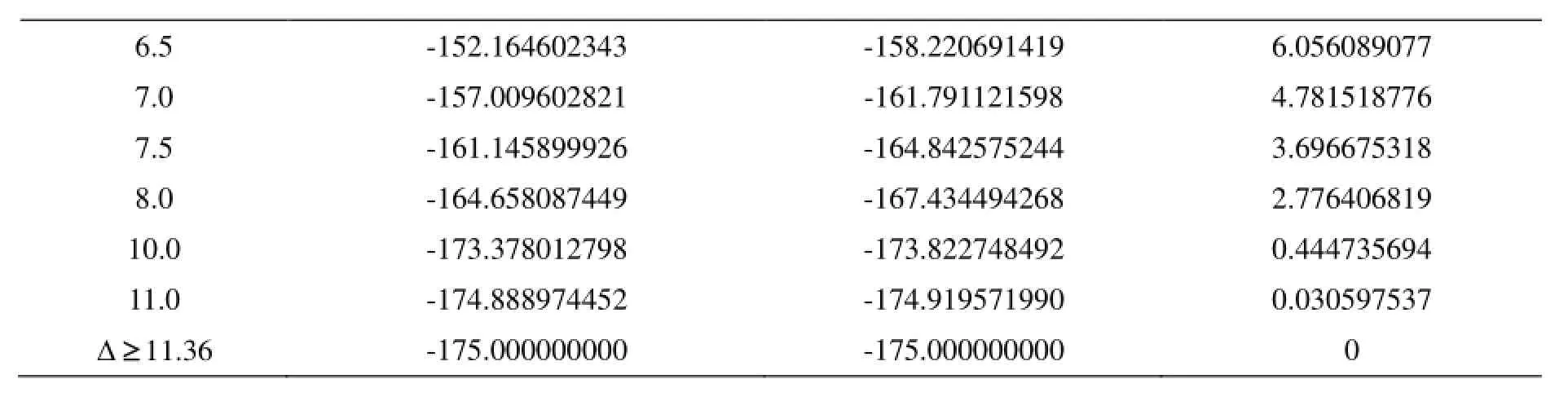
6.5 -152.164602343 -158.220691419 6.056089077 7.0 -157.009602821 -161.791121598 4.781518776 7.5 -161.145899926 -164.842575244 3.696675318 8.0 -164.658087449 -167.434494268 2.776406819 10.0 -173.378012798 -173.822748492 0.444735694 11.0 -174.888974452 -174.919571990 0.030597537Δ11.36≥ -175.000000000 -175.000000000 0

表2 测试函数2的数值结果Tab.2 The numerical results of test function 2

[1] 徐成贤,陈志平,李乃成. 近代优化方法[M].北京:科学出版社,2002.

[2] 赵英良,徐成贤.信赖域子问题使用重现开始策略的共轭梯度法[J].高校应用数学学报A辑, 2003,18(3):341-349.

[3] CHEN JUN, SUN WEN YU. Nonmonotone Adaptive Trust Region Algorithms with Indefinite Dogleg Path for Unconstrained Minimization[J]. Northeast Math J, 2008, 24(1): 19-30.

[4] 后刘生,孙文瑜.三项预处理共轭梯度法与信赖域子问题[J].南京师大学报: 自然科学版, 2001, 24(3): 1-6.

[5] WANG FU SHENG, WANG YAN PING. Nonmonotone Algorithm for Minimax. Optimization Problems[J]. Applied Mathematics and Computation, 2011, 217: 6296-6308.

[6] 赵丹.解信赖域子问题的混合折线法[J].徐州师范大学学报:自然科学版, 2009, 27(3): 38-41.

[7] ZHANG XIANG SUN, CHEN ZHONG WEN, ZHANG JU LIANG. A Self-adaptive Trust Region Method For Unconstrained Optimization[J]. Operation Research Transactions, 2001, 5(1): 53-62.

[8] 杨郁,王希云. 基于信赖域子问题的共轭梯度法[J]. 太原科技大学学报, 2010, 31(6): 481-484.

[9] 陈争,马昌风.求解信赖域子问题的一个光滑牛顿法[J]. 福建师范大学学报: 自然科学版, 2011, 27(4): 31-35.

[10] 吕立波. 解决大规模信赖域子问题的一种新算法[J]. 运筹与管理, 2007, 16 (5):48-52.

[11] PU DING GUO, HAN BO SHUN, YAO LIN, et al. A Class of Dogleg Trust Region Methods[J]. Operations Research Transactions, 2003, 7(1): 1-10.

[12] 张立, 唐志强. 解信赖域子问题的混合折线法[J]. 南京师大学报: 自然科学版, 2001, 24(1): 28-32.

[13] POWELL M J D. A Hybrid Method for Nonlinear Equations, Numerical Methods for Nolinear Algebraic Equations. P Rabinowtiz, Gordon and Breach, London, 1970.

[14] J E DENNIS JR, H H W MEI.Two New Unconstrained Optimization Algorithms Which Use Function and Gradient Values[J]. Journal of Optimization Theory and Applications, 1979, 28(4): 453-482.

[15] 赵英良, 徐成贤. 解信赖域子问题的切线单折线法[J]. 数值计算与计算机应用, 2000, 21(1): 77-80.

[16] 颜庆津. 数值分析[M]. 北京:北京航空航天大学出版社, 2006.

[17] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 2007.

A new algorithm for solving trust-region subproblems with quadratic model

ZHU Shuai1, LI Liang1,2, WANG Xi-yun2, ZHANG Ya-qi2, YU Hai-bo2(1. School of Technology, Shanxi Datong University, Datong 037003, P.R.C.;
2. School of Applied Science,Taiyuan University of Technology, Taiyuan 030024, P.R.C.)

On the premise that Hessian matrix is positive definite, first a parametric equation of the optimal curve is obtained according to the thought of the accurate method for solving trust-region subproblems. Then the paper establishes a differential equation model and constructs a broken line by midpoint formula. Meanwhile, a newt algorithm is presented by using the broken line instead of the optimal curve for solving trust-region subproblems. Numerical results indicate that the new algorithm has obvious advantage over the tangent single dogleg method.

optimal curve; midpoint formula; differential equation model; trust-region subproblem

O224

A

1003-4271(2014)01-0091-06

10.3969/j.issn.1003-4271.2014.01.19

2013-10-24

朱帅(1980-), 男, 讲师, 硕士, 研究方向: 最优化理论及其应用.

山西省自然科学基金(2008011013).