基于量纲分析的气力输送压降模型研究
2014-02-20王晓宁
张 妍,邢 婷,王晓宁
(辽宁石油化工大学, 辽宁 抚顺 113001)
基于量纲分析的气力输送压降模型研究
张 妍,邢 婷,王晓宁
(辽宁石油化工大学, 辽宁 抚顺 113001)
量纲分析法是建立数学计算模型的一种重要的方法。以实验室气力输送数据为基础,结合量纲分析法,建立了管道压降计算准数关联式,同时将计算结果与实验数据进行对比分析,实验值与计算值总体变化趋势基本相同,偏差较小,并对其中误差相对较大的公式进行了修正,所得准数关联式对化工气力输送中压降的估算具有实际意义。
气力输送;系统压降;量纲分析
量纲分析法又称为因次分析法,通过量纲分析,可以正确的分析各变量之间的关系,简化试验并对最后实验结果进行分析,所以量纲分析是我们分析流体运动的有力工具[1]。一些相关的文献是简单的管道中流体流动时而产生的压降,并不涉及气力输送过程中的发送压力和流量的影响[2],因此本文将对化工气力输送过程中压降利用量纲分析法进行求解。
1 实验概况
水平T型分支管路输送系统实验图,如图1所示。
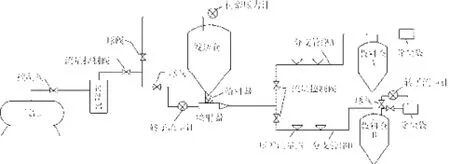
图1 水平T型分支管道实验图Fig.1 Figure level T branch pipe experiment
本试验的主输送管道为无缝钢管,管径是 32 mm,分支管长为 3 m,上面装有压力表和压差传感器。副输送系统通过T型分支接头连接主管路和两根分支管路而构成,采用球阀对两只分支管路A和B进行气固两相流的调节,得出压降的实验值。
2 量纲分析方法的理论基础
几个物理量的量纲彼此独立,即意味着表示它们的量纲矢量线性无关。量纲分析法的理论基础是“Π定理”:设某物理问题涉及n个物理量(包括物理常量) P1, P2, …,Pn, 而我们所选取的单位制中有m个基本量( n > m) ,则由此可组成n - m个量纲为1的量Π1,Π2,… ,Πn–m。若实际物理问题在物理量P1,P2,…,Pn之间存在物理定律(函数关系): f (P1, P2,…, Pn) = 0[3-5]。
3 准则方程的建立
化工气力输送流动过程中影响因素较多,其中流动过程中涉及影响系统压降的因素有8个,影响压降ΔPf的因素:管径d, 管长L, 流体密度ρ1,固体密度ρ2,流体粘度μ1,平均流速ub,管壁粗糙度ε,发送压力Ρ。化工气力压降模型 f(ΔPf,d, L, ρ1, ρ2,μ1, ub, ε, Ρ)=0[6]。
从上述 n=9个物理量中选出管径 d,平均速度ub,流体密度ρ1这3个物理量量纲是独立的,不能组成无量纲量。根据Π定理,则可得到其准则关系式 :f(π1,π2,π3.....π6)=0。
利用π定理及量纲分析法并经转化, 式中:k为无量纲变量,a1, a2, a3, a4, a5为待定指数。
4 方程的确定
因为分支管路A和B的流量是相同的,选择分支管路A为研究目标为了能更准确的确定方程, 可以对试验中流量数值为40,45 m3/h所得的具体数据进行分析,从而得到各个流量的压降方程:
流量Q=40 m3/h时,

流量Q=45 m3/h时,
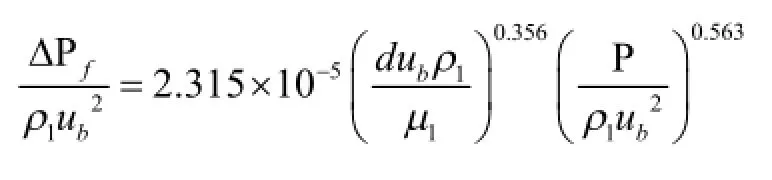
4 试验测试值与公式计算值的比较
(1)保持流量Q=40 m3/h不变,改变发送压力,实验值与计算值的比较见图1。

图1 流量40 m3/h时,压降随发送压力的变化Fig.1 The pressure drop along with the change of sending pressure when the gas flow is 40 m3/h
计算结果与试验值进行对比分析,发现整体趋势相同,相对误差在8.5% 左右,表明在该流量条件下该公式准确性较高。
(2)保持流量不变Q=45 m3/h,改变发送压力,实验值与计算值的比较见图2。
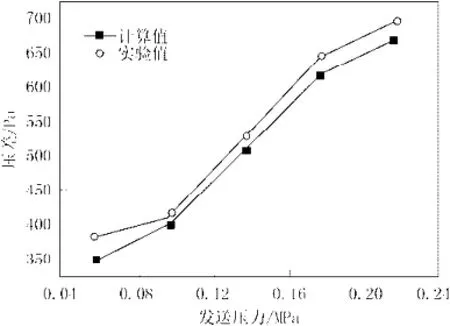
图2 流量45 m3/h时,压降随发送压力的变化Fig.2 The pressure drop along with the change of sending pressure when the gas flow is 45 m3/h
计算结果与试验值进行对比分析,发现相对误差相对较大,总体趋势大致相同,但在某个区间段的误差较大,可以对公式进行修正。修正后的公式:
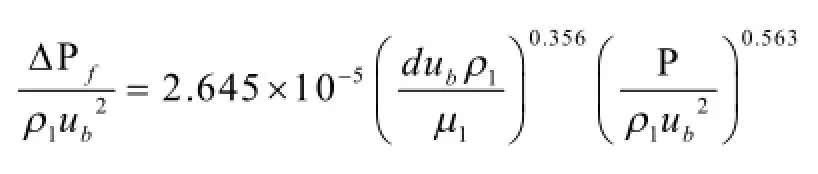
修正后的公式的计算值和实验值的相对误差不超过8.5%,见图3。
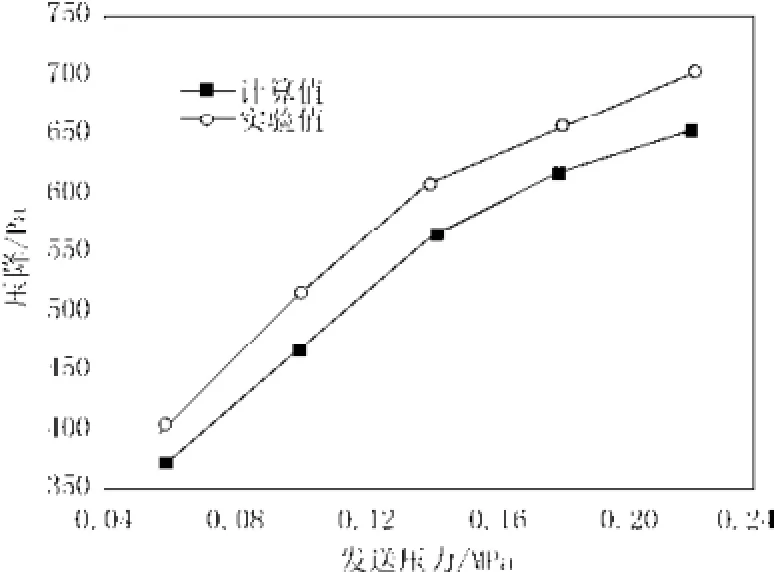
图3 修正后流量Q=45 m3/h时,压降随发送压力的变化Fig.3 The pressure drop along with the change of sending pressure when the gas flow is 45 m3/h after correction
表明公式经过修正后准确性较高。由图2与图3对比可知,随流量的增大,公式求解的相对误差较大,可能在流量增大的过程中,两相中气体与固体颗粒之间的摩擦以及颗粒与颗粒之间、颗粒与输送管道壁之间的碰撞频率会增加,在某个区间段存在误差,对公式进行修正后的公式相对误差变小。
(3)保持发送压力P=0.14 MPa, 改变流量,实验值与计算值的关系比较见图4。
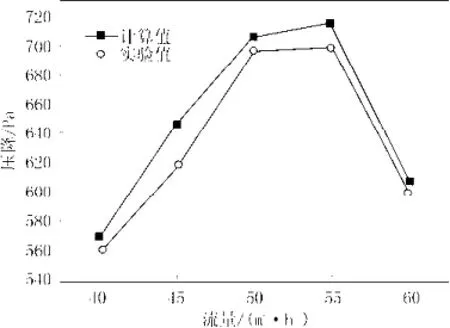
图4 发送压力0.14 MPa,压降随流量变化Fig.4 The pressure drop along with the change of the gas flow when the sending pressure is 0.14 MPa
由图4对比分析可知,在该发送压力条件下,计算值与实验值的相对误差在2.8%左右,相对误差在可以接受的范围内,表明在该发送压力条件下该公式准确性较高。
由图5可知,在该发送压力的条件下,计算值和实验值的相对误差较小,表明在该发送压力下公式的准确度较高,可以在工程上进行应用。
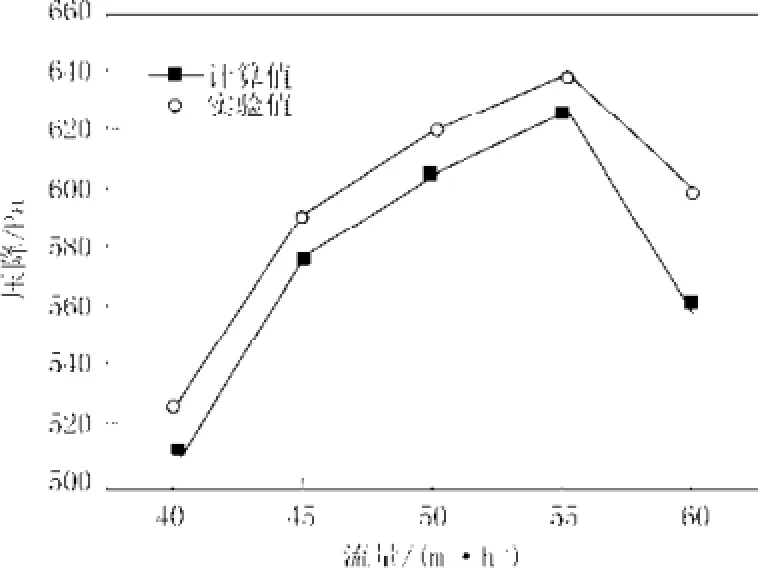
图5 发送压力0.22 MPa,压降随流量变化图Fig.5 The pressure drop along with the change of the gas flow when the sending pressure is 0.22 MPa
由上述分析可知发送压力和流量都是影响压降的因素,但是利用量纲分析法求解的压降计算公式求解计算值时,在某种程度上保持流量不变的情况下,改变发送压力求解的计算值的相对误差较大,必须对公式进行修正才能估算压降的数值。
5 结 论
(1)本文是在实验室数据的基础上,结合量纲分析法,建立了的管道系统压降计算准数关联式,并对计算值与实验数据进行了对比分析。
(2)用量纲分析法求解压降的计算值与实验值的总体趋势相同,偏差较小,对化工气力输送压降计算有一定的实际意义。
(3)在用量纲分析法求解压降计算值时,对于部分相对误差较大的公式进行修正,修正后的公式基本能满足要求,说明量纲分析法建立准数关联式求解压降的方法是可行的。
[1]杨振起.量纲分析及其应用[J].济南交通高等专科学校学报,2010(3):27-30.
[2]Lu Haifeng,Guo Xiaolei,Huang Wanjie,etal.Flow characteristics and pressure drop across the Laval nozzle in dense phase pneumatic conveying of the pulverized coal[J]. Chemical Engineering and Processing, 2011( 50) : 702-708.
[3]STIMLER FJ.Demonstration of procedure for desining impact bag attenuation systems with predictable performance[J]. Aircraft, 2010 , 14(5): 502-507.
[4]宋德政. 量纲分析原理及应用[J]. 西南工学院学报, 1999, 14(2): 75-79.
[5]王新颖,邵辉,王宏鑫. 基于量纲分析的输液管道泄漏量计算模型研究[J]. 江苏工业学院学报,2010, 36(4): 43-44.
[6]朱荣杰,唐莉, 等. 基于量纲分析法求抽油泵柱塞的下行阻力[J].北京:石油工业出版社, 2009(1): 23-25.
Research on the Pneumatic Conveying Pressure Drop Model Based on Dimensional Analysis
ZHANG Yan,XING Ting,WANG Xiao-ning
(Liaoning Shihua University, Liaoning Fushun 113001,China)
Dimensional analysis is a kind of important method to establish mathematical models. In this paper, based on laboratory data, combined with the dimensional method, a relatively simple calculation formula of the pipeline system pressure drop was established. At the same time, the experimental values and calculated values were compared and analyzed. The results show that, the deviation of calculated values is small; after the formula to cause relatively large errors is revised, it has a certain practical significance in estimating the chemical pneumatic conveying pressure drop.
pneumatic conveying; mathematical model; dimensional analysis
TQ 022.3; TH 232
A
1671-0460(2014)11-2454-03
2014-04-15
张妍(1989-),女,吉林白山人,在读硕士,研究方向:石油化工节能技术。E-mail:zhangyan19890304@163.com。
王晓宁(1972-),男,副教授,博士,研究方向。E-mail:wxning333@163.com。
