基于模糊解耦控制的车辆转向制动系统研究

陈燕芹，李晓旭，段婷婷

（1.长安大学汽车学院，陕西 西安 710054；2.南京航空航天大学车辆工程系，江苏 南京 210016）

基于模糊解耦控制的车辆转向制动系统研究

陈燕芹1，李晓旭1，段婷婷2

（1.长安大学汽车学院，陕西 西安 710054；2.南京航空航天大学车辆工程系，江苏 南京 210016）

车辆转向系统和制动系统之间存在着很强的速度耦合关系，造成两个系统之间的性能相互影响，使得车辆在转向制动这一工况成了汽车最危险的工况之一。本文结合实际车辆参数建立转向系统的二自由度模型和制动系统的单车轮模型，针对车辆转向制动工况设计了模糊解耦控制器，实现了车辆的转向与制动同时控制。经验证含有模糊解耦控制的车辆转向制动系统具有很好的动态控制效果，并且有很强的鲁棒性和自适应性。

车辆转向制动；模糊解耦控制；Matlab仿真

CLC NO.: U461.2 Document Code: A Article ID: 1671-7988(2014)09-19-04

引言

近年来随着汽车技术和汽车制造业的快速发展和汽车拥有量的快速增加，交通状况更加错综复杂、交通事故频发。因此，人们对汽车行驶的安全性、操纵性以及舒适性的要求也逐渐提高。这种趋势促使现代电子控制技术被广泛地应用在汽车上，例如较成熟的有防抱死制动系统（ABS）、主动前轮转向系统（AFS）、驱动力控制系统（TCS）、四轮转向系统（4WS）、主动悬架系统（ASS）以及电子稳定控制系统（ESP）等[1]。随着研究的深入，我们逐渐认识到汽车是一个复杂的有机整体，仅仅研究车辆的某一项性能并不能提高其整体性能，整车性能的提高依赖于所有子系统的相互协作。

在汽车行驶过程中，转向制动是一种常见工况，是衡量汽车安全性和操纵稳定性的重要指标。如果驾驶人在车辆转弯行驶过程中采取制动措施，纵向力与侧向力会同时施加在轮胎上，若所受的纵向力被摩擦力抵消，车轮所受到的侧向力也会消失，这时车辆在横向上就失去了抗干扰能力，此时若前轮先抱死，则车辆失去转向能力，无法遵循弯道行驶，在有限宽度的车道上容易偏出车道；若后轮先抱死，则车辆在偏向风、路面坡度的干扰下，后轮发生侧滑、甩尾等造成交通事故，使得操纵稳定性恶化[2-3]。本文针对车辆的转向系统和制动系统设计控制器，该控制器采用模糊解耦算法实现车辆转向/制动系统的同时控制，使车辆在转向制动工况下获

得良好的稳定性和操纵性。

1、车辆制动系统和转向系统模型的建立

1.1 车辆转向系统模型的建立

在模型建立过程中，本文将悬架与转向系的侧倾转向角、侧向力转向角、轮胎侧偏角一起看作前后轮的综合侧偏角，这样可将车辆近似为二自由度系统来分析以转向角δ（折算到前轮处）输入时车辆的反应。特别是在转向时可以满足车辆的横向稳定性设计的要求。作为基本分析，略去空气阻力影响，建立Y向力平衡与绕重心的力矩平衡，其二自由度模型[4]如下：

整理得系统的状态方程为：

1.2 车辆制动系统模型建立

由于车辆制动系统在实际工况下是非常复杂的，因此本文在建立车辆制动系统模型的过程中忽略了一些不确定因素的影响，这样可以简化研究。制动系统模型建立在二自由度的基础上，主要分为两个子系统：一是车辆车轮动力学模型，二是滑移率和附着系数μ-λ模型。两个子系统联合构成了汽车制动系统的整体，其中控制目标是控制滑移率λ为期望值，控制量是做用在每个车轮上的制动力矩或力[4]。

1.2.1 车辆动力学模型

本文选用的车辆动力学模型为单轮车辆模型，该模型主要描述车辆的制动性能，可以减少干扰，简化问题。另外在使用单车轮模型时，忽略纵向惯性力对车轮造成的附加垂直负载和道路状况对制动系统造成的干扰和影响，做出如下假设：车轮抱死的过程时间很短；车轮负载为常数，等于车轮与地面之间的压力；不考虑风阻力和轮胎滚动阻力；不考虑车轮横向力的作用，切纵向附着系数曲线分段线性化。单车轮模型制动时受力分析[5]，如图1所示。

基于以上假设建立汽车动态学方程：

式中：m汽车质量，kg；v车辆速度，m/s；Fb汽车附着力，N；I车轮转动惯量，kg·m2；R车轮半径，m；ω车轮角速度，rad/s；μ车路与地面的附着系数；N车轮对地面的法相反力，N；Tb制动力矩，N*m。

1.2.2 滑移率和附着系数μ-λ模型

根据滑移率的相关研究成果，其可定义为：

其中，λ为车轮滑移率；R为车轮半径，m；v为汽车速度，m/s；w为车轮角速度，rad/s；

从式7（即滑移率定义）中可知，当汽车速度等于车轮速度时，滑移率为0，即此时车轮处于自由滚动状态，车辆没有制动。车轮受到制动力时，车轮速度减小，滑移率开始增大，当滑移率达到100%（即车轮速度为零）时，车轮即达到了抱死状态[6]。此时车辆的操纵性大大降低，处于失控状态，这是我们必须要避免的。

由（7）公式进行微分运算得：

由上式可以看出，车辆的制动系统和转向系统均受到车速的影响，两个系统存在很强的耦合性。

1.2.3 单车轮轮胎模型

经研究发现当滑移率处于一个固定值附近时地面摩擦力达到最大，此时车辆达到最佳制动条件。本文选用双线性轮胎模型来简化轮胎模型，附着系数与滑移率的关系如下图2所示。

由图中曲线可知滑移率和附着系数的数学模型为：

式中：λT最佳滑移率；λ滑移率；μg滑移率为100%的纵向附着系数；μh峰值纵向附着系数；μb纵向附着系。

由图2可知，当滑移率保持在10%-30%时，车辆滑移率维持在峰值附着系数附近，此时地面摩擦力保持最大值，车轮处于边滚边换状态，纵向附着力和侧向附力也能达到最大值，可以在传递最大制动力的同时保持侧向稳定性。在设计车辆防抱死制动系统时，车辆将不断调节制动力矩大小，保证车轮的滑移率最佳（假设为20%左右），这样不但可以防止车轮抱死，获得最大制动力，也可以保持车辆转向时的侧向稳定性。

2、基于模糊解耦控制的转向制动系统

2.1 转向制动系统的模糊解耦控制原理

转向制动这一工况存在危险性，这是因为车辆在转向过程中如果紧急制动，由于速度变化，使得制动性能大大下降，甚至失去控制或者甩尾，因此要想得到理想的转向和制动性能需要将由于速度变化对转向性能产生的影响降到最低或者消除。针对非线性时变系统的转向系统模型和制动系统模型，本文选用模糊解耦控制的方法[7-9]。

模糊解耦控制利用模糊控制规则实现对被控量的解耦，从而实现网络补偿。将耦合回路的控制量定为主回路的干扰输入，通过模糊解耦控制器的输出对控制量进行补偿，来抵消回路中的耦合作用。最终使得一个控制量只影响一个单一的控制系统，实现解耦。模糊解耦控制器是模糊解耦控制系统的核心，因此模糊解耦控制器的设计以及调校是影响整个系统能否成功的关键性因素[10-11]。本文采用二位模糊控制器，并采用直接解耦的方法，具体实现是，根据人工操作的经验，构建一定的模糊规则，被控对象的控制量作为控制器的输入，用控制器的输出对被控对象进行补偿，系统的结构框如图3所示。

其中，车辆转向系统和制动系统的控制量U1，U2和输出量的微分量y1，y2作为模糊解耦控制器的输入。解耦控制的输出量ΔY1，ΔY2分别作为转向系统和制动系统的补偿量。W1=U1+ΔY1，W2=U2+ΔY2为被控对象的输入量[12]。

2.2 模糊解耦控制的车辆转向系统仿真

针对本文中二自由度的转向系统，在进行仿真时，车辆选用参数如表1所示。

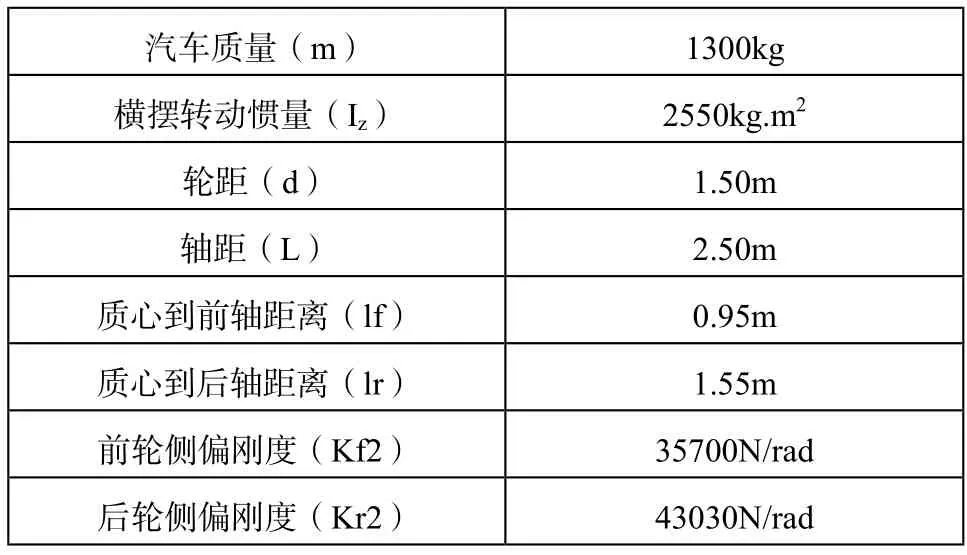
表1 汽车横向运动模型参数

转向系统的仿真原理：为了保证转向系统有较好性能，必须保证转向系统的输出量，即车辆的横摆角速度需要保持一个定值（即匀速转向），这样不仅可以保证转向时的稳定性，还能获得较好的转向速度（通常保持在2.5rad/s）。加入模糊解耦控制器后的转向系统仿真图，如图4所示。

由图4可知，经过模糊解耦控制的补偿作用后，整个转向系统的控制效果较好，延迟时间短，超调量较低，在一定程度上可以满足需求，转向稳定性较好。

2.3 模糊解耦控制的车辆制动系统仿真

针对本文中的单轮防抱死制动模型，在进行仿真时，车辆选用参数如表2所示。

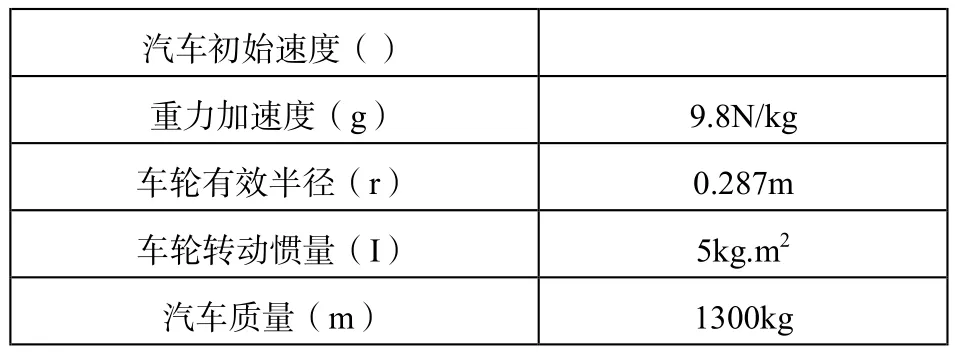
表2 汽车纵向运动模型参数

制动系统的制动原理：控制系统的输入量为滑移率的给定值（期望的最优滑移率，一般为0.2）和实际滑移率的差值，通过模糊解耦控制的调节作用使滑移率始终在给定值附近。这样不仅可以获得最大制动力，也能获得最好的制动效果，应用模糊解耦控制的单轮防抱死制动模型仿真图，如图5所示。

由图5可知，滑移率在1s时候就已经达到了期望值，并且一直维持在期望值上，仿真结果中没有超调量的存在，对于车轮速度和车身速度的仿真图可以看出，车速下降的更加平稳，可见模糊解耦控制的使得车辆具有较好的制动性。

3、结论

本文研究了目前常用的车辆转向系统和制动系统的结构，建立了车辆转向系统模型和制动系统的数学模型。其中转向系统采用的是二自由度的模型，这样不仅简化了研究难度，还能重点体现出转向性能；制动系统中轮胎模型采用的是便于数学表达的双线性模型，而车辆模型采用的是更能体现制动性的单轮模型。

在建立数学模型的基础上，介绍了模糊解耦控制原理，然后在Matlab/Simulink环境中，以防抱死制动系统和主动前轮转向系统为基础，分别对模糊解耦控制的车辆转向制动同时控制系统进行了仿真试验，仿真结构表明模糊解耦控制抗干扰能力、很强的鲁棒性，在其控制下的车辆具有较好的转向制动性。

[1] 王霞.汽车防抱死制动与主动前轮转向系统[D].合肥:合肥工业大学,2007.

[2] 李果,刘华伟,王旭.汽车转向/防抱死制动同时控制[J].控制理论与应用,2010,27(12): 1699-1704.

[3] 冯泽斌.汽车转向制动的协同控制研究[D].北京:北京科技大学,2008.

[4] 郭孔辉.汽车操纵动力学原理[M].江苏:江苏科学技术出版社,2011.

[5] 李君,喻凡,张建武等.汽车转向制动防抱死系统仿真研究[J].系统仿真学报，2001,13(6): 789-793.

[6] 叶磊,尹作发.基于Matlab/Simulink的车辆制动过程分析[J].公路与汽运,2006,117:5-7.

[7] 张国立,张辉,孔倩.模糊数学基础及应用[M].北京:化学社,2011.09.

[8] 玉清,唐永哲,郝涛.自适应解耦控制方法的研究[J].弹箭与制导学报,2008,06:41-43.

[9] 柴天佑.多变量间接自适应解耦控制算法[J].自动化学报.1991,17 (5):51-54.

[10] 李果,彭莎.汽车转向/制动系统的非线性解耦内模控制[J].系统仿真学报,2012,24 (8): 1714-1718.

[11] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.

[12] 张代胜,顾勤林,陈朝阳等.车辆转弯制动防抱死系统仿真[J].农业机械学报,2005,36(9): 16-20.

Research of vehicle steering and braking system based on fuzzy decoupling control

Chen Yanqin1, Li Xiaoxu1, Duan Tingting2
（1.School of Automobile, Chang’an University, Shaanxi Xi’an 710054; 2. Department of Automotive Engineering, Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing 210016）

The strong velocity coupling relationships between the automotive steering and braking systems and the systems' performance of mutual influence make the vehicle steering and braking working condition become one of the most dangerous conditions. This paper established a two degree of freedom model of automobile steering systems and a single wheel braking system model based on the actual parameters of vehicle, and designed the fuzzy decoupling controller for controlling simultaneously vehicle steering and braking systems. As a result, the fuzzy decoupling controller of vehicle steering and braking systems has good dynamic control effect, and has strong robustness and adaptability.

vehicle steering and braking; fuzzy decoupling; Matlab simulation

U461.2

A

1671-7988(2014)09-19-04

陈燕芹，硕士研究生，就读于长安大学汽车学院车辆工程专业。