基于灰色系统模型的西安市客运量预测

苏薇，张艳，李亚林，曹文娟

（长安大学 汽车学院，陕西 西安 710064）

基于灰色系统模型的西安市客运量预测

苏薇，张艳，李亚林，曹文娟

（长安大学 汽车学院，陕西 西安 710064）

根据西安市近几年的客运情况，运用灰色系统模型理论建立GM（1，1）模型。通过检验，得出所建模型预测精度高，适用于西安市客运量预测。运用此模型得到客运量预测数据。

灰色系统模型；GM（1，1）；检验；客运量预测

CLC NO.: [U-9] Document Code: A Article ID: 1671-7988(2014)09-07-03

引言

客运量是评价运输组织效果的指标，是衡量旅客运输生产劳动量的尺度，是统计期内运送的旅客数量。客运量实质上体现了运输部门的绝对成果，体现了运输组织方式满足社会需要程度的大小[1]，也是制定和检查运输生产计划、研究运输发展规模和速度的重要指标。对西安市交通客运量及其发展趋势进行预测与分析，可以有效地规划和组织西安市旅客运输，为西安市交通运输规划提供决策的理论依据，提高交通运输经济效益和社会效益，为建设西北国际化大城市提供重要的交通支持。

客运量预测早期使用的方法有指数平滑法、回归分析法、马尔可夫分析法、弹性系数法、增长率统计等方法［2］。由于线性回归分析法需要搜集大量的信息，计算工作量大，建模困难，不利于预测的实现。而指数平滑法等时间序列法的预测精度不高[3]。灰色系统预测具有要求样本数据少、原理简单、运算方便、短期预测精度高、可检验等优点。因此，针对客运量这样一个受到多层次、多因素影响的复杂变量，为了消除不确定因素的影响，提高预测精度，本文采用灰色系统模型对西安市客运量进行预测。

1、灰色预测模型GM（1，1）基本原理

灰色系统理论是我国学者邓聚龙教授在1982年创立的，灰色系统是指元素信息不完全、结构信息不完全、关系信息不完全、运行行为信息不完全的系统[4]。它的研究对象是不确定性系统，通过对少量数据建立微分方程模型，对已知信息进行生成、开发和提取，实现对系统运行行为、演化规律的正确描述和有效监控。灰色系统理论研究的内容有系统分析、信息处理、灰色建模、灰色预测与决策、灰色控制、灰色聚类与灰色统计等。本文采用灰色预测模型对西安市客运量进行预测，有效的避开了需要信息量大、建模困难、计算工作量大这些问题，强调从已存在的灰色信息里找出系统的内在规律，进而使模型简单化、明确化。

1.1 生成时间序列

GM（1，1）预测模型是灰色预测模型中最常用的一种，本文采用该模型对西安市客运量进行预测。已知原始时间序列，为了减弱它的随机性，先要对原始序列进行数据处理，即通过累加的方式产生时间序列。

原始时间序列：

由于生成序列接近指数曲线，可认为是光滑的离散系数，则可用微分方程进行描述。

1.2 灰色预测模型GM(1，1)的建立

对于上述生成的时间序列，GM(1，1)相应的微分方程为

求解微分方程，即可得到预测模型如下：

在上式中，参数a，b的值使用最小二乘法进行估计，式中：a为发展系数，其大小反映了原始序列的增长速度；b为灰作用量。令

1.3 灰色预测模型GM(1,1)精度检验

对于已建立的模型是否可靠，需要经过残差检验和后验差检验，只有通过检验且精度合理的模型才能成功的进行预测，否则需要进行残差修正。其中，模型精度检验标准如下表1[5]所示。

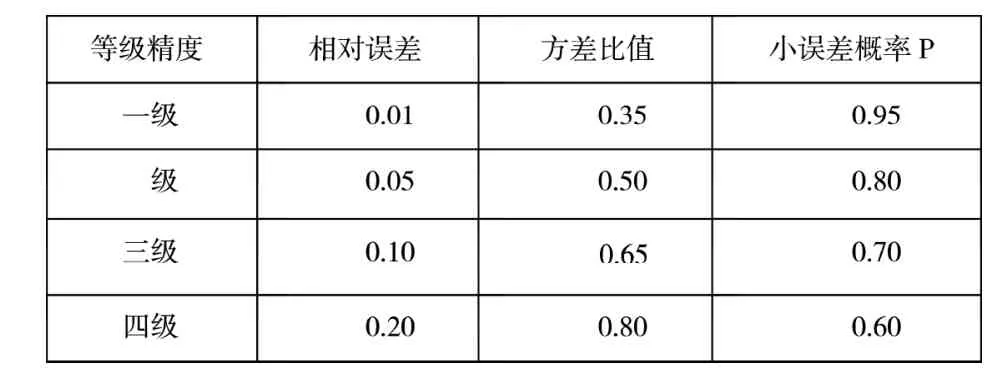
表1 模型精度检验标准

进行精度检验的方法如下

（1）残差检验

计算原始序列和原始数列的灰色预测数列之间的绝对误差及相对误差：

2、用灰色预测模型GM(1,1)对西安市客运量进行预测

本文选择2009年至2013年西安市客运量数据建立模型，用灰色系统预测理论对西安市今后几年的客运量进行预测研究。

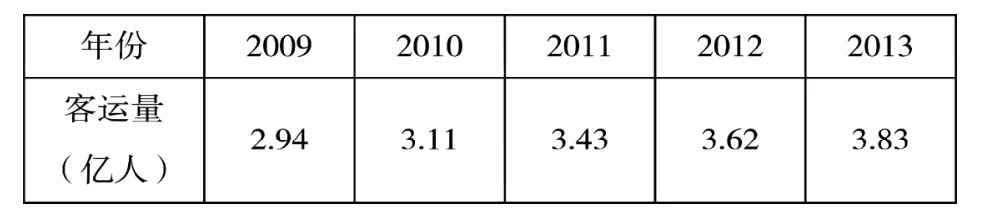
表2 西安市2009～2013年旅客运输量

西安地处中国陆地版图中心和我国中西部两大经济区域的结合部，是西北通往中原、华北和华东各城市的必经之路，具有承东启西、连接南北的重要战略地位，因此，对西安市的客运量做出正确的预测能更好的促进西部地区的政治、经济和文化发展。在灰色系统模型中，以2009年为基年来进行预测。

已知原始生成序列为：

对其进行一次累加生成序列：

对生成的时间序列，GM(1，1)相应的微分方程为：

构造数据矩阵B和数据向量Yn，把数据直接带入公式可得：

把所构造的数据矩阵和数据数量代入公式，用最小二乘法，解出微分方程中的参数a，b。

可知a=-0.0667，b=2.8546

代入可得出微分方程为：

故可以得出预测模型为：

灰色系统模型的检验（1）残差检验

绝对残差序列：

相对残差序列：

对照表1得出预测模型精度等级为一级，所建立的模型不需要进行残差修正。

（2）后验差检验

小误差概率p=1，模型预测精度等级为一级。

通过以上残差检验、关联度检验和后验差检验可知，所建立模型的预测精度等级为一级，预测精度很高，因此可以用所建立的模型对西安市未来几年客运量进行预测。运用模型得到西安市2014～2018年客运量的预测结果见表2：

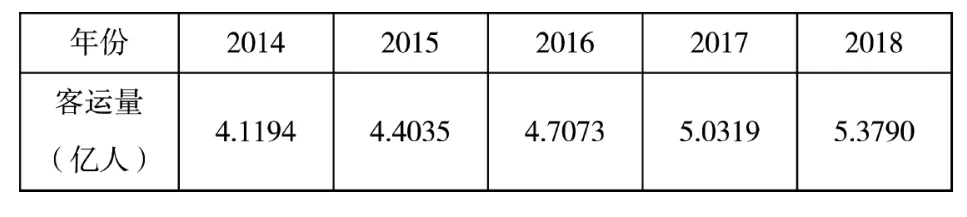
表3 西安市2014-2018年客运量预测值

为更直观的体现西安市客运量的变化情况，对表3所得预测数据和实际已知数据进行对比可得下图1。

通过图1中客运量预测值和实际值进行对比分析可以看出2009年到2013年预测值和实际值拟合效果较好，预测值与实际值相差不大，从而进一步验证了模型预测的精度高的结论。

从图1可以直观的看出西安市客运量以后几年将持续增长，且增长趋势平稳。

通过预测可知，2018年西安市客运量预计达到5.379亿人，而2009年客运量仅为2.94亿人，前者接近于后者的两倍，由此可以看出西安市未来几年客运量总体增幅较大。

3、结论

（1）基于灰色系统模型的灰色预测方法可以很好地克服数据信息的不完善，在现有小量数据的基础上进行模型的建立，强调从系统存在的灰色信息里找出系统的内在规律，进而使系统明确化，化复杂为简单，化模糊为清晰。

（2）通过灰色系统模型对西安市客运量进行预测，通过预测值与实际值对比，得出预测精度高的结论，可以为西安市客运量预测提供一个可行的预测模型，从而为西安市规划和组织旅客运输提供有力的理论依据。

（3）本文采用的数据相对简单，若数据较为复杂的话，采用此种预测模型计算过程相对复杂，采用相关预测软件如Matlab等可使预测过程较为简便，预测结果的可靠性较高。

[1] 霍娅敏，李德刚.成都市公路客运量预测[J].交通标准化.2005.

[2] 蔡家明. 基于灰色系统模型的公路客运量预测研究[J].上海工程技术大学学报.2003.

[3] 刘长虹，黄虎，陈力华.客运量预测方法的探讨[J].上海工程技术大学学报.2004.

[4] 邓聚龙.灰色控制系统[M].武汉:华中理工大学出版社,1993.

[5] 张永杰. 基于灰色系统理论客运量和客运周转量的预测[J].山东交通学院学报.2003.

The Passenger Traffic Forecast Of Xi’an Based On Grey System Model

Su Wei, Zhang Yan, Li Yalin, Cao Wenjuan
(College of Automobile Chang’an University, Shaanxi Xi’an 710064)

According to xi 'an passenger transport situation in recent years,and making use of the theory of grey system model to establishe GM (1, 1) model . The conclusion is that the model prediction accuracy is high through the test,and it’s suitable for xi 'an passenger traffic forecast.We get the passenger traffic forecast data by using the model.

grey system model; GM（1，1）; test; passenger traffic forecas

[U-9]

A

1671-7988(2014)09-07-03

苏薇，长安大学汽车学院硕士研究生，就读于载运工具运用工程专业。