建立在泊松方程上的空间电荷密度测量技术

程文锋 汪振

摘 要：本论文以泊松方程的基本公式为中心，通过数学转换和物理建模，巧妙地解决了泊松方程的边界条件问题，直接求取了空间电荷密度与电场的关系式。本论文还根据基本的物理学知识对传感器进行了设计，实现了空间静电场转化为电流信号功能，进而转化为电压信号，其功能上还能辨识电荷极性。最后通过物理模型的电场分布特性计算了如何通过直流电场对测量装置进行校正。本论文所设计的空间电荷密度测量技术可应用于大气电荷研究、电荷移动研究等。

关键词：泊松方程；电荷密度；电极；电场强度；

中图分类号：TH762 文献标识码：A

目前测量空间电荷密度多采取的是间接方式，如声波、激光、热脉冲等。这些方法受环境影响较大，精度不高，同时也容易影响被测电荷。本论文所提出的测试方法是建立在最基本的物理方程上进行展开，通过公式推导和巧妙的设计，实现对空间电荷密度的测量。

1 测量装置的基本原理

物理学中的泊松方程的微分形式为▽2=-ρ/ε，其中ρ代表电荷密度，它在空间上是一个三维方程。若只考虑x方向的泊松方程，则有式（1）。

（1）

图1为测量装置的物理模型，模型的上、下电极通过侧壁连接，它们之间的距离为d。设装置里面充满了电荷密度为ρ的电荷，同时在它的作用下，在上、下电极上形成电压U0。模型的下电极上装有静电式电场传感器。图1模型中还建立了x轴坐标，其方向以下电极的表面为起点，向上电极方向为正。所建立的物理模型在x方向上的电场只与电荷ρ有关，与外电场无关，即两端电极上只有装置空间的电荷作用，与外电场无关。

解方程（1）得式（2）。

（2）

式（2）等式的du/dx即为上、下电极间的电场强度。对式（2）求解得式电极间的电压表达式（3）。

（3）

在边界条件x=0，电压u=U0；x=d，电压u=U0时，求得

，c2=U0，将

代入式（2）得两端间的电场强度Ex。

（4）

当x=0时，；当x=d时，

当x=d/2时，Ed/2=0。

通过上面分析，在x=0处存在空间电荷密度与电极表面的电场强度有直接的线性关系，即

所以只要通过传感器测量出E0，就可通过计算求出空间电荷密度ρ。

2 传感器设计

静电传感器的设计原理模型是基本上是在静电场中放置一个导体，导体表面就会产生感应电荷，当电场变化时感应电荷也变化，使导体内部电荷的移动形成微弱电流。根据微弱电流的变化或电荷移动所产生的效应，就可知电场的变化。但在实际测量中，传感器所在的静电场中电场基本不变或缓变，不易测量所处在静电场的变化。

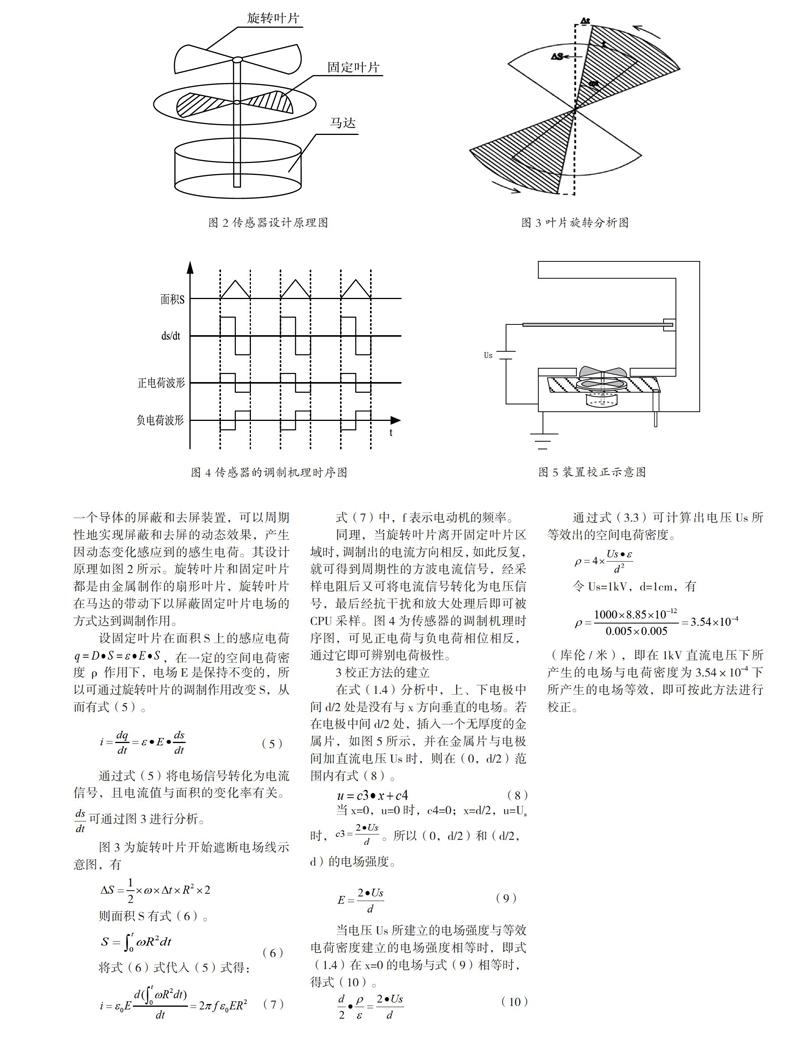
该传感器的设计方法采用静电式场强测量方式，采用遮挡片遮挡的形式对一个导体的屏蔽和去屏装置，可以周期性地实现屏蔽和去屏的动态效果，产生因动态变化感应到的感生电荷。其设计原理如图2所示。旋转叶片和固定叶片都是由金属制作的扇形叶片，旋转叶片在马达的带动下以屏蔽固定叶片电场的方式达到调制作用。

设固定叶片在面积S上的感应电荷，在一定的空间电荷密度ρ作用下，电场E是保持不变的，所以可通过旋转叶片的调制作用改变S，从而有式（5）。

（5）

通过式（5）将电场信号转化为电流信号，且电流值与面积的变化率有关。可通过图3进行分析。

图3为旋转叶片开始遮断电场线示意图，有

则面积S有式（6）。

（6）

将式（6）式代入（5）式得：

（7）

式（7）中，f表示电动机的频率。

同理，当旋转叶片离开固定叶片区域时，调制出的电流方向相反，如此反复，就可得到周期性的方波电流信号，经采样电阻后又可将电流信号转化为电压信号，最后经抗干扰和放大处理后即可被CPU采样。图4为传感器的调制机理时序图，可见正电荷与负电荷相位相反，通过它即可辨别电荷极性。

3 校正方法的建立

在式（1.4）分析中，上、下电极中间d/2处是没有与x方向垂直的电场。若在电极中间d/2处，插入一个无厚度的金属片，如图5所示，并在金属片与电极间加直流电压Us时，则在（0，d/2）范围内有式（8）。

（8）

当x=0，u=0时，c4=0；x=d/2，u=Us时，。所以（0，d/2）和（d/2，d）的电场强度。

（9）

当电压Us所建立的电场强度与等效电荷密度建立的电场强度相等时，即式（1.4）在x=0的电场与式（9）相等时，得式（10）。

（10）

通过式（3.3）可计算出电压Us所等效出的空间电荷密度。

令Us=1kV，d=1cm，有

（库伦/米），即在1kV直流电压下所产生的电场与电荷密度为3.54×10-4下所产生的电场等效，即可按此方法进行校正。

结语

通过泊松方程基本公式的简单求解，并结合物理模型的巧妙设计，解决了泊松方程边界条件，还得到了空间电荷密度与电场的线性关系。然后通过静电式传感器的设计将电场调制成电流信号，再经采样处理后即可被CPU读到。最后还介绍了如何利用直流电场对装置进行校正的原理和方法。

参考文献

[1]刘志远，姜晶，赵佳龙，等.小型振动电容式静电传感器的设计[J].仪表技术与传感器，2011（11）.