高斯平面工程控制网坐标系统的选择

张洪波，李志伟， 赵 岚

（1. 武汉大学 测绘学院，湖北 武汉 430079；2. 中工武大设计研究有限公司，湖北 武汉 430072）

将地球不规则表面上的控制点归算到平面上从而建立平面坐标控制系统，必须进行投影。投影的方式很多，我国统一采用的是高斯-格吕格投影。此类投影的特点是无角度变形，但其边长变形较大，如GPS坐标反算边长与全站仪实测边长存在不同程度的差值。当边长变形值大于一定限差时，就会影响平面控制精度，给工程放样等带来众多不便。建立工程平面控制系统首先应该解决的是长度变形问题，即通过数据处理使平面控制系统的边长的理论数值与实测边长数值尽量接近，从而满足工程测量的需要。

1 投影边长变形的原因及规律

实地边长归算到高斯平面上需要经过2次投影，即高程归算投影和高斯投影。边长变形就是这2次投影变形所致。

1）实测边长归算到参考椭球面边长的变形影响,即高程归算变形ΔS1为：

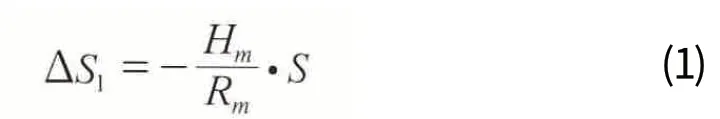
式中，Hm为归算边高出参考椭球面的平均大地高。

2）将参考椭球面上的边长归算到高斯面上的变形影响，即高斯投影变形ΔS2为：

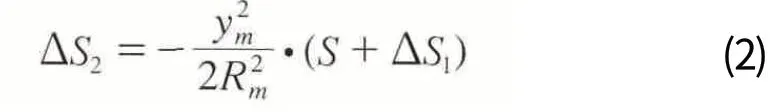
式中，S为归算边的长度，即已经换算到边长两端点的平均高程面上的水平距离；Rm为参考椭球面在测区内的平均曲率半径；ym为归算边两端点横坐标平均值,即边长S两端点在统一3°带高斯平面上横坐标的平均值。

从式（1）、式（2）可以看出投影变形的主要特征有：

1）地面实测长度归算到参考椭球面上的值总为负值，表明地面长度归算到参考椭球面上的边长变形总是缩短，实地边长与椭球面距离越大变形越大。

2）椭球面上长度归算至高斯面上变形值总为正值，表明将椭球面上长度投影到高斯面上边长总是增大，离中央子午线越远变形越大。

3）高程归化投影变形值ΔS1与高斯投影变形值ΔS2符号相反，所以在一定区域内2种变形是可以相互抵偿的，从而能有效减小长度投影的变形。

2 解决投影变形的方法

当测区直接采用国家3°带高斯正形投影平面直角坐标系，边长变形超过限差时，可根据情况采用以下坐标系统加以解决。

2.1 抵偿投影面的3°带高斯投影平面直角坐标系统

此系统是人为地改变归化高程，即改变ΔS1使之抵偿高斯投影的长度变形ΔS2，但并不改变统一3°带的中央子午线的投影改化方法。就是说，此坐标系中依然采用国家统一的3 °带投影，但投影的高程面不是参考椭球面而是根据补偿高斯投影长度变形而选择的高程参考面。令

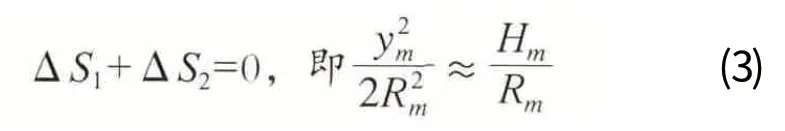
由于采用国家3 °带投影，这时ym一定。设投影面（补偿面）到归算边的高差为ΔH，则有：

则系统投影面（抵偿面）的高程为：

2.2 任意带高斯正形投影的平面直角坐标系

此坐标系中，仍把地面观测结果归算到参考椭球面上，但投影带的中央子午线不按国家3°带划分，而是选择通过测区中心的一条子午线作为中央子午线。此系统适用于测区位于中央子午线附近且海拔不太高的地方。

2.3 具有高程抵偿面的任意带高斯正形投影平面直角坐标系

这是综合了上述2种坐标系长处的一种任意高斯直角坐标系。此坐标系中，用测区平均高程面代替参考椭球面作为投影面，计算时以测区中心的子午线代替统一3°带的主子午线来计算坐标值。这样可以使测区边长的高程归化和距离改化值明显减小，从而控制投影长度变形。

3 应用实例

包删可勒水利枢纽工程所在位置地理坐标为东经83°13′～83°16′，北纬43°18′～43°22′。测区位于恰甫河河谷地带的高山地，呈东西向带状，距中央子午线70 km左右。平均海拔约1 100 m，测区高差高于130 m。从位置及高程来看测区明显存在着投影变形，其变形量如表1、表2所示。

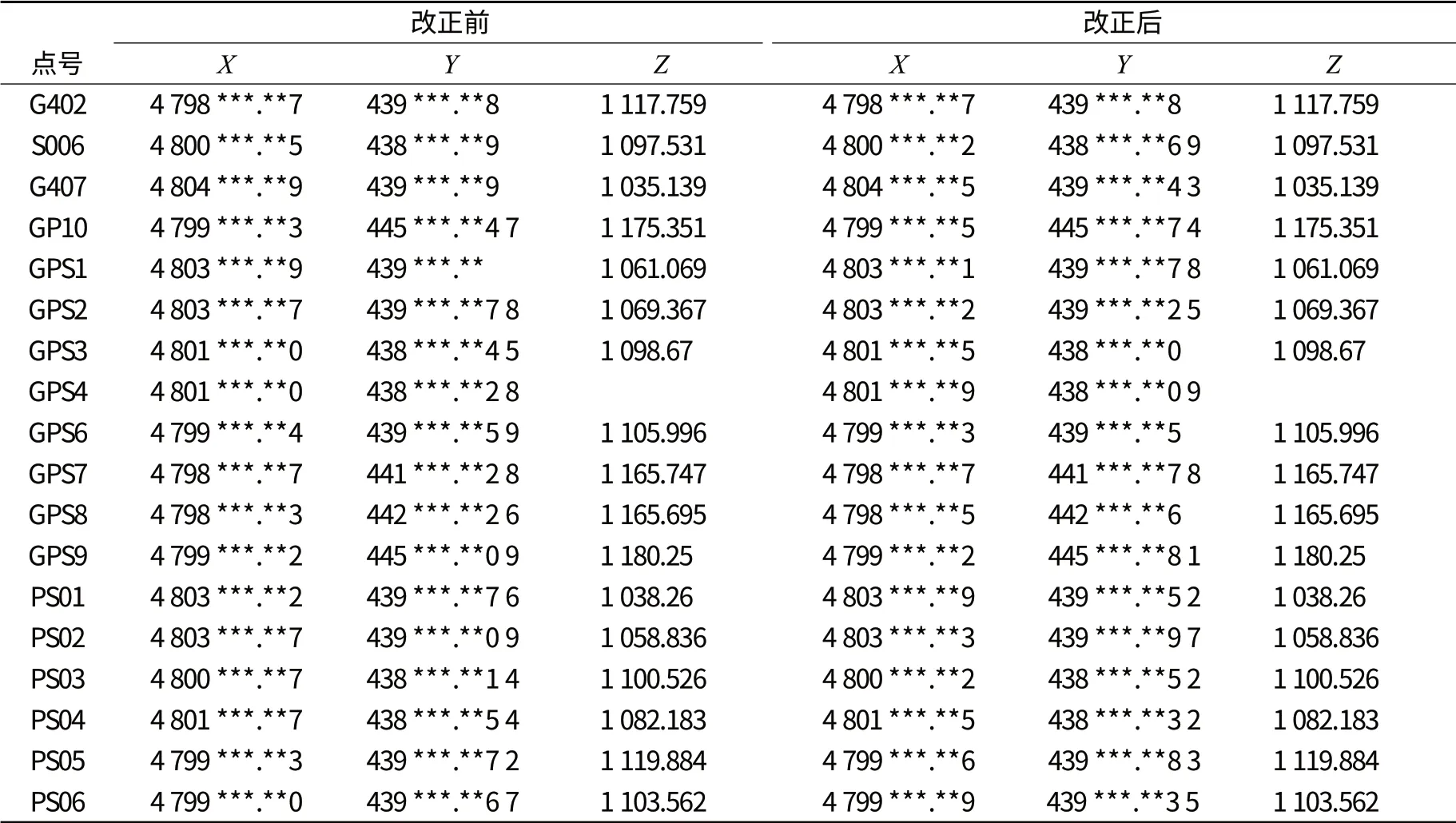
表1 改正前后对照表

表2 变形量计算表

①测区平均高程为1 100 m；②按测区纬度求得参考椭球面在测区内的平均曲率半径为6 376 km。

从表中数据可以看出，满足高斯投影变形小于2.5 cm/km的有2个系统:“统一3°带抵偿坐标系统”和“具有高程抵偿面的任意坐标系统”。因前者计算相对简单一些，我们确定选择前者，即投影带为统一3°带、投影面为820 m、抵偿投影后变形量残差为0.4 mm/ km的统一3°带抵偿坐标系统。最后将成果与全站仪边长进行了实测比对，结果非常吻合，达到了解决投影变形提高控制网精度及方便使用的预期目的。

4 结 语

实践证明，要满足《工程测量规范》规定的平面控制网坐标系统投影长度变形不大于2.5 cm/km（1/40 000）的要求，直接采用国家标准3°带投影，必须具备2个条件：①测区位置位于高斯正形统一3°带中央子午线附近（40 km左右）；②测区平均高程面必须接近参考椭球面或平均海水面（100 m以下）。）同时能够满足上述条件的测区并不多，因此在建立平面坐标系统时，应根据测区的地理位置及平均高程来确定所采用的坐标系统。通过选择合适的投影面或中央经线，能有效地解决控制系统边长变形的问题，有效弥补高斯投影国家统一3°带的局限性，从而提高控制网精度及方便直接使用常规测量仪器放样。

[1]邹时萌. 城市测量手册[M]. 北京：测绘出版社, 1993

[2]李青岳.工程测量学[M]. 北京：测绘出版社,1984

[3]金玉山.具有抵偿高程面的任意带坐标系设计原理与方法[J].铁道勘察 ，2005(4)：26-27

[4]DL/T 5173-2003.水电水利工程施工测量规范[S].

[5]GB50026-2007.工程测量规范 [S].

[6]孔祥元 .大地测量学基础[M].武汉 ：武汉大学出版社,2010

[7]杨大勇， 王坚. 公路控制测量中坐标系的选择[J].科技信息，2011(18):30