电动车动力总成内部激励的研究分析＊

方 源， 章 桐，3， 于 蓬， 郭 荣

（1.同济大学新能源汽车工程中心 上海，201804）

（2.同济大学汽车学院 上海，201804） （3.同济大学中德学院 上海，201804）

1 问题的引出

电动汽车的核心部件——电驱动系统正朝着集成高效的方向发展，电机－变速器一体化驱动系统就是典型的集成式驱动模式之一［1］。一体化的驱动系统为振动噪声（noise vibration and harshness，简称NVH）的研究提出了新的难题，例如集成驱动系统由于耦合电机与减速器，所以固有特性发生改变，此外，影响其NVH特性的内激励也有所不同。一些文献将一体化系统简化为两质量结构，并进行了振动特性的研究［2-7］。这些文献都是将系统视为具有固定振动特性的两质量系统，并不能真实地反映集成驱动系统的固有特性［8］。针对内激励引起振动噪声的问题，国内外学者已有较多研究，但是仍存在不足：在考虑电磁激励时忽略了切向电磁力波的作用［2-5］，而针对电机－减速器集成驱动系统，有必要考虑电磁切向力波；在进行电磁仿真分析时，通常施加理想的三相正弦电流，没有考虑外电路电阻、电感等元件的影响［2-5］；在考虑齿轮系内激励时，忽略了齿轮啮合冲击力的作用［6-7］。

笔者对电动动力总成（见图1）内部动态激励进行了分析研究，综合考虑了电磁径切向力、转矩波动、外电路、齿轮时变啮合刚度、误差以及齿轮啮合冲击激励。

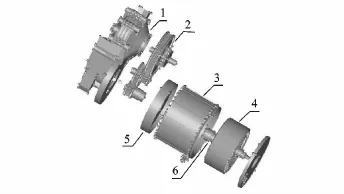
图1 电机－减速器实体几何模型Fig.1 Geometry model of motor－reducer

2 电磁激励

由于电机的缘故，电动汽车动力总成内部激励与传统汽车相比有了本质区别，电磁激励成为影响其振动噪声特性的关键因素。

针对电机的电磁激励，国内外研究工作绝大多数仅考虑理想电流激励下，电磁径向力对电机振动噪声特性的影响，这对于电动车车用动力总成来说是远远不够的。

笔者将充分考虑电磁径向力、电磁转矩以及外电路对电动动力总成激励的影响。

2.1 电磁力波

动力总成结构在电磁场中受到的电磁力［9］可表示为

麦克斯韦尔电磁力是产生电机振动噪声的主要原因。在极坐标中，用麦克斯韦应力张量法描述作用在铁磁物质一侧表面上的应力为

其中：Fr，Ft分别为作用在铁磁物质表面上的径向、切向麦克斯韦尔电磁力；μ为铁磁物质交界面上一侧介质的磁导率；Br，Bt分别为一侧介质中的径向、切向磁通量密度。

2.2 场路耦合

将电机电磁场模型与控制系统电路模型进行耦合分析，可以综合考虑外部电路与电机磁场的相互作用。

2.2.1 场路耦合离散模型

永磁同步电机场路耦合离散模型如图2所示。

图2 电机电枢绕组等效电路Fig.2 Motor armature winding circuit

设控制电路u相桥臂的输出电压为uu，则u相绕组的电压平衡方程式可以表示为

其中：eu为u相绕组的感应电势；Ru为定子相电阻；iu为相电流；Lu为定子u相漏感值。

电动势可以表示为绕组交链的磁链对时间的导数，而磁链与绕组区域的矢量磁位有关。相绕组的感应电势［10］可以表示为

其中：P为电机极对数；Lef为电枢长度；χ为单元的绕组电流系数；Ae为三角形单元面积；n为单元总数；N为线圈匝数；S为单个绕组的面积；a为定子绕组并联路数。

由式（4）和式（5）可得到离散化方程

根据文献［11］，用加权余量法建立有限元离散化方程，取权函数等于形状函数，并电磁场方程作离散化处理，得瞬态电磁场的离散化方程为

根据式（6）的绕组电路方程耦合离散模型与式（7）的瞬变电磁场计算模型，求得场路耦合离散方程式为

2.2.2 基于场路耦合的电机仿真分析

由于旋转电动机的磁场分布沿轴向变化足够小，一般的旋转电动机电磁场问题可简化成一个二维电磁场问题来分析。首先使用有限元软件Ansoft／Maxwell，建立电磁场分析模型，如图3所示。

为了考虑外电路对电机特性的影响，笔者利用Simplorer软件搭建外部模型，包括逆变器驱动电路、SPWM控制部分和 Maxwell Co－simulation的电机模块，如图4所示。通过将外部控制电路得到的电机三相电流，传递到电磁分析模型中作为激励信号，经过有限元电磁场分析得到此时电机的转矩和转速，再实时传递到控制系统中作为下一个计算时间步长的输入反馈信号，进而分析出在整个仿真周期内电机及其控制系统的性能。仿真工况如下：电机转速为3kr／min；负载为12Nm。

图3 电机二维电磁场模型（单位：mm）Fig.3 Electromagnetic field model（unit：mm）

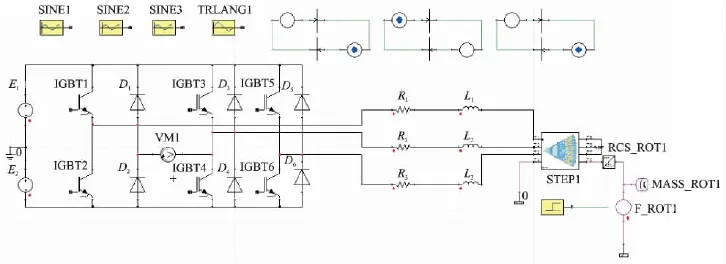
图4 电机外电路Fig.4 External circuit

图5（a）为电机的三相电流时域图，从图中可以看出，电流曲线有一些毛刺现象，而不是理想的三相正弦电流，这是因为受到电路中的电感等电子元件的影响。通过频域分析，从图5（b）中可以看出，在低频处的100，400以及800Hz处产生了一些谐波，这些电流谐波最终会对动力总成的振动噪声产生影响。图6为电机的电磁转矩曲线，从图中也可看出，最终的转矩稳定在12Nm附近，并有较大波动。通过频域分析得知，在2kHz处存有较多谐波分量，而在开关频率及其2倍频附近也存在部分谐波分量，由此可以看出开、关频率对电机转矩波动有较大影响。笔者设置开关频率为10kHz，在后续的工作中需要对开关频率进行研究，折衷考虑电机的功耗、成本以及电磁振动噪声，选择合适的开关频率。由于动力总成是将电机与减速器集成在一起的，所以电磁波动转矩对动力总成的振动噪声也会产生影响，必须加以考虑。图7为电机径向电磁力波，呈周期性变化，其峰值达到了8×105N／m2，从其频域图中可以看出，在2kHz以内存在多个峰值频率。研究发现，电机径向力是产生电磁振动噪声最主要的原因，因此，一方面要注重减小径向力的幅值，另一方面要避免一些电磁力的谐波分量出现在动力总成的固有频率处。图8为电机产生的切向电磁力时频域图。尽管其幅值与径向力相比存在数量级的差距，但是在2kHz内有较多峰值，而且动力总成是由电机与减速器集成在一起的，并不是对称的圆柱结构，所以切向电磁力对动力总成的振动噪声也会产生影响，必须加以考虑。

图5 电机三相电流Fig.5 Three phase current

3 齿轮传动系内部激励

齿轮系统的内部激励是由于同时啮合齿对数的变化、轮齿受载变形、齿轮制造误差等因素所引起的，它包括刚度激励、误差激励和啮合冲击激励。

图6 电磁转矩Fig.6 Electromagnetic torque

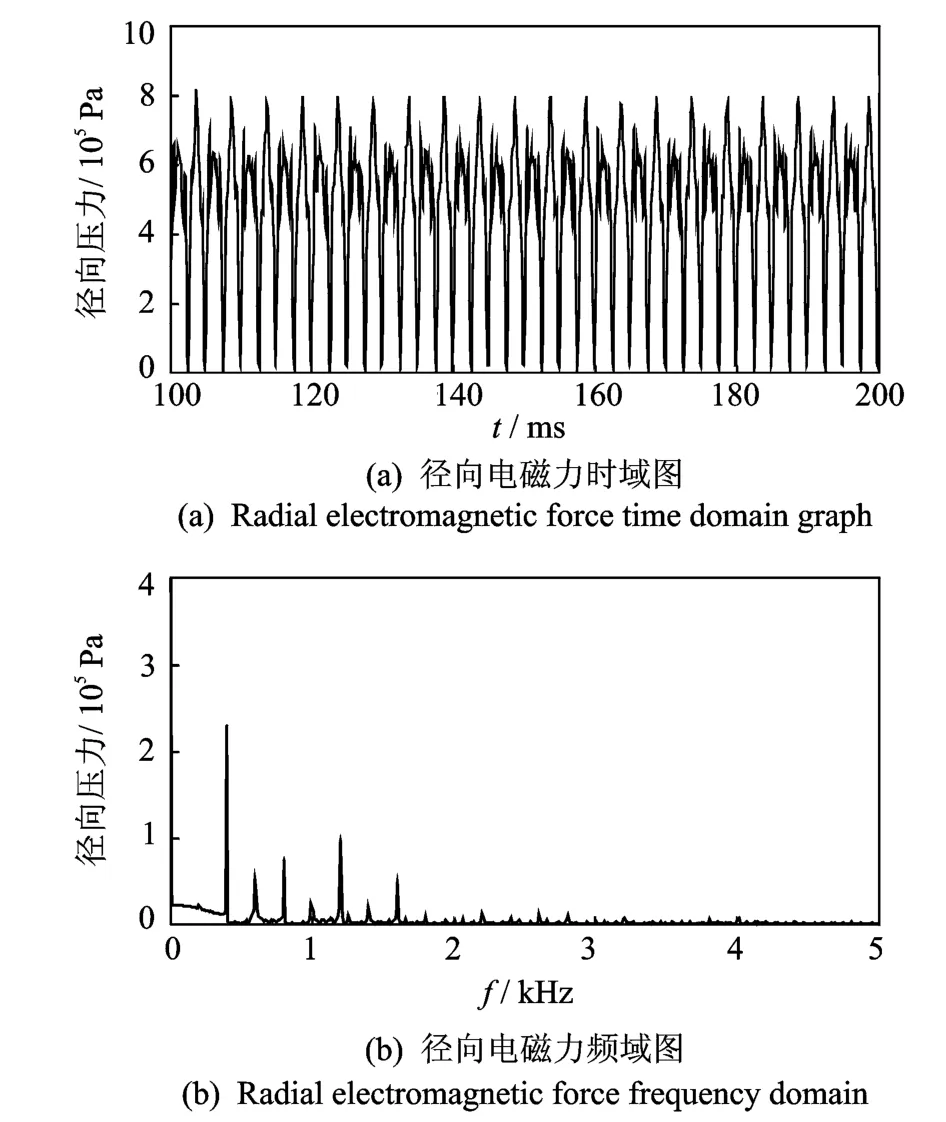
图7 径向电磁力Fig.7 Radial electromagnetic force

图8 切向电磁力Fig.8 Tangential electromagnetic force

图9 电动汽车传动系统结构简图Fig.9 Driving system structure diagram

图10 齿轮传动系几何模型Fig.10 Geometric model of gear transmission system

笔者研究的动力总成齿轮传动系由两级齿轮传动组成，均采用斜齿轮传动，其结构简图与几何模型如图9、图10所示。输入轴9通过轴的内花键与电动机输出轴相连接，动力由电动机输出，经小齿轮1传到中间轴大齿轮2上，大齿轮2带动中间轴和小齿轮3一起转动，小齿轮3将动力传递给齿圈4，齿圈4带动差速器壳体11转动。由于两个行星齿轮5，6通过行星齿轮轴与差速器壳体连接在一起，行星齿轮与差速器壳体同步转动，并通过齿轮啮合将动力分别传给左右半轴齿轮7和8，再通过半轴传递动力到车轮。齿轮传动系的参数如表1所示。

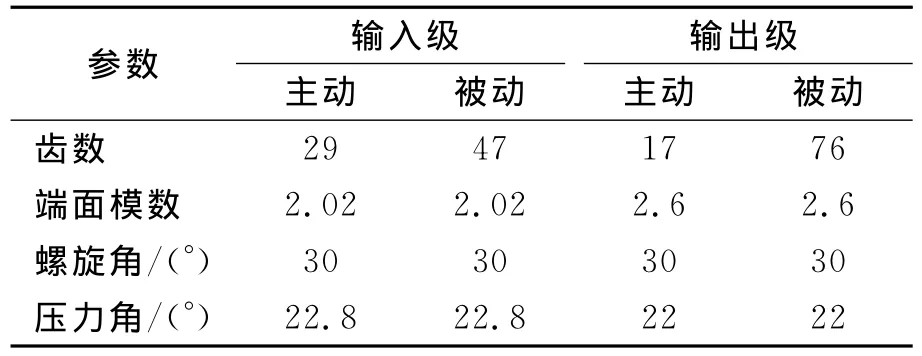
表1 齿轮参数Tab.1 Gear parameter

3.1 齿轮啮合时变刚度

齿轮啮合过程中，参与啮合的轮齿对数会随时间做周期变化，同时轮齿在从齿顶到齿根的啮合过程中，弹性变形也不断变化，这些因素都导致了齿轮啮合刚度的变化。

笔者研究的斜齿轮传动，啮合线是“点－线－点”的变化过程，啮合过程的轮齿交替并不是突变的。由于啮合过程中轮齿的综合啮合刚度以及轮齿载荷也是周期性变化的，同样会引起啮合过程的动态刚度激励。对于宽齿斜齿轮副，当单位接触线长度的啮合刚度为常数k0时，其时变啮合刚度可以用时变齿轮副接触长度L（τ）［12］来表示

其中：τ＝t／Tz，Tz为啮合周期；k0＝ （0.25εα＋0.75）c′。

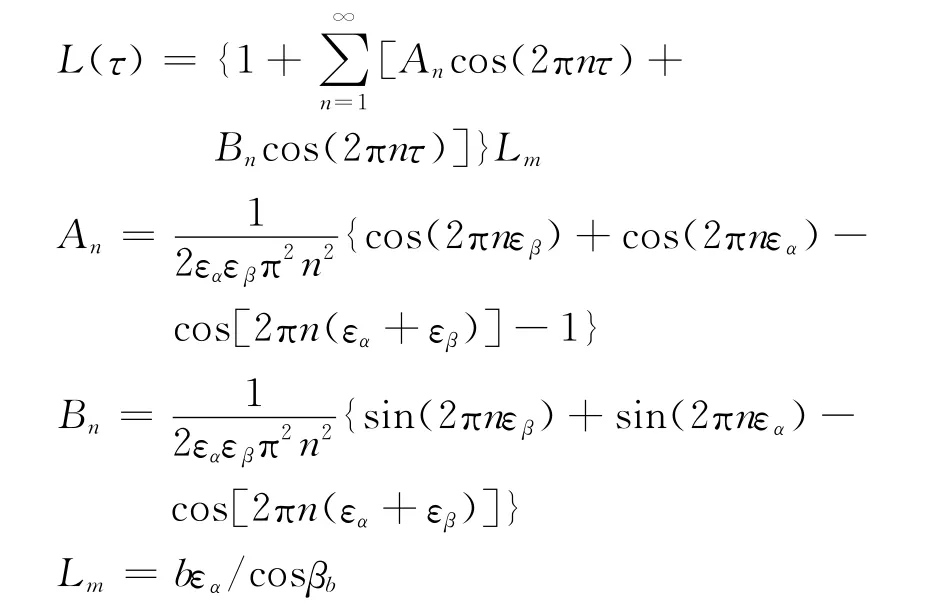
其中：εα为端面重合度；εβ为轴向重合度；βb为基圆螺旋角；b为齿宽；c′为直齿圆柱齿轮刚度。

以输入级转速3kr／min为条件，根据表1所示的齿轮参数，通过Matlab编程，求解并绘制出输入级、输出级齿轮时变啮合刚度的数值模拟曲线，如图11所示。

图11 时变啮合刚度曲线Fig.11 Time－varying meshing stiffness

3.2 齿轮误差激励

由于齿轮加工误差和安装误差，使得齿轮啮合齿廓偏离理论的理想位置而引起齿轮瞬时传动比发生变化，使齿轮啮合时发生碰撞与冲击，从而产生齿轮啮合的误差激励。由文献［6］中的方法可知，七级精度的减速器齿轮误差曲线如图12所示。

图12 误差曲线Fig.12 Meshing error

3.3 啮合冲击力

齿轮箱在啮合过程中，由于轮齿变形和轮齿误差的存在，使轮齿在啮入和啮出时的啮合点相对理论啮合线产生偏移，从而引发啮入、啮出冲击载荷，这种冲击激励称为啮合冲击激励。考虑到啮入冲击的影响比啮出冲击大，因此这里只考虑啮入冲击的影响［13－15］。

其中：ω为主动轮的角速度；i为齿轮副传动比；αb为齿轮分度圆上的压力角；α′E1＋γ′1为幅角；qE1为幅角啮合齿轮副的柔度；J1，J2为齿轮惯性矩；b为齿宽；rg1，rg2为齿轮的当量基圆半径。

通过计算并绘制出输入级、输出级齿轮冲击激励曲线，如图13所示。

图13 齿轮冲击激励Fig.13 Meshing impact

由图13可以看出，冲击载荷的频率即为齿轮啮合频率。输入级齿轮啮合冲击载荷峰值接近4.5 kN，远大于齿轮时变刚度产生的1.5kN的动载荷；输出级的冲击激励幅值接近3.5kN，也远大于齿轮时变刚度产生的500N的动载荷。尽管齿轮冲击载荷的作用时间相对较短，但由于其幅值很大，仍会对齿轮传动系振动噪声产生影响，因此，考虑齿轮传动系统内部激励时不能将其忽略。

3.4 综合激励

将时变啮合刚度曲线和误差曲线在对应点处相乘，并在对应的时刻加上冲击激励，得到图14所示的包括刚度激励、误差激励及啮合冲击激励的齿轮内部综合激励曲线。

由图14可知，系统的综合动态激励呈现出间歇性的规律，由于啮合刚度激励、误差激励、冲击激励的综合影响，随着啮合刚度、误差和冲击力的时变性，系统综合动态激励也具有时变性。

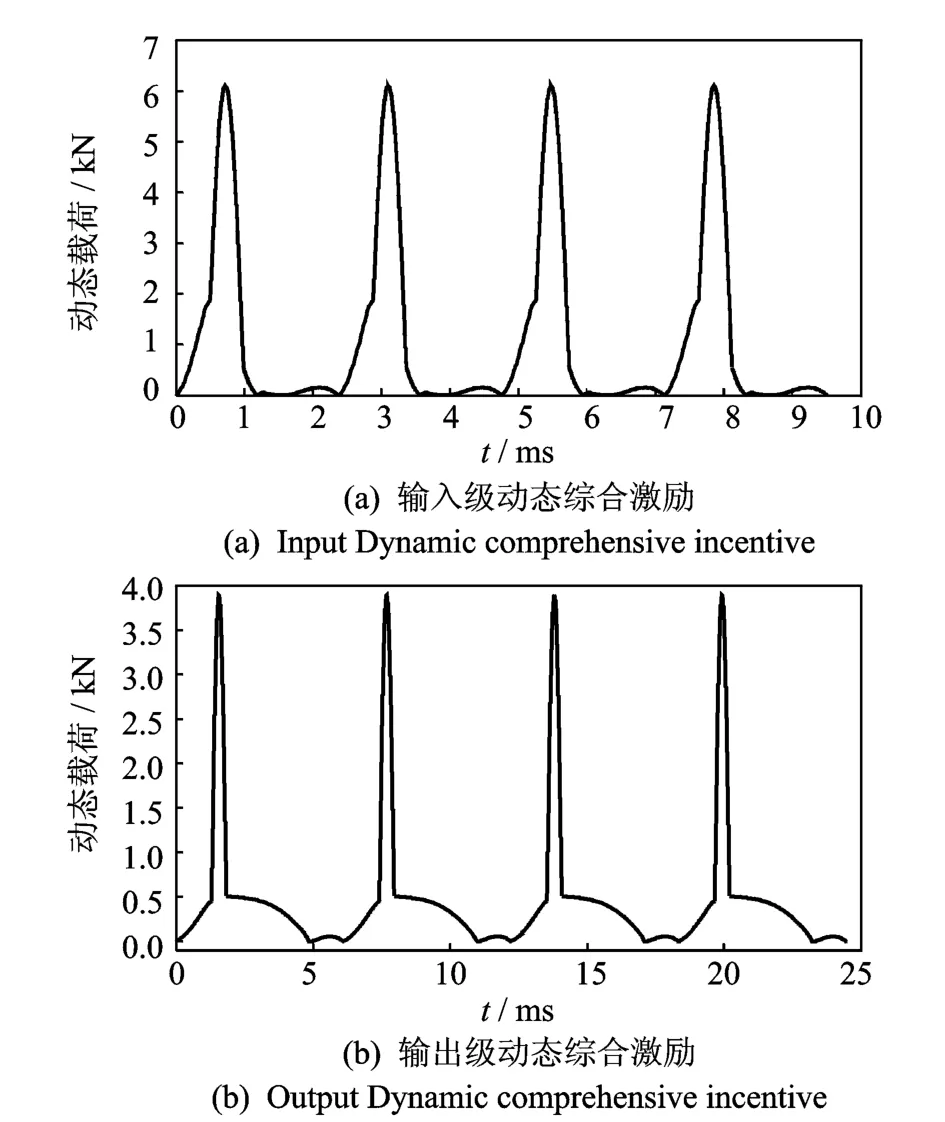
图14 齿轮啮合综合动态激励Fig.14 Gear mesh comprehensive dynamic incentive

4 结 论

1）搭建电机外电路，提出了基于场路耦合的永磁同步电机电磁仿真分析的基本方法，综合考虑了外部电路对电磁激励的影响，并求得电机径、切向电磁力波以及电磁转矩。

2）对齿轮传动系统中齿轮时变啮合刚度、误差激励以及冲击激励进行数值模拟，得到了动力总成齿轮动态啮合激励。

3）尽管在电驱动动力总成振动特性的研究领域取得一些进展，但是，本研究忽略了外部激励的影响，如齿轮旋转质量不平衡、几何偏心、负载的转速与扭矩波动以及系统中有关零部件的激励特性，如滚动轴承的时变刚度。今后的研究工作有必要对各种激励加以详细地考虑。

［1］ Ishikawa Y.A motor－drive system design that take into account EV characteristics［C］∥SAE Technical Paper.doi：10.4271／1999－01－0739：1－9.

［2］ Pellerey P，Lanfranchi V，Friedrich G.Coupled numerical simulation between electromagnetic and structural models，influence of the supply harmonics for synchronous machine vibrations［J］.Magnetics，IEEE Transactions on，2012，48（2）：983－986.

［3］ Schmulling B，Kasper K，Hameyer K.Acoustic optimization of a switched reluctance machine using numerical simulation［C］∥ICEM.Greece：［s.n.］，2006.

［4］ Schlensok C，van Riesen D，Küest T.Acoustic simulation of an induction machine with squirrel－cage rotor［J］.The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2006，25（2）：475－486.

［5］ 王玎，祝长生，符嘉靖.基于有限元的异步电机电磁振动分析［J］.振动与冲击，2012，31（2）：140－144.

Wang Ding，Zhu Changsheng，Fu Jiajing.Electromagnetically excited vibration analysis for an asynchronous electrical machine with finite element method［J］.Journal of Vibration and Shock，2012，31（2）：140－144.（in Chinese）

［6］ 刘辉，张喜清，项昌乐.多源动态激励下变速器箱体［J］.兵工学报，2011，32（2）：129－135.

Liu Hui，Zhang Xiqing，Xiang Changle.Dynamic response analysis of gearbox housing under multi－source dynamic excitation［J］.Acta Armamentarii，2011，32（2）：129－135.（in Chinese）

［7］ 周建星，刘更，马尚君.内激励作用下齿轮箱动态响应与振动噪声分析［J］.振动与冲击，2011，30（6）：234－238.

Zhou Jianxing，Liu Geng，Ma Shangjun.Vibration and noise analysis of gear transmission system［J］.Journal of Vibration and Shock，2011，30（6）：234－238.（in Chinese）

［8］ 方源，于蓬，章桐.电动车动力总成模态试验与仿真分析［J］.机械传动，2012（4）：110－113.

Fang Yuan，Yu Peng，Zhang Tong.Test and simulation analysis of modal parameter of an electric automotive powertrain［J］.Journal of Mechanical Transmission，2012（4）：110－113.（in Chinese）

［9］ 汤蕴璆.电机内的电磁场［M］.2版.北京：科学出版社，1998：341－363.

［10］刘瑞芳，严登俊，胡敏强.永磁无刷直流电动机场路耦合运动时步有限元分析［J］.中国电机工程学报，2007，27（12）：59－63.

Liu Ruifang，Yan Dengjun，Hu Minqiang.Field circuit and movement coupled time stepping finite element analysis on permanent magnet brushless DC motors［J］.Proceedings of the CSEE，2007，27（12）：59－63.（in Chinese）

［11］唐政，黄大贵.基于场路耦合时步有限元的永磁同步电动机瞬态特性研究［J］.微电机，2008，41（11）：11－14.

Tang Zheng，Huang Dagui.Study on transient characteristic of permanent magnet synchronous motor based on field－circuit coupled time－stepping finite element method［J］.Micromotors，2008，41（11）：11－14.（in Chinese）

［12］李瑰贤，马亮，陶建国，等.舰船用齿轮传动啮合刚度及动态性能研究［J］.船舶工程，2000（5）：41－43.

Li Guixian，Ma Liang，Tao Jianguo，et al.A study on meshing rigidness and dynamic property of gear transmission used for the warship［J］.Ship Engineering，2000（5）：41－43.（in Chinese）

［13］武保林，杨素君，姚俊红.齿轮传动中啮合冲击的理论分析［J］.机械科学与技术，2003，22（1）：55－57.

Wu Baolin，Yang Sujun，Yao Junhong.Theoretical analysis on meshing impact of involute gears［J］.Mechanical Science and Technology，2003，22（1）：55－57.（in Chinese）

［14］王玉芳，童忠钫.齿轮加速度噪声的研究［J］.振动与冲击，1991（1）：42－46.

Wang Yufang，Tong Zhongfang.Research on the gear acceleration noise［J］.Journal of Vibration and Shock，1991（1）：42－46.（in Chinese）

［15］张德满，李舜酩，尚伟燕.工程机械机外噪声声源分析及降噪处理［J］.振动、测试与诊断，2011，31（3）：362－365.

Zhang Deman，Li Shunming，Shang Weiyan.Outside noise analysis and control for construction machinery［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31（3）：362－365.（in Chinese）