二阶线性系统调参共振的特征信号检测＊

冷永刚， 刘 瑜， 赖志慧， 范胜波

（1.天津大学机械工程学院 天津，300072）

（2.天津大学机构理论与装备设计教育部重点实验室 天津，300072）

引 言

在信号检测中，某些包含特征信息的微弱信号常常被强干扰噪声所淹没。如何从干扰噪声背景中检测出微弱的特征信息，一直受到人们的广泛关注。已有的一些检测方法，如FFT谱分析、小波变换等是一种基于函数的信号处理方法，这些方法在有限采样数据长度的强干扰噪声条件下不能很好地检测出微弱特征信息［1-4］，其应用受到限制。随机共振和混沌的检测方法是一种基于非线性动力系统的非线性信号处理方法，这种非线性检测方法可对较低信噪比的微弱特征信息有较好的检测效果［5-7］。随机共振方法通常需要建立过阻尼的合适的双稳系统［8］，而混沌方法需要预先给定与待检测信号同频的驱动项［9-10］。笔者提出一种基于二阶线性动力系统参数调节共振的信号处理方法，该方法利用二阶线性系统响应的共振特性来检测噪声中的微弱特征信息，其检测原理简单，为信号检测与处理提供了一种可行的方法。

1 检测原理

1.1 检测模型

以常规的单自由度二阶线性系统为研究对象，其系统模型为

其中：ζ为系统的阻尼比；ωn为系统的无阻尼固有频率，以下简称固有频率；s（t）为系统的激励力。

如果式（1）的激励是一正弦激励信号，那么其稳态响应是与该正弦信号频率相同的受迫振动响应。当激励频率等于系统的固有频率时，系统响应达到最大，即发生共振［11］。

根据线性系统响应的共振特性，笔者提出一种基于二阶线性系统调参共振的微弱信号检测方法，其基本原理是：把包含有特征频率成分和噪声干扰的待检测信号当作系统的激励s（t），而把自由振动方程（1）看作信号处理模型，那么通过人为调节系统的固有频率参数，使其与待检测信号中的特征频率相等，于是系统响应达到共振，进而使特征信号进一步突出而克服噪声，达到检测特征信号成分的目的。

设待检测信号s（t）由单频正弦信号Asin（ω0t）和高斯白噪声n（t）组成，则式（1）变为

其中：A和ω0分别为正弦信号的幅值和频率；噪声，D为噪声强度；ξ（t）是均值为0、方差为1的高斯白噪声。

1.2 线性系统的响应特性

当激励力仅是正弦信号，式（2）的解为

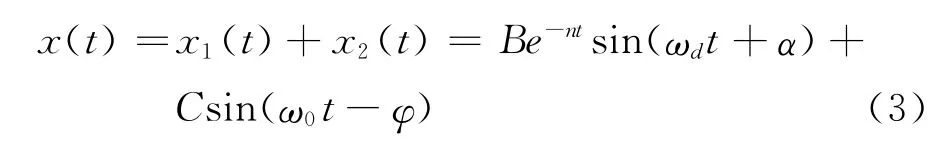
其中：n＝ζωn；；α，φ 为相位差。

由式（3）可知，受迫振动由两部分构成：前一部分是圆频率为ωd的衰减振动；后一部分是圆频率为ω0的受迫振动。在实际情况中，由于阻尼的存在，衰减振动所产生的暂态过程经过一定的时间之后就消失了，所以主要研究后一部分的稳态过程［11］。稳态受迫振动的振幅可表示为

由式（4）做C－ω0／ωn关系图，如图1所示。图1的特性是：在过阻尼条件下，振动的衰减快，振幅单调递减；在欠阻尼比时，如果系统固有频率与信号频率逐渐接近，那么振动的振幅将逐渐增大；当固有频率与信号频率相等时系统响应达到共振，此时阻尼比对共振峰影响很大，阻尼比减小会引起共振峰值的增大。

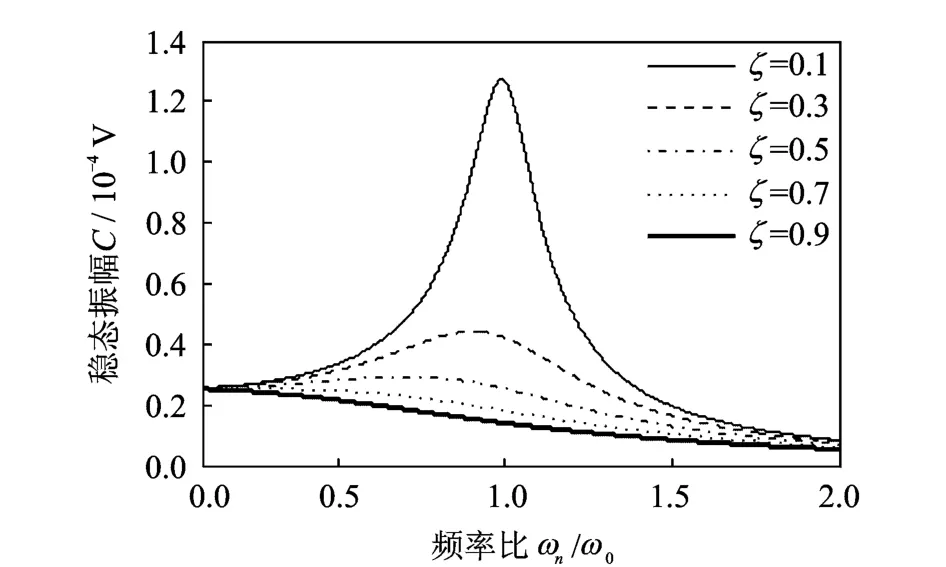
图1 正弦信号激励下的稳态振幅曲线Fig.1 The steady－state amplitude curve under simulation of sinusoidal signal

若输入激励力信号只是强度为D的高斯白噪声，则模型（2）变为

根据线性系统叠加原理，白噪声经过线性系统的幅频特性可看成是无穷多个不同频率的正弦信号幅频特性的叠加。因此不难知道，输出信号频谱特征仍然是图1的形式，只不过图1横轴变量不再是频率比ω0／ωn，而是频率ω，表示所有噪声响应频率成分，系统的共振特性始终存在。图1纵轴响应幅值变量C根据式（4）相应变为

当二阶线性系统同时受到正弦信号Asin（ω0t）和白噪声的激励时，根据线性系统的叠加原理，可得到系统稳态输出响应幅值为

式（7）在欠阻尼条件下，当调节系统固有频率与信号特征频率相等时系统响应达到共振。在信号频率处，信号引起的系统共振与噪声引起的系统共振叠加，响应幅值可以在信号特征频率处进一步得到加强，从而可以突出噪声中的特征信号而达到检测目的。

1.3 特征信号检测方法

根据二阶线性系统共振特性，在频域内以变化的系统固有频率ωn为横坐标，以每个ωn所对应系统输出信号的最大幅值Cmax为纵坐标作图，可得Cmax－ωn曲线，如图2所示。其中：系统阻尼比ζ＝0.2，正弦信号幅值和频率为A＝0.1和ω0＝10，噪声强度D＝2，采用四阶Runge－Kutta法求解式（2），数值步长Δt＝0.005，数据点数N＝10 000。Cmaxωn曲线中系统固有频率的变化步长为Δωn＝0.1。

由图2（a）可以看出，随着固有频率的变化，系统只在正弦信号激励下的响应呈现图1典型的共振曲线特性。由图2（b）可以看出，随着系统固有频率的增大，系统只在噪声作用下的响应的最大幅值变化是单调递减的。当正弦信号与噪声同时作用于系统时，由线性系统叠加性，其响应为两者响应的叠加，响应的最大幅值变化如图2（c）所示。由图2（c）知，在固有频率ωn＝ω0＝10处出现一个极大值，依此可以判断噪声中微弱信号的存在。

2 仿真分析

对于式（2），取阻尼比ζ＝0.2，正弦信号幅值和频率分别为A＝0.1和f0＝10Hz，噪声强度D＝2，数值步长Δt＝0.005s，数据点数N＝10 000，则系统输入信噪比为－29.06dB，此处输入信号的信噪比定义为：在数值分析长度固定条件下，待测正弦信号的总功率与噪声信号的总功率之比。系统输入信号的频谱如图3所示，在f0＝10Hz处看不到正弦信号特征的存在。当固有频率fn取包含信号频率f0＝10Hz在内的范围值变化时，如fn＝5，8，10，15 Hz时，系统输出信号的频谱变化情况如图4所示。

由图4可以看出，当系统固有频率由小增大时，系统响应频域的最大幅值会逐渐减小，不宜判断噪声中的微弱特征正弦信号。但是通过系统输出信号的最大幅值Cmax与固有频率fn关系曲线，如图5Cmax－fn曲线，可以在fn＝10Hz处得到一个极大值，从而可以检测到微弱的特征正弦信号频率。

图2 二阶线性系统的正弦、噪声及其叠加响应Fig.2 Response of the second order linear system with the input of sinusoidal，noise and both of them

图3 输入信号频谱图Fig.3 Spectrum of input signal

图4 不同固有频率下输出信号的频谱图Fig.4 Spectrum of output signals with different inherent frequencies

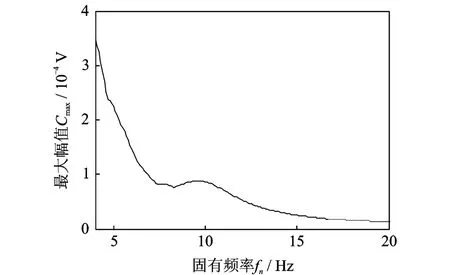
图5 系统响应Cmax－fn关系曲线Fig.5 The system response curve between Cmaxand fn

3 系统阻尼比参数的调节

在式（1）线性系统响应的共振点处，阻尼比参数ζ的影响很大，进而对特征信号的检测结果也会产生很大影响。根据ζ的取值不同，线性系统可分为过阻尼系统（ζ＞1）、临界阻尼系统（ζ＝1）和欠阻尼系统（ζ＜1）。对于过阻尼系统和临界阻尼系统，由于其幅频特性曲线是单调递减的，所以笔者提出的检测方法不适用于过阻尼和临界阻尼情况，只适用于能够产生共振的、非单调频响的欠阻尼情况。

针对欠阻尼情况，从系统响应幅值式（4）可知，在共振点处，阻尼比ζ越小响应幅值越大。例如，仍取图4参数：A＝0.1，f0＝10Hz，D＝2，计算步长Δt＝0.005s，数据点数N＝10 000，取固有频率fn的变化步长Δfn＝0.1Hz（为了准确检测特征信号频率，系统固有频率fn的变化步长应小于频率分辨率1／N＊Δt）。当阻尼比ζ 分别为0.4，0.3，0.2，0.1，0.01，0.001时，得到如图6的Cmax－fn曲线结果。在欠阻尼情况下，ζ＞0.4时曲线单调递减变化，不宜用于检测微弱特征信号。当0.4＞ζ＞0.1时，可以在Cmax－fn曲线上找到极大值点，从而能够检测到微弱特征信号。当0.1＞ζ后，Cmax－fn曲线上会出现不止一个极大值，检测效果容易受到干扰。因此，当阻尼比过小时，噪声的波动影响会同时增大，也不宜用于检测微弱的特征信号。总之，由于在仿真分析中，所给的信号和采样条件都是很理想的，所以阻尼比取在0.1～0.4之间检测效果最好；而实际故障的信号比较复杂，且在采样点数过少、分辨力低的情况下，特征频率处的极值极易丢失，则需要考虑采用阻尼比小于0.1的系统进行检测，使特征频率处的振幅更突出。

4 应 用

某军工转子设备以375r／min（或6.25Hz）的转速运转，该转子端部是一个六角轴端且罩有一圆形套筒密封。正常情况下，转子六角轴端与套筒内壁有一定间隙。如果转子存在诸如不平衡或不对中等故障，那么转子六角轴端有可能与套筒内壁接触碰撞。为监测转子设备的运行情况，在套筒端面安装有加速度传感器，加速度计的监测信号由数据采集设备进行实时记录。某次监测结果如图7所示，其中，采样频率为10kHz，采样点数为2 000点。

由图7频谱图可以看出，在37.5Hz及其倍频75Hz处存在明显的特征频率成分，37.5Hz频率成分不是转子的工频，而是转子工频的6倍频。这个37.5Hz频率成分是由其他干扰引起，还是由于转子本身存在故障引起需要做进一步分析。

利用笔者提出的二阶线性系统调参共振检测方法，在采样频率为10kHz、采样点数为2 000点的条件下，由于采样点数少，频率分辨力低，特征频率处的极值易丢失，故而需采用较小的阻尼比来进行检测。由图1可知，小阻尼条件下特征频率处的振幅更突出，以排除噪声的干扰。取系统参数阻尼比ζ＝0.001，系统固有频率变化步长Δfn＝0.1Hz，得到Cmax－fn极大值检测曲线结果如图8所示。可以看出，频谱特征是由转频6.25Hz及其2倍频、3倍频等高倍频谐波成分组成。该组谐波成分表明，转子可能存在不平衡或不对中等故障，这种故障可能导致转子轴端与套筒内壁发生碰摩，使得转子每旋转一周转子轴端的6个角与套筒内壁发生6次碰撞，于是在频谱图上产生37.5Hz的大振幅。由于转子本身的不平衡或不对中故障特征较弱，因此从图7的频谱中不容易识别。随后的拆机检查证实了这一诊断结论。由此可见，线性系统调参共振的方法可以处理工程中的故障信号，有效提取噪声干扰中的微弱特征信号。

图6 不同阻尼比的系统响应Cmax－fn关系曲线Fig.6 The system response curves between Cmaxand fnwith different damping ratio

图7 转子轴端振动的时域波形和频谱图Fig.7 Waveform and spectrum of the vibration signal upon the rotor spindle

图8 线性系统检测结果图Fig.8 Detection result of the linear system

5 结束语

笔者针对微弱正弦信号的检测提出了一种基于二阶线性系统调参共振的检测方法，该方法利用粘滞阻尼二阶线性系统的共振特性，通过改变系统的无阻尼固有频率，得到系统响应最大值随固有频率变化曲线，此曲线中的极大值点就是微弱正弦信号的特征频率。仿真和转子故障诊断实验表明，笔者提出的方法原理简单，能为实际信号检测与处理提供一种可行的方法。

［1］ 陈峰，成新民.基于小波变换的信号去噪技术及实现［J］.现代电子技术，2005，28（3）：11－13.

Chen Feng，Chen Xinmin.Signal denosing technique and realization based on wavelet transform ［J］.Modern Electronics Technique，2005，28 （3）：11－13.（in Chinese）

［2］ Newland D E.Ridge and phase identification in the frequency analysis of transient signals by harmonic wavelets［J］.Journal of Vibration and Acoustics－Transactions of the ASME，1999，121（2）：149－155.

［3］ 陶新民，徐晶，刘兴丽，等.基于最大小波奇异谱的轴承故障诊断方法［J］.振动、测试与诊断，2010，2（1）：78－82.

Tao Xinmin，Xu Jing，Liu Xingli，et al.Fault diagnosis of bearing using maximum wavelet singular spectrum［J］.Journal of Vibration，Measurement ＆Diagnosis，2010，2（1）：78－82.（in Chinese）

［4］ 陈果.一种改进的谐波小波及其在转子故障诊断中的应用［J］.机械工程学报，2011，47（1）：8－16.

Chen Guo.An improved harmonic wavelet and its application to rotor fault diagnosis［J］.Journal of Mechanical Engineering，2011，47（1）：8－16.（in Chinese）

［5］ Jung P，Hanggi P.Amplification of small signal via stochastic resonance［J］.Physical Review A，1991，44（12）：8032－8042.

［6］ 冷永刚，王太勇，郭焱，等.双稳随机共振参数特性的研究［J］.物理学报，2007，56（1）：30－35.

Leng Yonggang，Wang Taiyong，Guo Yan ，et al.Study of the property of the parameters of bistable stochastic resonance［J］.Acta Physica Sinica，2007，56（1）：30－35.（in Chinese）

［7］ 聂春燕.混沌系统与弱信号检测［M］.北京：清华大学出版社，2009：5－6.

［8］ 丁文祺，冷永刚，范胜波，等.双稳信号的参数调节及恢复［J］.振动、测试与诊断，2010，30（6）：665－670.

Ding Wenqi，Leng Yonggang，Fan Shengbo，et al.Bi－stabe signal recovery with parameter tuning ［J］.Journal of Vibration， Measurement ＆ Diagnosis，2010，30（6）：665－670.（in Chinese）

［9］ 赖志慧，冷永刚，孙建桥，等.基于duffing振子的变尺度微弱特征信号检测方法研究［J］.物理学报，2012，61（5）：31－39.

Lai Zhihui，Leng Yonggang，Sun Jianqiao，et al.Weak characteristic signal detection based on scale transformation of Duffing oscillator［J］.Acta Physica Sinica，2012，61（5）：31－39.（in Chinese）

［10］胥永刚，马海龙，付胜，等.机电设备早期故障微弱信号的非线性检测方法及工程应用［J］.振动工程学报，2011，24（5）：529－538.

Xu Yonggang，Ma Hailong，Fu Sheng，et al.Theory and applications of weak signal non－linear detection method for incipient fault diagnosis of mechanical equipments ［J］.Journal of Vibration Engineering，2011，24（5）：529－538.（in Chinese）

［11］贾启芬，刘习军.机械与结构振动［M］.天津：天津大学出版社，2007：21－22.