基于多目标免疫算法的变刚度悬架的联合优化

史文库，王长新，陈志勇，郭福祥

（1.吉林大学 汽车仿真与控制国家重点实验室，吉林 长春130022；2.南京依维柯汽车有限公司产品工程部，江苏 南京210028）

在汽车悬架开发或改进设计中，由于平顺性和操纵稳定性对悬架的弹性元件刚度和减振器阻尼参数的要求是相互矛盾的，所以经常需要对汽车的前后悬架的刚度和阻尼参数进行匹配优化，以实现某一性能的提升而另一相对性能也能满足常用要求的目的.目前已有多种方法可以对汽车悬架进行多目标优化［1-3］，但几乎都是针对线刚度悬架的.变刚度悬架多目标优化方面的文献很少.况且大多数优化模型是简化模型或者是参数识别的模型.特别是钢板弹簧模型，几乎都是简化模型，模型性能和实际性能有不小的出入.再者车辆轮胎性能对操纵稳定性能有重要的影响，而大多数整车优化模型的轮胎参数也没有都进行实际测试.基于这样的情况，本文首先对样车使用的轮胎进行力学性能测试，以保证优化模型的正确性.同时基于板簧自由状态下形状，采用Beam梁法，建立片数和实际一样多的钢板弹簧模型，优化时采用优化Beam的弹性模量E，来实现刚度的改变.在优化算法选取方面，由于人工免疫算法较进化算法具有很多优异特性，比如收敛速度快，种群多样性好等［4-5］，本文就选择了其中一种常用的人工免疫算法-MISA（multi-objective immune system algorithm）［6-7］.所以本文结合某轻型客车的前后悬架，采用MISA算法对该车的行驶平顺性和操纵稳定性进行平衡优化，然后根据优化结果试制了悬架样件，最后在某汽车试验场进行了悬架优化前后的车辆平顺性和操纵稳定性对比试验.

1 整车多体动力学模型的建立

1.1 轮胎性能参数测试

基于整车的多体动力学模型目标工况仿真与MATLAB人工免疫算法优化计算的联合多目标优化，其优化结果的可信性与所建立多体模型的准确性有很大的关系，而多体模型中轮胎参数对车辆操纵稳定性和平顺性有非常重要的影响［8］.轮胎参数的准确获取需要对其进行力学性能测试，以确保整车模型中的轮胎性能参数与实际轮胎性能参数的一致.文中轮胎试验是在吉林大学汽车工程学院轮胎试验台上进行的，如图1.限于篇幅，只列出稳态侧偏工况和稳态侧倾工况下回正力矩随侧偏角变化关系曲线，如图2和图3，其中Fz代表测试时轮胎垂直加载的载荷值.对试验数据进行全局参数辨识，就可以得到基于魔术公式（Magic Formula）的轮胎模型的参数，然后就可以利用该参数生成属性文件（PAC 2002）以输入到整车的Adams-Car模型中去，为整车前后悬架的联合优化提供可靠的保障.

图1 轮胎力学性能参数测试现场Fig.1 Test of tire mechanical characteristics

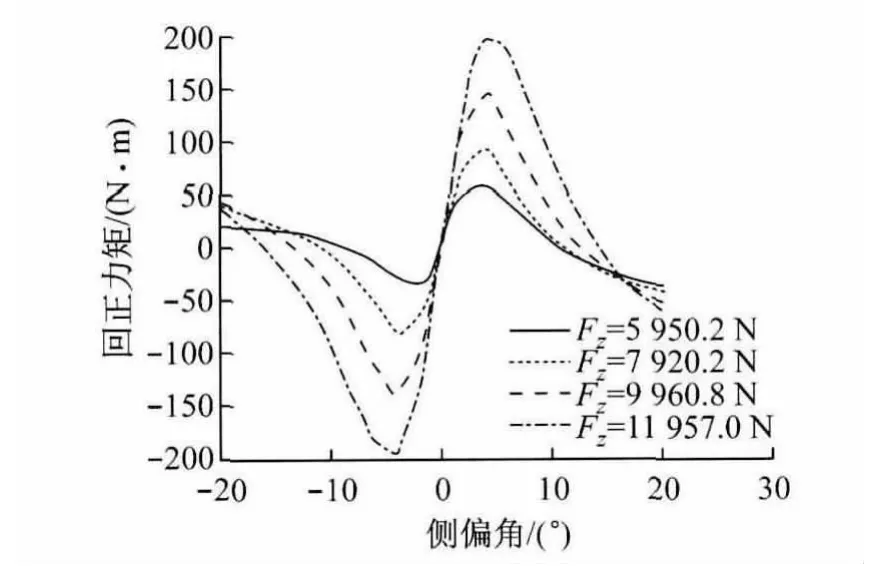
图2 轮胎胎压为475kPa时回正力矩与侧偏角关系曲线Fig.2 Tyre pressure：475kPa，the relationship curves of Mz－α

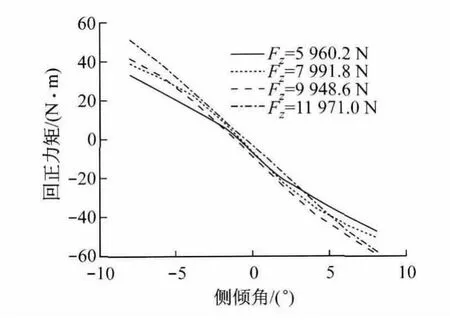
图3 轮胎胎压为475kPa时回正力矩与侧倾角关系曲线Fig.3 Tyre pressure：475kPa，the relationship curves of Mz－γ

1.2 两级变刚度三片式抛物线钢板弹簧后悬架多体模型的建立

某轻型客车为了满足空载和满载下车辆平顺性的要求，采用了两级变刚度三片式抛物线钢板弹簧的后悬架，为了优化该悬架的两级刚度，采用离散Beam梁法建立了该悬架的多体模型，如图4.优化时采用优化板簧Beam梁的弹性模量E，来实现刚度的改变.设置好适当的变化范围，就可以忽略只改变E没有改变钢板弹簧弧高带来的车身变化，这样优化结果可以很接近实际情况，保证了优化方案的可行性.

图4 两级变刚度三片式抛物线钢板弹簧后悬架模型Fig.4 Two-level variable stiffness spring rear suspension model with three parabolic leaves

1.3 整车多体模型的建立

使用Adams-Car软件中的Template模版模块分别建立该车的前、后悬架系统、转向系统、动力系统、制动系统、轮胎和车身的Template，再建立相应的Subsystem，最后组建成整车的多体动力学模型Assembly，如图5.在优化前，对原车进行操纵稳定性和平顺性的试验测试，以此作为模型的验证及优化效果的对比.

图5 整车Adams-Car多体模型Fig.5 Multibody model of the light bus

2 前后悬架参数优化模型

免疫系统是生物信息处理的三大系统之一，人工免疫算法是其衍生的智能算法.它不仅采用交叉、变异算子来维持抗体的多样性，并且通过增加抗体浓度机制来促进和抑制解抗体的产生，增加了解抗体的多样性，确保了该算法能收敛到全局最优解，克服了遗传算法的易早熟收敛的缺点.而多目标免疫系统算法 MISA是Cruz Cortés N.和 Coello C.于2002年提出的，首次将人工免疫系统算法应用于多目标优化问题的求解，并于2003年和2005年对该算法进行了改进，使之具有较好的优化效果［7］.文献［9］在多目标优化方面对比了该算法与遗传算法NASG-Ⅱ，结果表明算法MISA无论是在个体的多样性，还是收敛性上都要比NASG-Ⅱ好.所以本文采用该免疫算法对某轻型客车的前后悬架进行多目标优化，以提高该车的行驶平顺性和操纵稳定性.MISA算法的计算流程见图6.

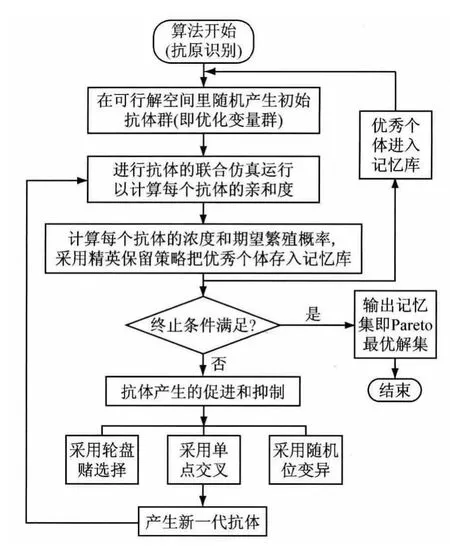
图6 MISA算法流程图Fig.6 Flow chart of MISA

接下来使用MATLAB软件编制MISA算法的优化程序，并联合Adams-Car对某轻型客车的前后悬架进行多目标优化.

前后悬架的垂直刚度和阻尼以及稳定杆的扭转刚度的选取对车辆平顺性和操纵稳定性都具有决定性的作用.所以本文的优化设计变量（即抗体）为：前悬架扭杆的扭转刚度T1，后悬架的一级刚度K1，复合刚度K2，前后横向稳定杆的扭转刚度T2和T3，前后减振器的阻尼特性曲线系数C1和C2.即优化抗体为

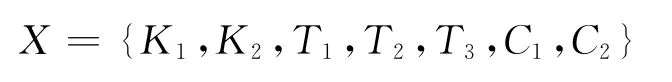
根据该轻型客车常用前后悬架偏频及空满载状态下的偏频确定K1，K2，T1，T2和T3的大致变化范围.C1和C2是在现有阻尼特性曲线的基础上进行优化的一个变量系数，根据该车的实际情况确定二者的变化范围是0.5～2.0.对于目标抗原的选取，主要考虑设计载荷下的车辆性能指标.关于平顺性的目标，需要考虑空载和满载两种车身质量状态，选取在B级路面上80km·h-1匀速行驶时的前后悬架上方车架上对应位置的z向加速度均分根值afz1，afz2，arz1和arz2；关于操纵稳定性的目标，这里使用两种国标试验（GB/T 6323.6—1994和 GB/T 6323.1—1994）下的相关指标.由于稳态回转性能具有操稳性能的“否决权”，所以首先是稳态回转下的车辆所能达到的最大侧向加速度ay1和ay2.为了便于编程优化，这里ay1和ay2取实际测得加速度的绝对值的相反数；其次是基准车速下蛇行试验的平均横摆角速度r1，r2和平均车身侧倾角φ1，φ2.这样整车的优化目标抗原为

式中：下标1表示空载状态下的抗原；下标2表示满载状态下的抗原；w1，w2，w3，w4和w5是权重系数.

根据该优化问题的实际情况增加适当的便于优化处理的约束条件：

（1）根据该车平顺性目标值，要求空满载状态下在B级路面上80km·h-1匀速行驶时的前后测点加权加速度值afz1，afz2，arz1和arz2都小于等于0.55g；

（2）基准车速蛇行试验下，空满载状态下车身侧倾角φ1和φ2都小于等于6°；

（3）考虑车辆的不足转向度是车辆的操稳性能的必要指标，要求空满载状态下横摆角速度增益满足0.18s-1≤r1/δ1≤0.35s-1和0.18s-1≤r2/δ2≤0.35s-1.其中，δ1，δ2分别为空满载下蛇行试验时的方向盘转角.

这样联合仿真优化的大致过程为：由MATLAB程序通过MISA在优化空间里产生初始抗体群，然后依次写入到模型.adm文件，并根据T1的大小和整车质量m1适量调整模型中的参数变量Preload的大小，并写入到模型.adm文件，再调用.acf文件.利用事先编制好的针对该车的驱动文件进行稳态回转、基准车速下的蛇行和80km·h-1、B级路面行驶1 000m的平顺性虚拟试验.随后读取仿真产生的.res文件中数据进行目标函数值计算.再把整车另一质量m2输入到.adm文件中去，重复前述步骤.然后读取.res文件的数据计算得到此状态下的目标函数值，两者组合并再计算此组该抗体的亲和度.这样分别计算出初始抗体群中每个抗体的亲和度，再计算出每个抗体的抗体浓度和期望繁殖概率.根据设置的保优概率，把亲和度最高的若干个抗体直接进入记忆库，再按照期望繁殖概率将优秀抗体存入记忆库.判断是否达到设置的最大代数，若没有达到，则进行抗体群的免疫进化操作（轮盘赌选择、单点交叉和随机位变异），产生新一代抗体群.再循环运行仿真模型，这样直到最大迭代数，最终得到最优抗体记忆集，即得到Pareto非劣解集，并输出Pareto前端.根据其分布情况和实际优化的侧重性从中挑出一两组优化变量，并进行悬架传统设计的常规验算，如符合要求，则可作为设计或改进方案进行下一步的实施.

3 仿真优化及结果

在保证一定的优化效果前提下，为了减少仿真优化时间，文中选取初始抗体数为100，进化代数为30，保优的概率为0.05，交叉概率为0.40，变异概率为0.50.根据优化参数最初值（X0=｛70，135，8.9×104，9×105，7×105，1，1｝）以及实际车辆情况来确定抗体的约束范围：下限Xmin=｛60，100，6×104，6×105，5×105，0.5，0.5｝，上限Xmax=｛80，150，1.2×105，1.2×106，1×106，2，2｝，其单位和Adams-Car模型单位一致，以利于优化计算.经过联合仿真优化可以得到最优抗体记忆集和相应Pareto前端，然后根据Pareto前端分布情况从中选出一组侧重于平顺性的抗体，即优化结果：K1=75N·mm-1，K2=115N·mm-1，T1=7.28×104N·mm·（°）-1，T2=1.0×106N·mm·（°）-1，T3=8.5×105N·mm·（°）-1，C1=1.1，C2=0.8.以此数据进行了车辆悬架常规性能验算，如前后悬架偏频及其比值、前后阻尼比、前后侧倾角刚度及其比值、前后侧倾中心高度、满载下车辆质心位置的变化量、满载下车轮动行程的变化量、满载下车轮定位参数的可调性及可靠性的验算等.若这些都符合设计要求，就可以作为优化方案生产实施.

4 验证试验

根据优化方案进行了悬架样件的加工制造.验证试验包括平顺性试验和操纵稳定性试验.首先验证悬架改进前后车辆平顺性的优化效果，特意选取三种能明显反映悬架平顺性好坏的试验路面工况：小石板路、搓板路和脉冲路况，见图7.

图7 平顺性测试的三种路况Fig.7 Three kinds of road conditions for ride comfort test

试验时车载分空载和满载两种.满载加载是用盛满水的塑料桶假人来模拟乘员的，按照选定常用车速进行平顺性测试.加速度传感器的位置和采用的LMS测试设备见图8.

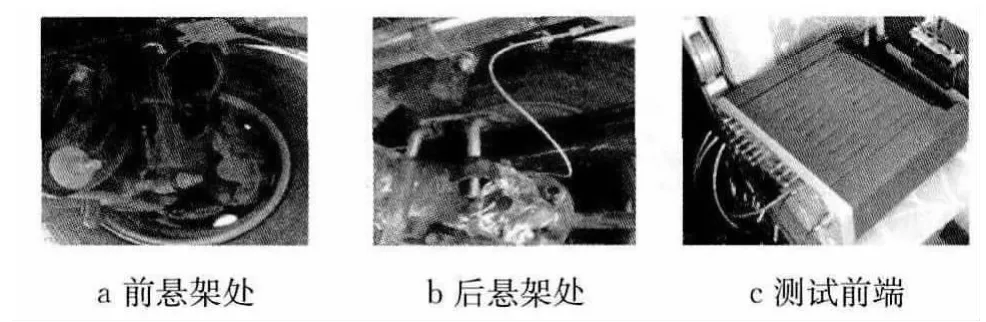
图8 传感器位置和LMS测试前端Fig.8 Sensors locations and LMS test front end

这里评价平顺性的好坏主要是看前后悬架上方车架大梁的z向振动加速度的大小，即计算优化前后的加速度均方根值.限于篇幅，只给出满载小石板路、空载搓板路和空载脉冲路的测试对比结果，分别见表1、表2和表3.表中，前悬上方对应于前悬架上方车架大梁测点处的加速度均方根值，后悬上方对应于后悬架上方车架大梁测点处的加速度均方根值.

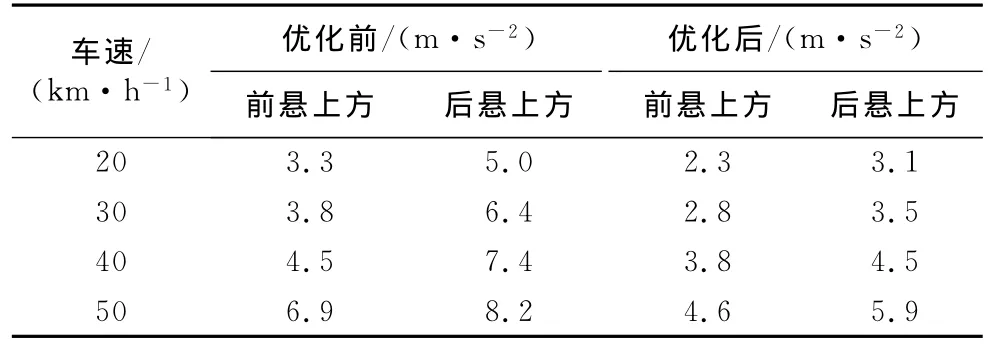
表1 满载小石板路况振动加速度测试结果Tab.1 The results of small stone road acceleration test under full load

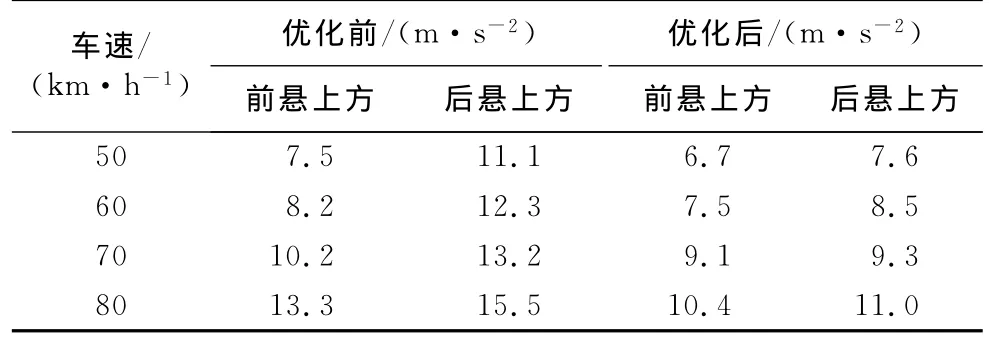
表2 空载搓板路况振动加速度测试结果Tab.2 The results of washboard road acceleration test under empty load

表3 空载脉冲路况振动加速度测试结果Tab.3 The results of pulse road acceleration test under empty load

从表1、表2和表3中数据不难看出，优化后所选的三种试验路面工况上，该车的前后悬架上方的振动大小都较优化前有明显的降低，平均降幅25%左右.由此可以判定优化后该轻型客车的平顺性得到了明显提升.

接下来对优化后该车操纵稳定性能进行试验验证.该试验分为客观和主观试验.客观试验只给出稳态回转试验结果.按照GB/T 6323.6—1994的要求进行试验.图9就是所用操纵稳定试验设备及在某汽车试验场进行的稳态回转试验.

图9 操纵稳定试验设备和稳态回转试验Fig.9 Test and test equipments of handling and stability

图10是满载下稳态回转的对比试验数据结果.从中可以看出，优化后车辆的稳态回转所达到的最大侧向加速度较优化前的有些增加.这可以说明前后悬架优化后该车的操纵稳定性有所提升.

图10 满载稳态回转测试结果Fig.10 The results of steady state circular test

操纵稳定性主观评价试验是由一名国外专业评车师和两名经验丰富的国内评车师分别进行主观评价打分，见图11.打分机制为10分制（10分为满分、6分为及格）.该实验同样分空载和满载两种情况进行.限于篇幅，这里仅给出满载下的主观评价结果，见表4.

图11 操稳主观评价试验Fig.11 The subjective evaluation test of handling and stability

从表4评价数据中可以看出，基本上每项操纵稳定性能指标的得分都有提高，而且国外和国内评车师的评价结果也基本一致.总体平均得分有所增加，这与三位评车师的总体感觉一致，反映了优化后车辆的操纵稳定性能得到了一定的提升.

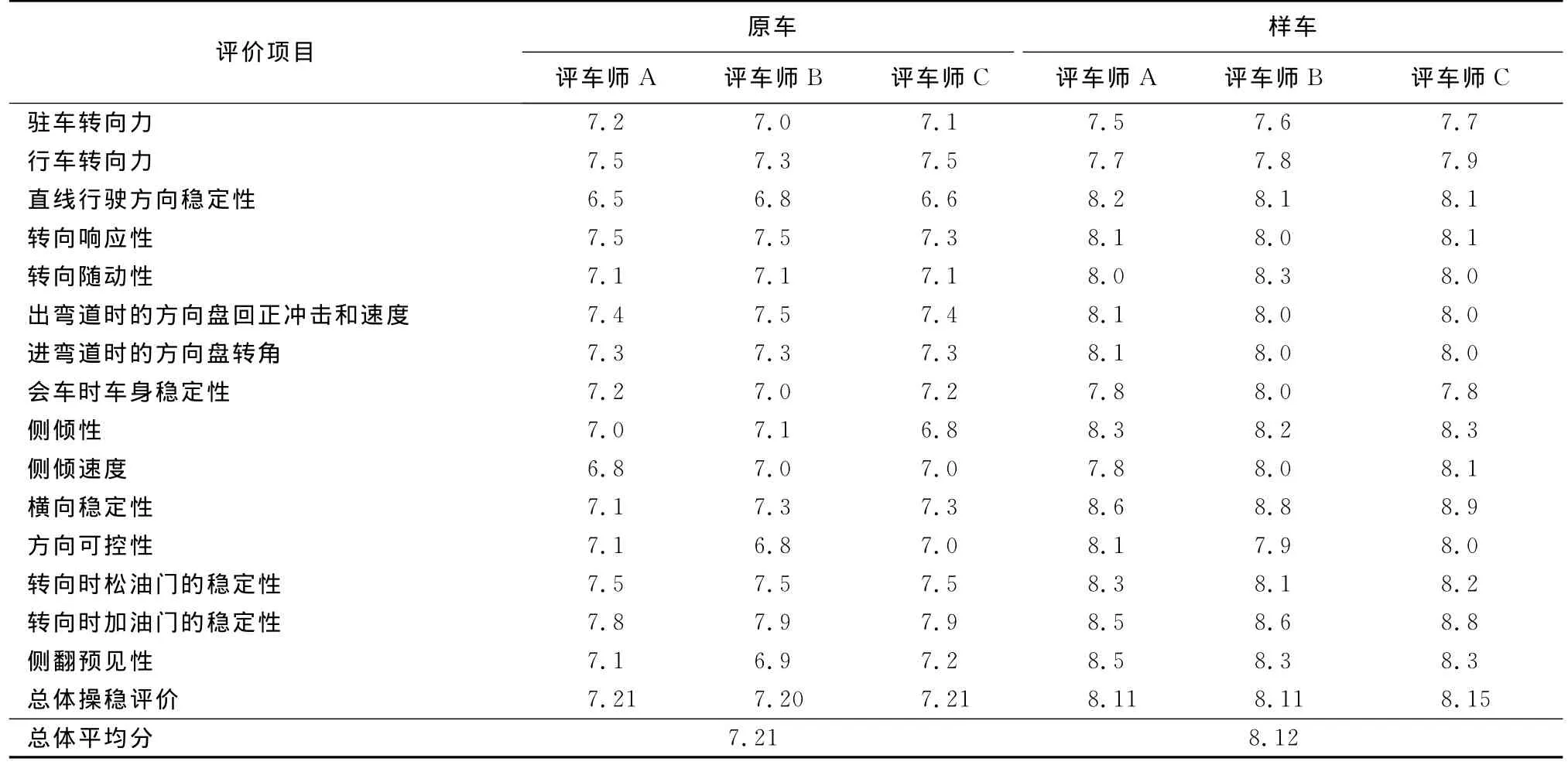
表4 满载下优化前后操纵稳定性能主观评价对比结果Tab.4 The comparison results of the subjective evaluation under full load before and after optimization

5 结语

为了改善某车空载和满载状态下的行驶平顺性和操纵稳定性，本文运用MATLAB和Adams-Car建立了该车的整车多体动力学联合仿真优化模型，采用MISA算法对该车的前后悬架参数进行了多目标匹配优化.优化前特对该车的轮胎进行了力学性能测试，并得到了基于魔术公式的轮胎属性文件.经过联合仿真优化得到了优化方案，并进行样件的试制.最后在某汽车试验场进行样车试验，试验包括小石板路、搓板路和脉冲路三种路况的平顺性对比试验、稳态回转试验和主观操纵稳定评价对比试验.试验结果表明，该车的平顺性有明显提高，操纵稳定性能也有一些提升.这也表明所采用的联合优化方法对于优化车辆的平顺性和操纵稳定性是正确可行的，同时反映了联合优化是汽车CAO技术发展的一种趋势，对汽车底盘的虚拟开发及优化具有一定的指导意义.

［1］ Georgiou Y G， Verros G， Natsiavas S.Multi-objective optimization of quarter-car models with a passive or semi-active suspension system［J］.Vehicle System Dynamics，2007，45（1）：77.

［2］ Gonçalves P C J，Ambrósio A C J.Road vehicle modeling requirements for optimization of ride and handling ［J］.Multibody System Dynamics，2005，13（1）：3.

［3］ Mehrdad N K，Bahram N，Golamhassan P.Multi-objective optimization approach to optimize vehicle ride and handling characteristics［J］.World Academy of Science，Engineering and Technology，2010，38（10）：580.

［4］ Gong M G，Jiao L C，Du H F，etal.Performance assessment of an artifical immune system multiobjective optimizer by two improved metrics ［C］//Proceedings of the Genetic and Evolutionary Computation Conference.Washington D C：IEEE，2005：373-374.

［5］ Karakasis V K，Stafylopatis A.Efficient evolution of accurate classification rules using a combination of gene expression programming and clonal selection［J］.IEEE Transactions on Evolutionary Computation，2008，12（6）：662.

［6］ Cortés N C，Coello C.Multiobjective optimization using ideas from the clonal selection principle［C］//Proceedings of the Genetic and Evolutionary Computation Conference.Berlin：Springer，2003：158-170.

［7］ Coello C，Cortés N C.Solving multiobjective optimization problems using an artificial immune system ［J］.Genetic Programming and Evolvable Machines，2005，6（2）：163.

［8］ 郭孔辉.汽车操纵动力学原理［M］.南京：江苏科学技术出版社，2011.GUO Konghui.Automobile handling dynamics［M］.Nanjing：Jiangsu Science and Technology Press，2011.

［9］ 王鲁，杨婕，熊盛武.一种基于人工免疫系统的多目标优化算法［J］.武汉理工大学学报，2008，30（2）：116.WANG Lu，YANG Jie，XIONG Shengwu.A multi-objective optimization algorithm based on artificial immune system［J］.Journal of Wuhan University of Technology，2008，30（2）：116.