周期性Dresselh au s量子线的开关效应
2014-02-17徐中辉李艳玲黄劲松钟阳万
徐中辉,李艳玲,黄劲松,霍 良,钟阳万
(江西理工大学信息工程学院,江西赣州341000)
周期性Dresselh au s量子线的开关效应
徐中辉,李艳玲,黄劲松,霍 良,钟阳万
(江西理工大学信息工程学院,江西赣州341000)
利用转移矩阵法计算了含周期性Dresselhaus自旋轨道耦合量子线中电子的透射率.结果表明周期性的Dresselhaus自旋轨道耦合会使透射率产生一定宽度的能隙,通过调节自旋轨道耦合强度或者周期单元中两区域的比例长度可以控制能隙的宽度.进一步研究表明当电子入射的能量在能隙范围内的时候,电子被禁止通过,而在能隙外时,电子可以通过,从而实现“关”和“开”的状态.这些效应说明所研究的体系也许能用来设计纳米电子器件.
周期性Dresselhaus量子线;开关效应;自旋轨道耦合
0 引言
低维纳米结构中具有Rashba和Dresselhaus两种自旋轨道耦合,前者是由于量子阱结构的反演不对称性所造成的,后者来自于体材料结构反演非对称性.一般情况下,材料中Rashba自旋轨道耦合强度要比Dresselhaus自旋轨道耦合强度大,同时它的强度大小可以通过电场来控制,所以对Rashba自旋轨道耦合的研究更为普遍[1-3].但是,有些材料[4-6]中Dresselhaus自旋轨道耦合也有比较大的强度,比如Shen等[6]在Dresselhaus自旋轨道耦合作用下得到的自旋霍尔电导与Rashba自旋轨道耦合作用时的大小相等.同时,Sinitsyn等[7]研究了在弱散射的波恩近似下含Rashba和Dresselhaus自旋轨道耦合的顺磁二维电子气中的自旋电流的线性响应电导张量,得到了相似的结论,说明Dresselhaus自旋轨道耦合与Rashba自旋轨道耦合一样非常重要.Jiang等研究了(0 0 1)GaAs量子阱中的Dresselhaus自旋劈裂,结果表明通过结构中的应变可以有效地调节Dresselhaus自旋劈裂,尤其是在某些特定条件下,在窄的GaAs量子阱中通过调节应力可以使Dresselhaus自旋消失,并得到很长的自旋退相位时间.此外,Dmsselhaus强度还可以通过分裂栅极方法调节[9],甚至也可以通过电场来改变其大小[10].因此,很有必要在材料中考虑Dresselhaus的效应.
最近,Gong等[11]研究了一维周期Rashba半导体体量子线中电子自旋输运性质,该装置具有双稳开关效应.同时他们还研究了自旋轨道耦合和磁场的共同作用下的量子线的自旋过滤效应[12]. Xiao等[13]研究了在空间周期性的Rashba和Dresselhaus自旋轨道耦合调制下直量子线的电子输运性质.王瑞琴等[14]利用转移矩阵方法研究了含有Dresselhaus SOC效应的对称性双势垒结构中电子自旋极化共振隧穿的透射系数和隧穿寿命,结果表明自旋简并在Dresselhaus自旋轨道耦合作用下会被消除,并导致透射峰发生自旋劈裂.但是,在以前的大部分工作中很少单独考虑Dresselhaus自旋轨道耦合.文中将利用转移矩阵方法研究周期Dresselhaus量子线的开关效应.
1 模型和计算方法
所研究的周期性Dresselhaus量子线的结构如图1所示,一维理想的直量子线加上空间周期性的Dresselhaus自旋轨道耦合.每个周期性单元包含一个非自旋轨道耦合区间和一个自旋轨道耦合区间,其长度分别为a和b.其中灰色区域代表有Dresselhaus自旋轨道耦合,其它区域没有自旋轨道耦合.从左到右每个区间按照1,2,...,j,-1,j,...,的顺序依次排列,选x轴沿着量子线方向.

图1 含周期性Dresselhaus自旋轨道耦合的理想量子线的结构简图
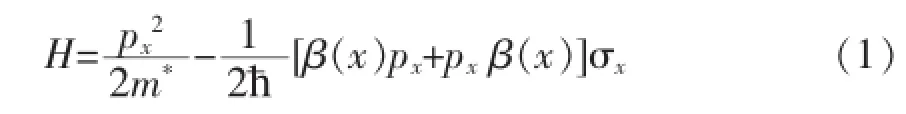
px表示电子在x方向的动量算符且β(x)代表Dresselhaus自旋轨道耦合系数.其中

式(2)中的n=0,1,2,3….
在Dresselhauss半导体量子线中,简并的能带劈裂成两个子带,其本征能量分别为:E+=ħ2k2/2m*+βk和E-=ħ2k2/2m*-βk,其中,E+对应自旋本征态记为|↑〉;E-对应自旋本征态,记为|↓〉.在没有自旋轨道耦合的区域(j为奇数),电子的波函数可以写成:

电子在含Dresselhauss自旋轨道耦合区域(j为偶数)的波函数为:
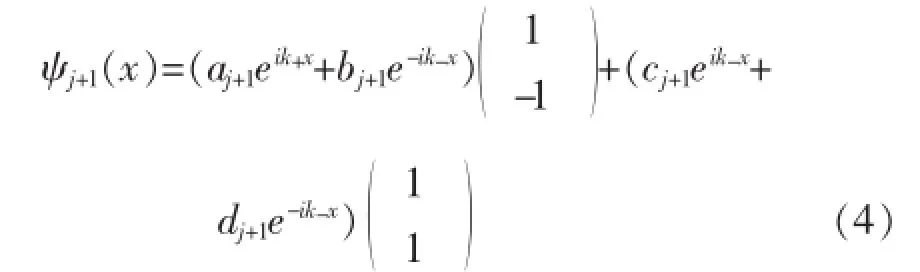
根据量子力学要求,电子波函数须满足以下边界条件[15],即ψj(x)|xj=ψj+1(x)|xj和Fjψj(x)|xj=Fj+1ψj+1·(x)|xj,进一步可以得到以下4个方程:
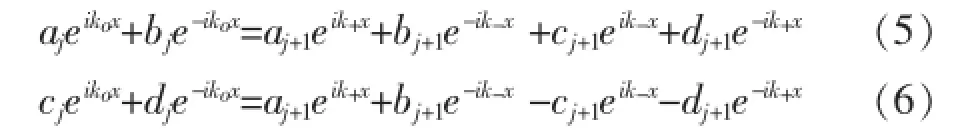

把式(5)、式(6)、式(7)和式(8)合并且写成一个矩阵的形式:


把式(9)简记为:其中只有Lj(xj)和Lj+1(xj)与坐标有关,而Qj和Qj+1与坐标无关.为了计算电子的透射率,把式(10)改写为:
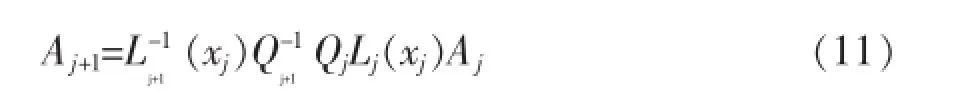
这是一个周期单元中的转移矩阵.如果有多个周期,那么总的转移矩阵为:

从式(12)可以求得电子的透射系数,从而得到它的透射率:
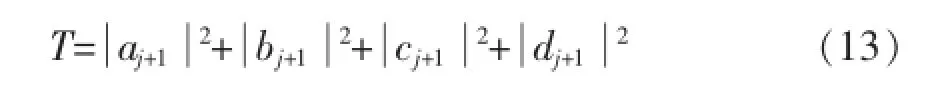
2 数值结果和讨论
量子线由GaAs/AlxGa1-xAs二维电子气加工而成,材料与文献[11,13]中的相同,其中电子的有效质量m*=0.067me,me为自由电子质量.无自旋轨道耦合区域的长度为a=15 nm,含Dresselhaus自旋轨道耦合区域的长度为a=20 nm.周期重复个数为50.

图2 不同Dresselhaus自旋轨道耦合强度下电子透射率随电子入射能量的变化
图2是周期性Dresselhaus量子线在不同自旋轨道耦合强度下,电子的透射率随入射能量的变化.从图2中可以发现,加上Dresselhaus自旋轨道耦合后电子的透射率会出现带隙结构,这是因为给量子线加周期性的Dresselhaus自旋轨道耦合后,有自旋轨道耦合的区域变成了势垒,没有自旋轨道耦合区域变成了势阱,电子相当于在两个不同的一维周期势中运动,因此在透射率中出现了带隙.随着强度β的增大,带隙逐渐变宽并向能量低的方向移动,当Dresselhaus自旋轨道耦合强度β=4.32× 10-11eV·m时,带隙的范围为3.94 meV到4.44 meV,宽度为0.5 meV.在此范围内,电子透射系率为0,当入射电子的能量在此范围内时,它不能通过该量子线.但在能隙外,电子有较高的透射率.由于系统是周期性的,所以透射率也出现了很多周期性的小振荡.如果减小自旋轨道耦合强度,能隙会减小甚至消失,比如当Dresselhaus自旋轨道耦合强度β=1.44×10-11eV·m时,带隙变得很窄了,当耦合强度减小到β=0.50×10-11eV·m时,能隙基本消失了.此外,在能隙范围内,自旋轨道耦合强度的变化对透射率没有很明显的调制.
图3(a)给出了在不同单元长度但是一个单元内两区域长度比例相同的情况下,电子透射率随入射能量的变化.自旋轨道耦合强度为β=4.32× 10-11eV·m.随着一个单元的长度变小,能隙的位置逐渐向能量增大的方向移动,但能隙宽度不变,说明单元长度的变化只影响能隙的位置而不影响它们的宽度.即周期结构的长度可以用来控制能隙的位置.图3(b)是一个单元的长度不变(a+b=35 nm)但是两个区域的长度比例不同时,电子的透射率随着入射能量的变化.随着a:b比值的减小,即含自旋轨道耦合区域的长度增大,左边能隙宽度会减小,比如a:b=1:1时,能隙宽度为0.5 meV;a:b=2:3时,能隙宽度为0.46 meV;a:b=1:4时,能隙宽度为0.28 meV,但右边的能隙宽度增大,比如a:b=2:3时,能隙宽度为0.14 meV,当a:b=1:4时,能隙宽度变为0.34 meV.这是由于左边的能隙由含自旋轨道耦合的区域(势垒)决定的,而右边的能隙由不含自旋轨道耦合的区域(势阱)决定的.这表明自旋轨道耦合强度和两个区域的长度比例都可以用来调制透射率的带隙.即当Dresselhaus自旋轨道耦合强度一定时,调节电子的入射能量,当入射能量处在带隙内时,电子处于“关”的状态,入射能量处在带隙外时,电子处于“开”的状态.同时也可以使入射电子的能量处在能隙范围内,把Dresselhaus自旋轨道耦合强度减小,能隙宽度变小直到消失,电子从“关”的状态变为“开”的状态.
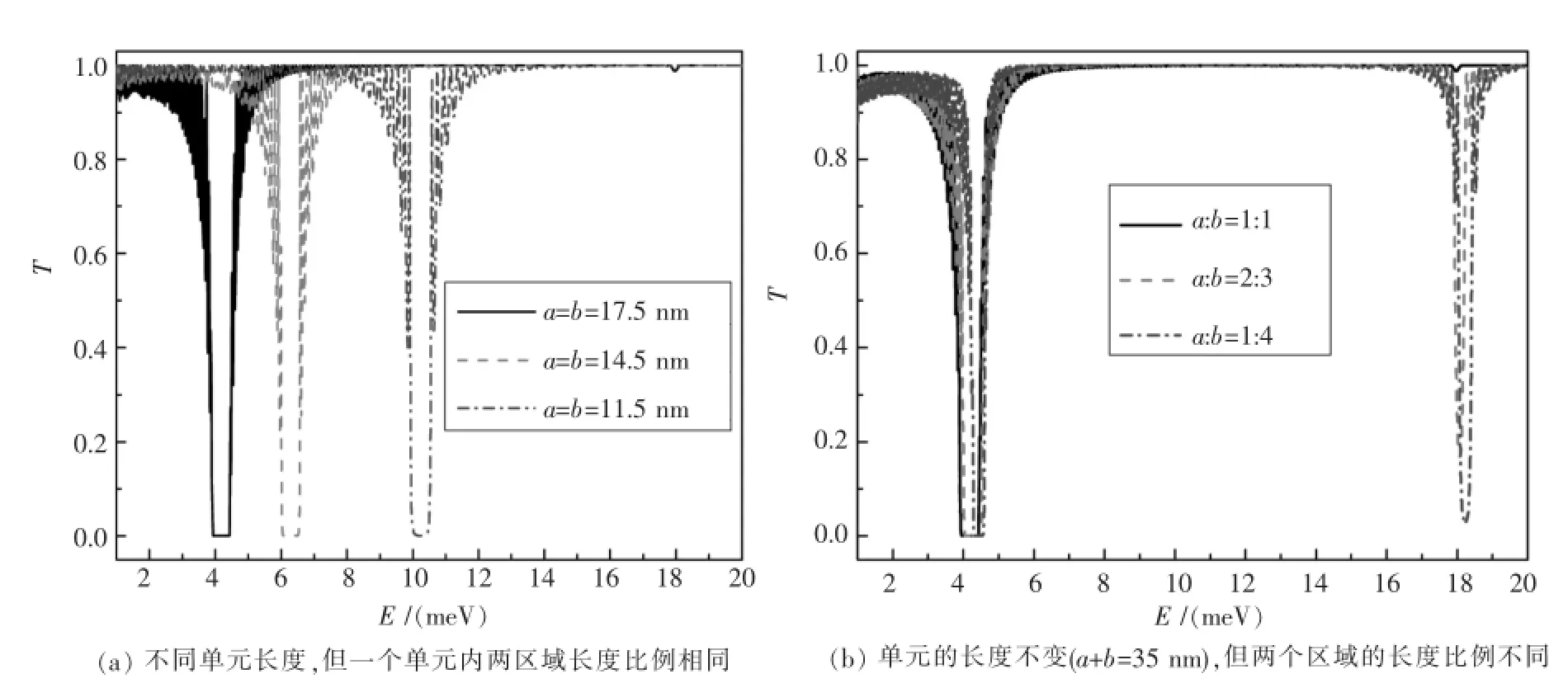
图3 电子透射率随入射能量的变化
由图2可知能隙带宽范围大致为3.94 meV到4.44 meV,为了进一步考察Dresselhaus自旋轨道耦合对电子透射率的调制,图4给出了电子的入射能量处在能隙范围内时,即分别为E=4.1 meV,E=4.2 meV和E=4.3 meV时,电子透射率随Dresselhaus自旋轨道耦合强度的变化.其中a=b= 17.5 nm.从图4可以看出,随着Dresselhaus自旋轨道耦合强度的变化,电子透射率在0和1之间跳跃变化,分别对应于电子处在“关”和“开”的状态,而且在一定Dresselhaus自旋轨道耦合强度范围内,“关”和“开”的状态是稳定的.比如,在电子入射能量E=4.2 meV时,自旋轨道耦合的临界位置在βc=2.0×10-11eV·m.当时,电子透射率为1,当时,电子透射率出现2个小振荡后迅速衰减为0.对于不同的入射能量,Dresselhaus自旋轨道耦合强度具有不同的临界点,电子透射率也有不同的振荡个数,比如E=4.1 meV时,临界点βc=2.10×10-11eV·m,临界点外振荡个数为3个,比如E=4.3 meV时,临界点βc=1.85×10-11eV·m,临界点外振荡个数为1个,即在能隙范围内随着电子入射能量的增大,除临界点外的振荡个数变少,电子透射率更容易从1变成0,这样更有利于“开”和“关”的实现.这是因为在能隙范围内,高能量更接近透射率突变的能量位置,所以振荡自然更少.这个效应有可能在实际的半导体自旋电子器件中用作控制电流的开关.

图4 电子透射率随Dresselhaus自旋轨道耦合强度的变化
3 结论
文中利用转移矩阵法计算了含周期性Dresselhaus自旋轨道耦合量子线中电子的透射率.周期性的Dresselhaus自旋轨道耦合会使透射率产生一定宽度的能隙.当电子入射的能量在能隙范围内的时候,电子被禁止通过,而在能隙外时,电子可以通过,从而实现“关”和“开”的状态.通过调节自旋轨道耦合强度或者周期单元中两区域的比例长度可以控制能隙的宽度.电子以能隙范围内的能量入射时,可以通过调节Dresselhaus自旋轨道耦合强度使电子透射率在0和1之间突变,从而实现电子“关”和“开”的状态.
[1]李艳玲.基于腔-光纤系统制备纠缠和实现远程量子逻辑门的研究进展[J].江西理工大学学报,2011,32(3):73-76.
[2]徐中辉,周详,廖昱博.量子散射的玻恩近似和程函近似[J].江西理工大学学报,2011,32(3):37-56.
[3]徐中辉,肖贤波.含Rashba自旋轨道耦合效应的非均匀量子线的极化输运性质[J].江西理工大学学报,2012,33(3):81-85.
[4]Knap W,Skierbiszewski C,Zduniak A,et al.Weak antilocalization and spin precession in quantum wells[J].Physical Review B,1996, 53(7):3912.
[5]Miller J B,Zumbuhl D M,Marcus C M,et al.Gate-controlled spin-orbit quantum interference effects in lateral transport[J]. Physical Review Letters,2003,90(7):076807.
[6]Shen S Q.Spin Hall effect and Berry phase in two-dimensional electron gas[J].Physical Review B,2004,70(8):081311.
[7]Sinitsyn N A,Hankiewicz E M,Teizer W,et al.Spin H all and spin-diagonal conductivity in the presence of Rashba and Dresselhaus spin-orbit coupling[J].Physical Review B,2004,70 (8):081312.
[8]Jiang L,Wu M W.Control of spin coherence in n-type GaAs quantum wells using strain[J].Physical Review B,2005,72(3): 033311.
[9]Bandyopadhyay S,Cahay M.Alternate spintronic analog of the electro-optic modulator[J].Applied Physics Letters,2004,85(10): 1814-1816.
[10]Schliemann J,Loss D.Anisotropic transport in a two-dimensional electron gas in the presence of spin-orbit coupling[J].Physical Review B,2003,68(16):165311.
[11]Gong S J,Yang Z Q.Ideal switching effect in periodic spin-orbit coupling structures[J].Journal of Physics-condensed Matter, 2007,19:446209.
[12]Gong S J,Yang Z Q.Spin filtering implemented through Rashba spin-orbit coupling and weak magnetic modulations[J].Journal of Applied Physics,2007,102(3):033706.
[13]Xiao X B,Li X M,Chen Y G.Electron transport of a quantum wire with spatially periodic spin–orbit coupling[J].Physica B, 2009,404:4159-4161.
[14]王瑞琴,宫箭,武建,等.对称双势垒量子阱中自旋极化输运的时间特性[J]物理学报,2013,62(8):087303.
[15]Zhang Y T,Guo Y,Li Y C.Persistent spin currents in a quantum ring with multiple arms in the presence of spin-orbit interaction[J].Physical Review B,2005,72(12):125334.
Switch effect of a quantum wire with spatially periodic Dresselhaus spin-orbit coupling
XU Zhong-hui,LI Yan-ling,HUANG Jin-song,HUO Liang,ZHONG Yang-wan
(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
The electron transmission of a Dresselhaus Q uantum W ire(QW)is calculated with the transfer matrix method.The transmission gaps can emerge as a result of the effects of the Dresselhaus S pin-O rbit C oupling(SOC).The width of the gap also can be controlled by the length ratios of each segment or the strengths of SOC.Further studies show that when the incident electrons with energies is within this gap, electrons cannot transmit through the quantum wire;when it is beyond,they can transmit.Hence the switch effectof“ON”and“OFF”can be achieved.Those results may provide an effective way to design a nanometer electronic device.
quantum wire with spatially periodic Dresselhaus;switch effect;spin-orbitcoupling
O469
A
2095-3046(2014)03-0090-05
10.13265/j.cnki.jxlgdxxb.2014.03.017
2014-04-06
国家自然科学基金项目(11365011;11247032);江西省教育厅科技项目(GJJ13383;GJJ13384);江西理工大学科研基金项目(NSFJ2014-G20);江西理工大学教改课题(XJG-2011-100);江西理工大学质量工程项目(XZG-12-08-98)
徐中辉(1982-),男,博士,讲师,主要从事自旋电子学方面的研究,E-mail:longxister@163.com.
